Файл: Обработка сигналов временное представление сигналов временное представление сигналов разложение сигналов по единичным импульсам.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.01.2024
Просмотров: 32
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
k - входного или свертываемого сигнала) располагается по ходу возрастания номеров. Массив второй функции (hn - более короткой, которая обычно называется оператором свертки или оператором фильтра), строится параллельно первому массиву в обратном порядке (по ходу уменьшения номеров первого массива или в режиме обратного времени). Для вычисления yk значение h0 располагается против sk, все значения sk-n перемножаются с расположенными против них значениями hn и суммируются. Результаты суммирования являются выходным значением функции yk, после чего оператор hn сдвигается на один номер k вперед (или функция sk сдвигается ему навстречу) и вычисление повторяется для номера k+1 и т.д.
Свойства свертки. Для свертки характерны следующие свойства:
1. Дистрибутивность:
h(t) * [a(t)+b(t)] = h(t) * a(t)+h(t) * b(t).
2. Коммутативность:
h(t) * a(t) * b(t) = a(t) * b(t) * h(t).
3. Aссоциативность:
[a(t) * b(t)] * h(t) = h(t) * a(t) * b(t).
Преобразование свертки однозначно определяет выходной сигнал y(t) для входного сигнала s(t) при известном значении функции импульсного отклика системы h(t). Обратная задача деконволюции - определение функции s(t) по функциям y(t) и h(t), относится к разряду некорректных потому, что свертка может изменить частотный спектр сигнала y(t) и восстановление функции s(t) становится невозможным.
Любая практическая система должна быть устойчивой, т.е. для сигналов, конечных по энергии или средней мощности, выходные сигналы также должны быть конечными по этим параметрам. Устойчивость обеспечивается при выполнении условия абсолютной интегрируемости импульсного отклика системы:
 |h(t)| dt < .
|h(t)| dt < .
Системы свертки. Свертка выполняется системой (физическим или программным устройством). Физические системы, работающие в реальном времени, вычисляют текущее значение выходного сигнала по всем прошлым значениям входного сигнала и не могут иметь в своем распоряжении будущих значений входного сигнала. Операторы таких систем являются односторонними (каузальными). При сравнении выходного сигнала такой системы со входным нетрудно заметить, что выходной сигнал сдвигается относительно входного сигнала. Для каузальных систем такой "сдвиг по фазе" существует всегда и не может быть исключен.
Входным сигналом программных систем обычно является весь сигнал в целом, записанный в память вычислительного устройства, и при обработке (свертке) входного сигнала в распоряжении системы при вычислении любой текущей точки выходного сигнала имеются как "прошлые" для данной точки, так и "будущие" значения входного сигнала. Это позволяет создавать системы без сдвига фазы выходного сигнала относительно входного. Для создания таких систем может использоваться два способа:
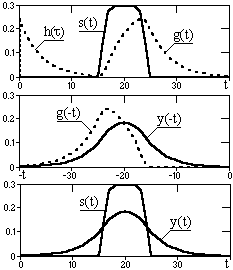
Рис. 2.2.3.
1. Первый способ иллюстрирует рис. 2.2.3. Задается система с односторонним каузальным оператором h(). Входной сигнал s(t) пропускается через систему в обычном порядке и выполняется свертка g(t) = h()*s(t). Затем выходной сигнал g(t) реверсируется ( g(t)=>g(-t), конец сигнала становится его началом в порядке возрастания t) и повторно пропускается через систему, т.е. выполняется свертка y(-t) = h()*g(-t) . Полученный сигнал снова реверсируется (y(-t) => y(t) = h(-)*g(t)) и является окончательным выходным сигналом y(t) системы. Три последние операции (реверс g(t) свертка c h() реверс выходного сигнала) эквивалентны свертке сигнала g(t) с реверсированным откликом системы h(-), и сдвиг по фазе при свертке реверсированного сигнала компенсирует сдвиг по фазе сигнала, полученный при первой свертке. Общий результат операции y(t) = h()*h(-)*s(t) не имеет сдвига по фазе выходного сигнала относительно входного.
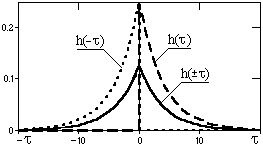
Рис. 2.2.4.
2. Выходной результат y(t) = h()*h(-)*s(t) предыдущей операции позволяет, используя свойство коммутативности свертки, сначала выполнить свертку h()*h(-) = h() и получить один системный оператор h() (см. рис. 2.2.4), обеспечивающий свертку без сдвига фазы. Этот системный оператор является двусторонним и симметричным относительно = 0. Но использование его возможно только для предварительно записанных сигналов, т.к. при выполнении свертки y(t)= h()*s(t-) для отрицательных значений требуются "будущие" значения входного сигнала s(t+). Полученный результат полностью аналогичен первой операции ( рис. 2.2.3).
Приведенное выше формирование двустороннего симметричного оператора свертки имеет чисто познавательный характер. На практике естественным является расчет симметричных двусторонних операторов под требуемые задачи обработки числовых данных (сигналов, зарегистрированных в дискретной числовой форме).
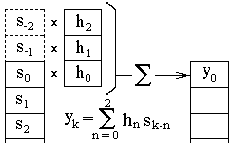
Рис. 2.2.5.
Начальные условия свертки. В начальный момент свертки, при вычислении значений y(ti) для значений ti < max оператора h(), функция оператора, построенная в режиме обратного времени, при >ti "зависает" для значений ti- против отсутствующих значений входной функции. Пример такого зависания оператора дискретной свертки против несуществующих отсчетов s-1 и s-2 входного массива данных при вычислении отсчета у0 приведен на рис. 2.2.5. Зависание исключают либо заданием начальных условий - дополнительных отсчетов, чаще всего нулевых или равных первому отсчету входной функции, либо началом свертки с отсчета входной функции ki = nmax с соответствующим сокращением интервала выходной функции на интервал задания системного оператора. Для симметричных операторов со значениями -n (вперед по времени) такой же момент наступает и в конце входного массива и требует задания конечных условий или сокращения размера выходного сигнала.
Свойства свертки. Для свертки характерны следующие свойства:
1. Дистрибутивность:
h(t) * [a(t)+b(t)] = h(t) * a(t)+h(t) * b(t).
2. Коммутативность:
h(t) * a(t) * b(t) = a(t) * b(t) * h(t).
3. Aссоциативность:
[a(t) * b(t)] * h(t) = h(t) * a(t) * b(t).
Преобразование свертки однозначно определяет выходной сигнал y(t) для входного сигнала s(t) при известном значении функции импульсного отклика системы h(t). Обратная задача деконволюции - определение функции s(t) по функциям y(t) и h(t), относится к разряду некорректных потому, что свертка может изменить частотный спектр сигнала y(t) и восстановление функции s(t) становится невозможным.
Любая практическая система должна быть устойчивой, т.е. для сигналов, конечных по энергии или средней мощности, выходные сигналы также должны быть конечными по этим параметрам. Устойчивость обеспечивается при выполнении условия абсолютной интегрируемости импульсного отклика системы:
Системы свертки. Свертка выполняется системой (физическим или программным устройством). Физические системы, работающие в реальном времени, вычисляют текущее значение выходного сигнала по всем прошлым значениям входного сигнала и не могут иметь в своем распоряжении будущих значений входного сигнала. Операторы таких систем являются односторонними (каузальными). При сравнении выходного сигнала такой системы со входным нетрудно заметить, что выходной сигнал сдвигается относительно входного сигнала. Для каузальных систем такой "сдвиг по фазе" существует всегда и не может быть исключен.
Входным сигналом программных систем обычно является весь сигнал в целом, записанный в память вычислительного устройства, и при обработке (свертке) входного сигнала в распоряжении системы при вычислении любой текущей точки выходного сигнала имеются как "прошлые" для данной точки, так и "будущие" значения входного сигнала. Это позволяет создавать системы без сдвига фазы выходного сигнала относительно входного. Для создания таких систем может использоваться два способа:

Рис. 2.2.3.
1. Первый способ иллюстрирует рис. 2.2.3. Задается система с односторонним каузальным оператором h(). Входной сигнал s(t) пропускается через систему в обычном порядке и выполняется свертка g(t) = h()*s(t). Затем выходной сигнал g(t) реверсируется ( g(t)=>g(-t), конец сигнала становится его началом в порядке возрастания t) и повторно пропускается через систему, т.е. выполняется свертка y(-t) = h()*g(-t) . Полученный сигнал снова реверсируется (y(-t) => y(t) = h(-)*g(t)) и является окончательным выходным сигналом y(t) системы. Три последние операции (реверс g(t) свертка c h() реверс выходного сигнала) эквивалентны свертке сигнала g(t) с реверсированным откликом системы h(-), и сдвиг по фазе при свертке реверсированного сигнала компенсирует сдвиг по фазе сигнала, полученный при первой свертке. Общий результат операции y(t) = h()*h(-)*s(t) не имеет сдвига по фазе выходного сигнала относительно входного.

Рис. 2.2.4.
2. Выходной результат y(t) = h()*h(-)*s(t) предыдущей операции позволяет, используя свойство коммутативности свертки, сначала выполнить свертку h()*h(-) = h() и получить один системный оператор h() (см. рис. 2.2.4), обеспечивающий свертку без сдвига фазы. Этот системный оператор является двусторонним и симметричным относительно = 0. Но использование его возможно только для предварительно записанных сигналов, т.к. при выполнении свертки y(t)= h()*s(t-) для отрицательных значений требуются "будущие" значения входного сигнала s(t+). Полученный результат полностью аналогичен первой операции ( рис. 2.2.3).
Приведенное выше формирование двустороннего симметричного оператора свертки имеет чисто познавательный характер. На практике естественным является расчет симметричных двусторонних операторов под требуемые задачи обработки числовых данных (сигналов, зарегистрированных в дискретной числовой форме).
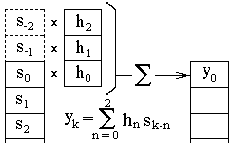
Рис. 2.2.5.
Начальные условия свертки. В начальный момент свертки, при вычислении значений y(ti) для значений ti < max оператора h(), функция оператора, построенная в режиме обратного времени, при >ti "зависает" для значений ti- против отсутствующих значений входной функции. Пример такого зависания оператора дискретной свертки против несуществующих отсчетов s-1 и s-2 входного массива данных при вычислении отсчета у0 приведен на рис. 2.2.5. Зависание исключают либо заданием начальных условий - дополнительных отсчетов, чаще всего нулевых или равных первому отсчету входной функции, либо началом свертки с отсчета входной функции ki = nmax с соответствующим сокращением интервала выходной функции на интервал задания системного оператора. Для симметричных операторов со значениями -n (вперед по времени) такой же момент наступает и в конце входного массива и требует задания конечных условий или сокращения размера выходного сигнала.