ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 47
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ЛАБОРАТОРНАЯ РАБОТА №1
Гидростатическое давление
Цель работы: экспериментальная проверка основного уравнения гидростатики и закона Паскаля.
Теоретические сведения.
В гидростатике рассматривают жидкость, все части которой в некоторой системе координат имеют нулевые скорости. Основным понятием гидростатики является понятие гидростатического давления.
Величина гидростатического давления в случае, когда жидкость находится под действием одной объемной силы – силы тяжести (случай тяжелой покоящейся несжимаемой жидкости) может быть определена по основному уравнению гидростатики:
p=p0+ρ·g·h (1)
где: р – полное или абсолютное давление в точке;
р0 – внешние давление (давление на поверхности жидкости);
ρ – плотность жидкости;
g – ускорение свободного давления;
h – глубина погружения точки в жидкость.
ρ·g·h – весовое давление, обусловленное весом жидкости.
Таким образом, абсолютное давление в точке равно сумме поверхностного и весового давления. Из основного уравнения гидростатики видно, что насколько увеличивается поверхностное давление р0, на столько же должно увеличиться и абсолютное давление в данной точке. Закон Паскаля гласит: приращение давления в любой точке покоящейся жидкости передается во все точки без изменения, если при этом жидкость не начинает двигаться.
Исходя из формулы (1), можно сказать, что расчет абсолютного гидростатического давления сводится к определению абсолютного давления на поверхности жидкости p0 в соответствующих единицах измерения (удельный вес γ или плотность ρ, а также глубина погружения точки h задаются исходными данными).
Абсолютное давление - это давление, отсчитанное от абсолютного нуля (полного вакуума), подобно тому, как отсчитывается температура по шкале Кельвина. В технике промышленных измерений давления отсчет ведут от относительного нуля - атмосферного давления. Давление, выше атмосферного измеряют манометрами, а называют избыточным или манометрическим. Давление, ниже атмосферного (вакуум), измеряют вакуумметрами.
На рис. 1 можно проследить пределы изменения и взаимосвязь абсолютного давления pабс, избыточного pизб, и вакуума pвак.
Рис. 1. Взаимосвязь давлений абсолютного, избыточного и давления вакуума.
р0=ратм+ризб
р0=ратм – рвак
Абсолютное давление при наличии вакуума называют также остаточным давлением.
В открытых сосудах абсолютное давление на поверхности жидкости равно атмосферному давлению.
Применяемые в гидротехнической практике единицы измерения давления и их взаимосвязь следующие:
1 кгс/см2 = 1 ат (техническая атмосфера) = 10000 кгс/м2 =
= 98100 Н/м2 ≈ 0,1 МПа = 1бар
Абсолютное и избыточное давления, выраженные в атмосферах, обозначаются, соответственно, “ат” или “атм” (например, p = 2 ат, p =3 атм и т.п.).
Давление может быть выражено высотой столба жидкости над рассматриваемой точкой. Высота столба жидкости определяется по зависимости:
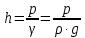(3)Из формулы (3) следует, что одно и то же давление в зависимости от рода жидкости может быть создано столбом различной высоты. Так, техническая атмосфера (1 ат) соответствует 10 м. вод. ст. (при удельном весе воды γ = 1000 кгс/м3 ) = 735,5 мм. рт.ст. (при удельном весе ртути 13600 кгс/м3).
Описание экспериментальной установки: 1 – резервуар установки с жидкостью, 2 – водомерное стекло соединенное непосредственно с резервуаром , 3, 5 – краны на подводящей и сбрасывающей линиях соответственно, предназначены для регулирования уровня жидкости в резервуаре, 4 – кран для удаления («сбрасывания») воздуха при заполнении резервуара жидкостью и таким образом поддержания атмосферного давления над поверхностью жидкости в резервуаре. 6, 7 – манометры для измерения избыточного давления.
Порядок выполнения лабораторной работы:
1. Проверяем, закрыты ли краны 3 и 5 для воды в нижней части резервуара;
2. Открываем на 10 секунд кран 4 для уравновешивания в резервуаре атмосферного давления;
3. Открываем кран 3 для заполнения резервуара водой. Когда показания манометра 7 перестают возрастать (стабилизируются) закрываем кран;
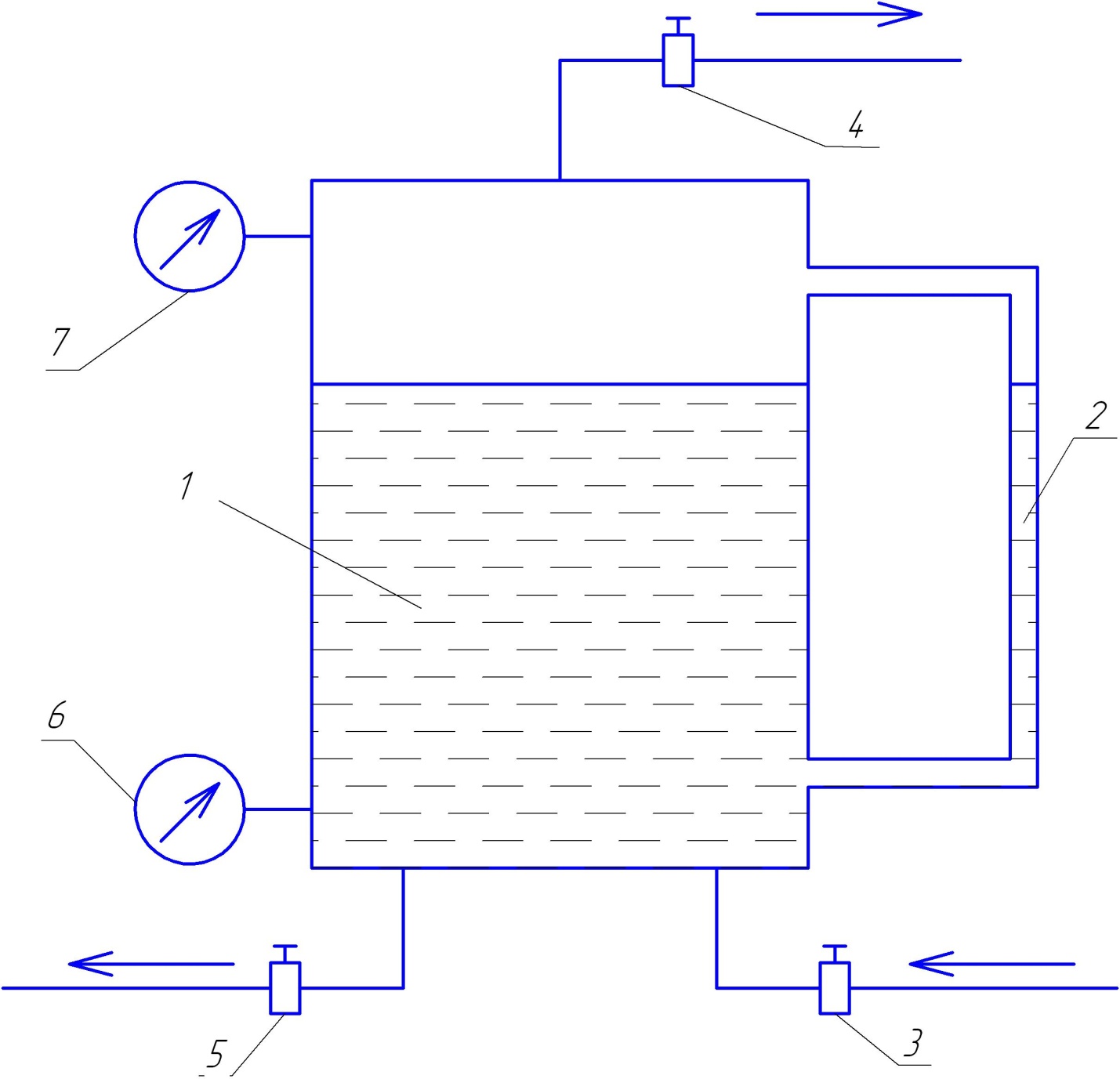
Рис. 2 Схема установки для экспериментального изучения основного уравнения гидростатики.
4. Фиксируем в журнале показания водомерного стекла, а также показания верхнего (7) и нижнего (6) манометров;
5. Открываем воздушный кран 4 на время, необходимое для снижения показания верхнего манометра (7) на 0,1 атм., после чего закрываем его;
6. Повторяем выполнение пунктов 4 и 5 еще 3 раза;
7. Повторно открываем кран 3 для заполнения резервуара водой. Когда показания манометра 7 перестают возрастать (стабилизируются) закрываем кран;
8. Повторяем выполнение пунктов 4 и 5 3 раза;
9. Приводим установку в исходное состояние, для чего открываем воздушный кран 4 и сливаем воду посредством открытия крана 5.
В соответствии с уравнением гидростатики, давления верхнего (рв.м.) и нижнего (рн.м.) манометров должны быть связаны уравнением:
рн.м.=рв.м.+ ρ·g·h
где: h – показания водомерного стекла;
ρ – плотность воды, принимаем ρ=1000 кг/м3;
g – ускорение свободного падения, g=9,81 м/с2;
Порядок обработки полученных результатов:
1. Переводим манометров из атмосфер в паскали из соотношения:
1 атм=9,81·104 Па
2. Определяем расчетное давление на нижнем манометре (ррн.м.) руководствуясь показаниями водомерного стекла и верхнего манометра:
ррн.м.=рв.м.+γ·h
где: γ – удельный вес воды, γ=ρ·g=1000·9,81=9810 Н/м3
3. Определяем абсолютную погрешность измерения давления по формуле:
Δр=ррн.м. – рн.м.
4. Определяем относительную погрешность измерения давления:
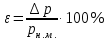
Полученные значения относительной погрешности не превышают 2 %, что является приемлемым результатом и как следствие свидетельствует о применимости основного уравнения гидростатики и закона Паскаля.
| Характеристика | Обозна-чение | Размер-ность | Номер опыта | |||||
| 1 | 2 | 3 | 4 | 5 | 6 | |||
| Показание мерного стекла | h | м | 0,544 | 0,544 | 0,544 | 0,572 | 0,572 | 0,572 |
| Показание верхнего манометра | рв.м. | Па (атм) | 288963(2,95) | 279585(2,85) | 269775(2,75) | 281822(2,87) | 271737(2,77) | 261927(2,67) |
| Показание нижнего манометра | рн.м. | Па (атм) | 294300(3) | 281547(2,87) | 272718(2,78) | 294300(3) | 277623(2,83) | 267813(2,73) |
| Расчетное давле-ние на нижнем манометре | ррн.м. | Па (атм) | 289395(2,946) | 282096(2,88) | 275112(2,8) | 289395(2,946) | 277348(2,827) | 267538(2,727) |
| Абсолютная пог-решность измер-ния давления | Δр | Па (атм) | 4905(0,054) | 549(0,01) | 2394(0,02) | 4905(0,054) | 275(0,003) | 275(0,003) |
| Относительная погрешность измерения давления | ε | % | 1,8 | 0,35 | 0,72 | 1,8 | 1,06 | 1,1 |
ВЫВОД: в результате проведенной лабораторной работы были проведены опыты по подтверждению применимости основного уравнения гидростатики и закона Паскаля в условиях лабораторной установки. Найденная относительная погрешность измерений свидетельствует о правильности проведенных опытов.
ЛАБОРАТОРНАЯ РАБОТА №2
Определение коэффициента расхода водомера Вентури
Цель работы: экспериментальное определение коэффициента расхода водомера Вентури.
Уравнение Даниила Бернулли является основным уравнением гидродинамики. Ниже разбирается это уравнение для установившегося плавно изменяющегося движения жидкости, с помощью которого решаются основные задачи гидродинамики. Введем понятия удельной энергии элементарной струйки и потока жидкости.
У
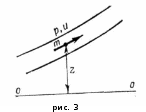дельная энергия элементарной струйки. Напомним, что удельная энергия есть энергия, отнесенная к единице силы тяжести жидкости. Пусть имеем в элементарной струйке частицу массой m, которая обладает некоторой скоростью и, находится под гидродинамическим давлением р, занимает некоторый объем Vи находится от произвольной плоскости сравнения о-о на некоторой высоте z (рис. 3). Масса частицы обладает запасом удельной потенциальной энергии еп, которая складывается из удельных потенциальных энергий положения епол, и давления едав. В самом деле, масса жидкости, поднятая на высоту z, имеет запас потенциальной энергии, равный mgz, где g – ускорение свободного падения. Удельная потенциальная энергия положения равна потенциальной энергии, деленной на силу тяжести жидкости (
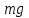).Полная удельная энергия потока Е складывается из удельной потенциальной энергии
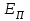и удельной кинетической энергии Ек потока.Для случая установившегося плавно изменяющегося движения жидкости удельная потенциальная энергия во всех точках живого сечения одинакова и равна
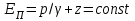.При применении уравнения Д. Бернулли для решения практических задач гидравлики следует помнить два основных условия:
1. уравнение Бернулли может быть применено только для тех живых сечений потока, в которых соблюдаются условия плавно изменяющегося движения. На участках между выбранными сечениями условия плавно изменяющегося движения могут и не соблюдаться;
2. гидродинамическое давление
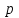и, следовательно, высоту положения zможно относить к любой точке живого сечения, так как 
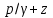для любой точки живого сечения потока при плавно изменяющемся движении есть величина постоянная. Обычно двучлен 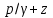удобно отнести для упрощения решения задач к точкам или на свободной поверхности, или на оси потока.Р
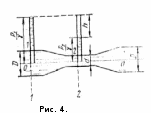азберем применение уравнения Бернулли на примере простейшего водомерного устройства в трубах водомера Вентури (рис. 4.); он представляет собой вставку в основную трубу диаметром D трубы меньшего диаметра d, которая соединена с основной трубой коническими переходами.Водомер Вентури служит для определения расхода жидкости в напорном трубопроводе. Конструктивно он представляет собой круглую трубу переменного сечения с плавным переходом диаметров. Прибор основан на принципе создания в потоке перепада давления путем уменьшения его сечения. Между перепадом давлений и расходом жидкости имеется определенная зависимость, которая и используется для вычисления расхода по измеренному перепаду. Указанная зависимость может быть установлена на основании уравнения Бернулли, записанного для сечений I-I и II-II (рис. 5). Первое сечение намечаем перед входом в сужающее устройство, где наблюдается еще медленно изменяющееся давление; второе сечение проводим в месте наибольшего сжатия потока.
Уравнение Бернулли для данных сечений имеет вид:
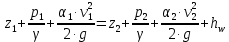(4)где: z1 и z2 – возвышение центров тяжести сечений I-I и II-II над плоскостью сравнения 0-0;
v1 и v2 – средние скорости течения жидкости в первом и втором сечениях соответственно;
α1, α2 – корректировочные коэффициенты кинетической энергии потока соответственно в первом и втором сечениях;
р1 и р2 – гидростатическое давление в центрах тяжести сечений I-I и II-II;
hw – потери напора при движении жидкости от первого до второго сечений;
γ – удельный вес жидкости.