Файл: Курсовая работа Название дисциплины Программирование Тема.docx
Добавлен: 11.01.2024
Просмотров: 78
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Основные данные о работе
| Версия шаблона | 3.1 |
| Вид работы | Курсовая работа |
| Название дисциплины | Программирование |
| Тема | Написать программу, позволяющую выполнять арифметические действия над двоичными, восьмеричными или шестнадцатеричными числами. Систему счисления выбирает пользователь |
| Фамилия студента | |
| Имя студента | |
| Отчество студента | |
| № контракта | |
Содержание
Основные данные о работе 1
Содержание 2
Введение 3
Основная часть 5
1 Системы счисления 5
1.1 Десятичная система счисления 5
1.2 Двоичная система счисления 5
1.3 Восьмеричная система счисления 6
1.4 Шестнадцатиричная система счисления 7
2 Разработка алгоритмов 8
3 Разработка пользовательского интерфейса 12
Заключение 17
Глоссарий 18
Список использованных источников 19
Приложения 20
Введение
Системой счисления называется совокупность приемов наименования и записи чисел. В любой системе счисления для представления чисел выбираются некоторые символы (их называют цифрами), а остальные числа получаются в результате каких-либо операций над цифрами данной системы счисления.
Система называется позиционной, если значение каждой цифры (ее вес) изменяется в зависимости от ее положения (позиции) в последовательности цифр, изображающих число.
Число единиц какого-либо разряда, объединяемых в единицу более старшего разряда, называют основанием позиционной системы счисления. Если количество таких цифр равно
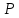 , то система счисления называется -ичной. Основание системы счисления совпадает с количеством цифр, используемых для записи чисел в этой системе счисления.
, то система счисления называется -ичной. Основание системы счисления совпадает с количеством цифр, используемых для записи чисел в этой системе счисления.
Запись произвольного числа
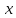 в -ичной позиционной системе счисления основывается на представлении этого числа в виде многочлена
в -ичной позиционной системе счисления основывается на представлении этого числа в виде многочлена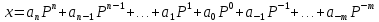
Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и десятичной системе, так как все они основываются на правилах выполнения действий над соответствующими многочленами. При этом нужно только пользоваться теми таблицами сложения и умножения, которые соответствуют данному основанию
 системы счисления.
системы счисления.Тема курсовой работы – «Арифметические операции над числами различных систем счисления».
Цель курсовой работы – разработка программного обеспечения, осуществляющего арифметические действия над числами выбранной системы счисления.
Для достижения цели необходимо решить следующие задачи:
-
Рассмотреть системы счисления; -
Разработать алгоритмы арифметических действий; -
Разработать интерфейс пользователя.
Основная часть
1 Системы счисления
1.1 Десятичная система счисления
Десятичная система счисления пришла из Индии (не позднее VI века нашей эры). Алфавит этой системы: {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} — всего 10 цифр, таким образом, основание системы счисления – 10. Число записывается как комбинация единиц, десятков, сотен, тысяч и так далее. Пример: 1998=8*100 + 9*101 + 9*102 + 1*103.
В этой системе 10 цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, но информацию несет не только цифра, но и место, на котором цифра стоит (то есть ее позиция). Самая правая цифра числа показывает число единиц, вторая справа – число десятков, следующая – число сотен и т.д.
1.2 Двоичная система счисления
Двоичная система счисления была придумана математиками и философами ещё до появления компьютеров (XVII — XIX вв.). Выдающийся математик Лейбниц говорил: "Вычисление с помощью двоек... является для науки основным и порождает новые открытия... При сведении чисел к простейшим началам, каковы 0 и 1, везде появляется чудесный порядок". Позже двоичная система была забыта, и только в 1936 — 1938 годах американский инженер и математик Клод Шеннон нашёл замечательные применения двоичной системы при конструировании электронных схем.
В двоичной системе числа записываются с помощью двух цифр: 0,1.
Перевод десятичного числа в двоичное число:
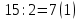
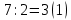
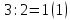
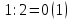
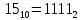
Существуют системы счисления, родственные двоичной. При работе с компьютерами иногда приходится иметь дело с двоичными числами, так как двоичные числа заложены в конструкцию компьютера. Двоичная система удобна для компьютера, но неудобна для человека — слишком длинные числа неудобно записывать и запоминать. На помощь приходят системы счисления, родственные двоичной — восьмеричная и шестнадцатеричная.
1.3 Восьмеричная система счисления
В восьмеричной системе числа записываются с помощью восьми цифр: 0,1,2,3,4,5,6,7, а сама восьмерка числом 10. Удобство восьмеричной системы счисления заключается в том, что переход от восьмеричной к двоичной очень прост: достаточно каждую восьмеричную цифру заменить ее двоичным представлением (двоичной триадой), в соответствии с приведенной ниже таблицей.
| восьмеричная система счисления | | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| двоичная система счисления | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
Например, 5028 = 101 000 0102
Достаточно прост и обратный переход от двоичной с/с к восьмеричной. Для этого в двоичной записи числа нужно выделить триады (влево и вправо от десятичной точки) и заменить каждую триаду соответствующей восьмеричной цифрой. В случае необходимости неполные триады дополняются нулями.
Например, 1 111 1102 = 001 111 1102 = 1768
1.4 Шестнадцатиричная система счисления
Шестнадцатеричная система счисления, так же как восьмеричная, широко используется в компьютерной науке из-за простоты перевода в нее двоичных чисел. В случае шестнадцатеричной записи числа получаются более компактными.
В качестве алфавита шестнадцатеричной системы счисления используются цифры от 0 до 9 и шесть первых латинских букв – A, B, C, D, E, F. При переводе в десятичную систему буквы заменяются числами 10, 11, 12, 13, 14, 15 соответственно.
При переводе двоичного числа в шестнадцатеричное, первое разбивается на группы по четыре разряда, начиная с конца. В случае, если количество разрядов не кратно четырем, первая четверка дописывается нулями впереди. Каждой четверке соответствует одноразрядное число шестнадцатеричной системы счисления.
| Двоичная система счисления | Шестнадцатиричная система счисления |
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
0100 1100 0101 = 4 C 5
2 Разработка алгоритмов
Для выполнения арифметических действий над числами будет использоваться следующий алгоритм:
1. Проверка введенных чисел на принадлежность к выбранной системе счисления;
2. Перевод введенных чисел в десятичную систему;
3. Выполнение арифметических действий над десятичными числами (+, -, *, /);
4. Перевод результата в выбранную систему счисления и вывод на экран.
Функция определения принадлежности введенного числа выбранной системе счисления:
function CheckInput(ch:String;r:Byte):Boolean;
var
i,j:Byte;
res:Boolean;
begin
CheckInput:=True;
For i:=1 to Length(ch) do
begin
res:=False;
For j:=1 to r do
if ch[i]= digit[j] then
begin
res:=True;
break;
end;
if (res=False) and (ch[i]<>',') then
begin
CheckInput:=False;
break;
end;
end;
end;
Где ch – строковое значение введенного числа, r – основание системы счисления.
Функция перевода из любой системы счисления в десятичную систему целого числа:
function ToDec(var ss: string; cc: byte): integer;
var
i, n, sum: integer;
begin
sum := 0;
n := length(ss);
for i := 1 to n do
begin
dec(n);
sum := sum + round((pos(ss[i], digit) - 1) * exp(ln(cc) * n));
end;
ToDec := sum;
end;
Где ss – строковое значение введенного числа, cc – основание системы счисления.
Функция перевода из десятичной системы счисления в любую систему счисления целого числа:
function Cel(d: real; c: integer): string;
var
s: string;
n2: integer;
begin
n2 := round(int(d));
s := '';
repeat
s := ((digit[n2 mod c + 1]) + s);
n2 := n2 div c;
until (n2 = 0);
Cel := s;
end;
Где d – строковое значение введенного числа, c – основание системы счисления.
Процедура разделения дробного числа на целое и остаток:
procedure Del(var ss: string);
var
i: integer;
begin
ind := 0;
s2 := '';
for i := 1 to length(ss) do
if ss[i] in [',', '.'] then
begin
ind := i;
break
end
else
s2 := s2 + ss[i];
s3 := '';
if ind <> 0 then
begin
delete(s, 1, ind);
s3 := ss;
end;
end;
Функция перевода дробной части из десятичной системы счислению в любую систему:
function Drob(var d: real; t, c: integer): string;
var
s: string;
l2, k: real;
i: integer;
begin
k := d - int(d);
s := '';
i := 0;
if t <> 0 then begin
repeat
l2 := k * c;
k := frac(l2);
s := s + digit[round(int(l2)) + 1];
inc(i);
until i = t;
end
else
s := '0';
Drob := s;
end;
Функция перевода дробной части из любой системы счислению в десятичную систему:
function drob2(ss: string; c: integer): real;
var
i: integer;
sum: real;
begin
sum:=0;
for i := 1 to length(ss) do
sum := sum + (pos(ss[i], digit) - 1) * exp(ln(c) * -i);
drob2 := sum;
end;
3 Разработка пользовательского интерфейса
Для удобства работы пользователя с программой разработаем пользовательский интерфейс.
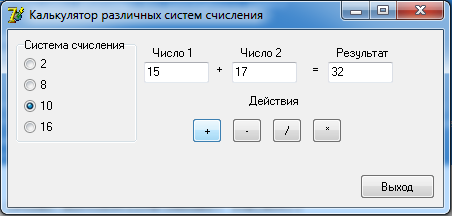
На форме слева расположим блок для выбора системы счисления. Далее поля для ввода чисел и поле для вывода результата.
Под полями ввода разместим кнопки с обозначениями арифметических действий. При нажатии на них будет формироваться и выводится результат.
В правом нижнем углу разместим кнопку «Выход» для завершения работы с программой.
Интерфейс пользователя представлен на рисунке 1.
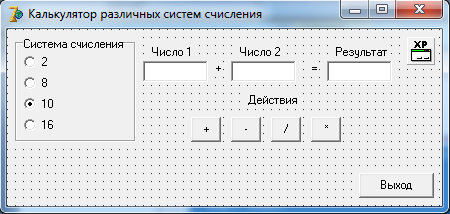
Рисунок 1. Интерфейс пользователя
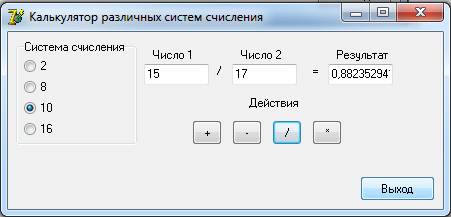
Проведем тестирование разработанного программного обеспечения.