4. ИЗУЧЕНИЕ МАГНИТНОГО ПОЛЯ ТОКА
Цель работы – изучение магнитного поля, создаваемого током текущим по прямоугольной рамке. Измерение с помощью индукционного датчика, соединенного с ламповым вольтметром, магнитного поля Н нижнего участка этой рамки при различных расстояниях от него. Построение графика зависимости магнитного поля от расстояния и сравнение его с теоретическим, полученным на основании закона Био-Савара-Лапласа.
Общие сведения.
П 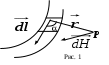роводник, по которому протекает электрический ток, создает магнитное поле. Магнитное поле характеризуется вектором напряженности H (рис.1), который можно вычислить по формуле

H = dH.

Cогласно закону Био-Савара-Лапласа,

,

где I – сила тока в проводнике, dl – вектор, имеющий длину элементарного отрезка проводника и направленный по направлению тока, r – радиус вектор, соединяющий элемент с рассматриваемой точкой P.

Р 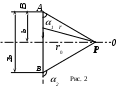ассмотрим магнитное поле, создаваемое прямолинейным проводником с током конечной длины (рис.2). Отдельные элементарные участки этого проводника создают поля dH, направленные в одну сторону (перпендикулярно плоскости чертежа), поэтому напряженность магнитного поля в точке P может быть найдена интегрированием:



Имеем l= r_o сtg, так что Кроме того, Поэтому



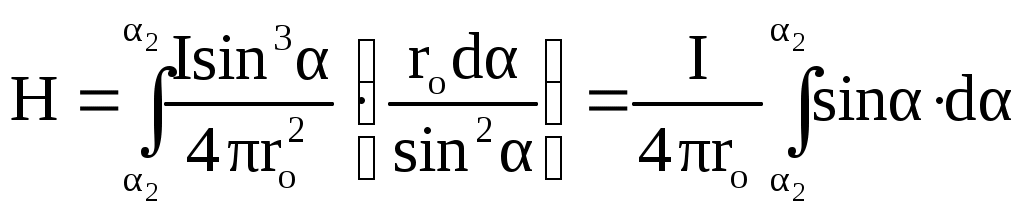
После интегрирования получим
, (1)

где r_o – кратчайшее расстояние от точки P до проводника с током, ₁ и ₂ - углы между крайними элементами проводника и соответствующими радиус-векторами PA и PB.

---

Если определять напряженность в точках, расположенных на перпендикуляре, восстановленном к середине проводника, то cos₂ = cos(180 -₁) = - cos₁ и, следовательно,

(cos₁ - cos₂) = 2cos₁ = . (2)

С учетом выражения (2) формулу (1) можно записать в виде

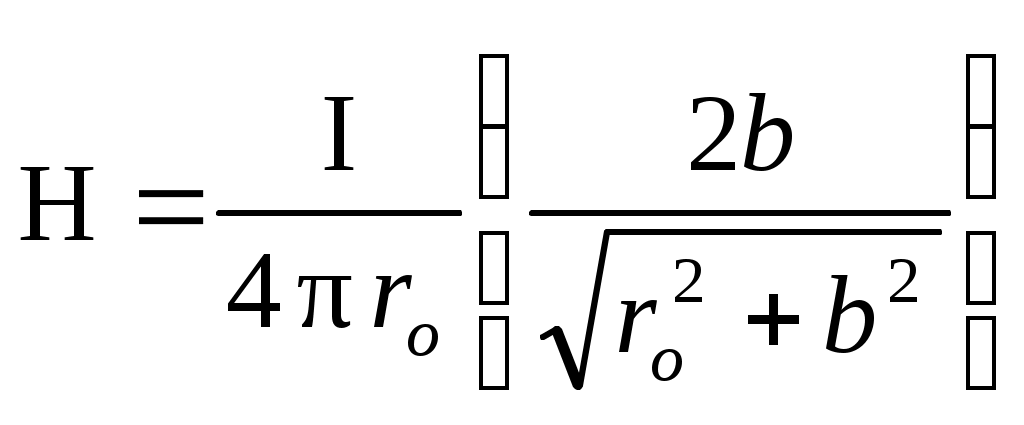. (3)

Д 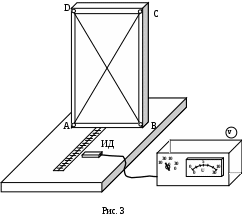ля исследования зависимости магнитного поля прямолинейного тока от расстояния до проводника применяется следующий метод. Прямоугольная, вытянутая по вертикали рамка ABCD (рис. 3) присоединяется к генератору переменной ЭДС. По рамке течёт переменный ток, изменяющийся с течением времени t, следующим образом:

,

где I_о – амплитудное (максимальное) значение тока в цепи;  - угловая частота переменного тока.

Вокруг проводника создаётся переменное магнитное поле напряжённостью:

,

где Н_о – амплитудное значение напряжённости.

Маленькая плоская катушка – индукционный датчик (ИД), содержащий N витков, помещается в точке P поля так, чтобы её центр совпал с этой точкой. По законам электромагнитной индукции в катушке возникает ЭДС:

,

где Ф – магнитный поток, пронизывающий каждый виток катушки.

Известно, что:

,

где _о – магнитная постоянная;  - магнитная проницаемость среды, в которой создано магнитное поле, в нашем случае =1, так как поле создано в воздухе; S – площадь измерительной катушки ИД.

Поэтому можно записать:

(4)

Обозначив

(5)

получим

(6)

---

Равенство (5) показывает, что _о пропорционально Н_о. Следовательно, измерив _о, можно рассчитать значение Н_о в любой точке поля. Так как (здесь _эф – действующее значение ЭДС), то:

. (7)
Порядок выполнения эксперимента.
Рамка ABCD закреплена вертикально и изучаемый участок AB параллелен плоскости стола (рис. 3). Векторы напряженности магнитного поля, создаваемого сторонами AD и BC, параллельны плоскости стола и индукционный датчик изменения потока этих векторов не фиксирует. Напряженностью магнитного поля, созданного током, текущим через участок DC, можно пренебречь.

Последовательность действий при измерении следующая:

1. 
   Включить ламповый вольтметр и подождать несколько минут, пока он прогреется.
   

На лабораторном столе перпендикулярно к нижнему участку рамки AB нанесена шкала расстояний. Индукционный датчик ИД поместить плоской стороной к поверхности стола на расстоянии x от рамки (по шкале расстояний). Оценить максимальную ошибку x. Отодвигая датчик от рамки, через каждые 2 см измерить величину напряжения E_эф.

2. 
   Чтобы измерить напряжение E_эф поставьте переключатель диапазонов вольтметра в положение 300 mВ. Вся шкала в этом случае соответствует 300 mВ. Снять измерения по нижней шкале прибора. Погрешность этого измерения E определить по общему правилу оценки погрешностей электрических измерений. Класс точности определить по частоте переменного тока. По мере необходимости, при уменьшении E_эф, изменить пределы измерения вольтметра.
   
3. 
   Результаты измерений оформить в виде таблицы 1.
   

Таблица 1.

х, м	х, м	ro, м	 ro, м	Еэф, В	Еэф, В	Н, А/м
0
0,02
0,04
…

---

Обработка результатов измерения
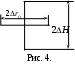Вычислить расстояние от датчика до середины участка AB r_o = x + d/2, где d - ширина участка AB рамки. Для полученных значений r_o построить график зависимости Н(r_o).

Построить график зависимости Н(r_o), вычисляя Н по формуле (7), получить формулу погрешности Н и вычислить Н для всех точек. Каждую точку графика Н(r_o) окружить крестом, вертикальный размер которого должен соответствовать 2Н, горизонтальный – 2r₀ (рис. 4).

Содержание отчета

1. 
   Цель работы.
   
2. 
   Схема установки.
   
3. 
   Основные формулы. Таблица результатов измерений.
   
4. 
   Вывод формул экспериментальной погрешности H. Расчет H для наибольшего и наименьшего значений r_o.
   
5. 
   Графики зависимостей H(r_o).
   

Контрольные вопросы

1. 
   В чем заключается закон Био-Савара-Лапласа и как его применять при расчете магнитных полей проводников с током?
   
2. 
   Как определяется направление вектора в законе Био-Савара-Лапласа?
   
3. 
   Почему индуктивный датчик, лежащий на столе, не регистрирует магнитные поля, создаваемые участками и принизывающий индукционный датчик, расположенный на столе?
   
4. 
   В чем состоит закон электромагнитной индукции?
   

---

Смотрите также файлы

• Туалетные принадлежности с 09. 11. 19 по 13. 11. 19.docx

• Пустота она полна Пустота она полна Пустота она полна.docx

• Протокол 1 моу чеботаевская сш от 22 августа 2022 г. Тимонин А. В. Приказ 104 от 22. 08. 2022 г. Положение.pdf

• Управление персоналом одна из сфер менеджмента, где этика управления является основой предупреждения и разрешения как производственных, так и социальных конфликтов.docx

• Особенности органических веществ. Классификация органических соединений. Демонстрация 10Модели метана, этана, этена, этина, этанола, этаналя, этановой кислоты, глюкозы, аминоэтановой кислоты.pptx