Файл: Сборник контрольных рабор по геометрии 10 класс Пояснительная записка.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 48
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Распределение заданий по содержанию и уровню сложности
| Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
| Параллельные плоскости | №1,2 | №4 | №5 | 80% |
| Параллельное проектирование | | №3 | | 20% |
| Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
| 1 | Признак параллельности плоскостей | Выполнение чертежа по условию задачи | 1 балл | 3 балла |
| Применение признака параллельности плоскостей | 1 балл | |||
| Оформление решения задачи | 1 балл | |||
| 2 | Признак параллельности плоскостей | Применение признака параллельности плоскостей | 1 балл | 3 балла |
| Оформление решения задачи | 2 балла | |||
| 3 | Параллельное проектирование | Знание и применение свойств параллельного проектирования | 3 балла | 5 баллов |
| Выполнение построения | 1 балл | |||
| Оформление решения задачи | 1 балл | |||
| 4 | Свойства параллельных плоскостей | Выполнение чертежа по условию задачи | 1 балл | 5 баллов |
| Применение свойств параллельных плоскостей | 1 балл | |||
| Свойство углов | 1 балл | |||
| Оформление решения задачи | 2 балла | |||
| 5 | Квадрат. Признаки и свойства | Выполнение чертежа по условию задачи | 2 балла | 5 баллов |
| Подобие треугольников | 2 балла | |||
| Оформление решения задачи | 1 балл |
Критерии оценивания:
1-10 баллов – «2»
11-15 баллов – «3»
16-19 баллов – «4»
20-21 балл – «5»
Контрольная работа №4 10 класс.
Тема: «Перпендикулярность прямых, прямой и плоскости».
Цель: проверить уровень усвоения ГОСО:
- знания и умения применять при решении задач определение, признаки и свойства перпендикулярных прямых, прямой и плоскости;
-знания и умения применять при решении задач теорему о трех перпендикулярах;
- умение выполнять чертежи по условию задачи;
- умение оформлять решение задачи.
| I вариант. |
| 1. Дано: АВ ┴ α, CD ┴ α, AB=CD.Определить вид четырехугольника ABCD. 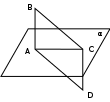 2. Дан куб ABCDA1B1C1D1. Докажите что: AD ┴ (DCC1). 3. Из точки S к плоскости α проведены перпендикуляр SO и наклонные SA и SB. Найдите SB, если SA=20 см, АО=16 см, ОВ=5см. 4. Точка S не лежит в плоскости прямоугольника ABCD и равноудалена от его вершин. Найдите расстояния от точки S до вершин прямоугольника, если расстояние от точки S до плоскости АВС равно 24 см, АВ=12 см, ВС=16 см. 5. Из точки к плоскости прямоугольного треугольника с катетами 15 и 20 см проведен перпендикуляр длинной 16 см. Основание перпендикуляра, вершина прямого угла треугольника. Найдите расстояние от данной точки до гипотенузы. |
| II вариант. |
| 1 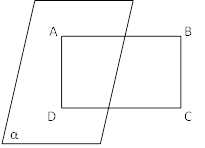 .Дано: ABCD параллелограмм .Дано: ABCD параллелограмм АВ ┴ α, АС=8. Найти BD 2. Дан куб ABCDA1B1C1D1. Докажите что: BB1 ┴ (ABC). 3. Из точки S к плоскости α проведены перпендикуляр SO и наклонные SA и SB. Найдите АО, если SB=17 см, ОВ=15 см, SA=10 см. 4. Точка S не лежит в плоскости прямоугольника ABCD и равноудалена от его вершин. Найдите расстояние от точки S до плоскости прямоугольника, если стороны прямоугольника 6 и 8 см, а SA=13 см. 5. Из точки, к плоскости треугольника со сторонами 13 см, 14 см, 15 См проведен перпендикуляр, основание которого вершина угла противоположная стороне 14 см. Расстояние от данной точки до этой стороны равно 20 см. Найдите расстояние от точки, до плоскости треугольника. |
Распределение заданий по содержанию и уровню сложности
| Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
| Перпендикулярные прямые | №1 | | | 20% |
| Перпендикулярные прямая и плоскость | № 2 | | | 20% |
| Перпендикуляр и наклонная | | №3, 4 | | 40% |
| Теорема о трех перпендикулярах | | | №5 | 20% |
| Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
| 1 | Свойства перпен-дикулярных прямых. | Применение свойств прямых перпендикулярных плоскости. | 2 балла | 3 балла |
| Оформление решения задачи. | 1 балл | |||
| 2 | Признак перпендикулярности прямой и плоскости. | Применение признака перпендикулярности. | 1 балл | 3 балла |
| Оформление решения задачи. | 2 балла | |||
| 3 | Перпендикуляр и наклонная. | Выполнение чертежа по условию задачи. | 1 балл | 5 баллов |
| Вычисления. | 1 балл | |||
| Оформление решения задачи. | 3 балла | |||
| 4 | Перпендикуляр и наклонная. | Выполнение чертежа по условию задачи. | 1 балл | 5 баллов |
| Применение свойства точки равноудаленной от вершин прямоугольника. | 1 балл | |||
| Вычисление. | 1 балл | |||
| Оформление решения задачи | 2 балла | |||
| 5 | Теорема о трех перпендикулярах. | Выполнение чертежа по условию задачи. | 2 балла | 5 баллов |
| Знание и применение ТТП. | 2 балла | |||
| Оформление решения задачи. | 1 балл |
Критерии оценивания:
1-10 баллов – «2»
11-15 баллов – «3»
16-19 баллов – «4»
20-21 балл – «5»
Контрольная работа №5 10 класс.
Тема: «Перпендикулярность плоскостей».
Цель: проверить уровень усвоения ГОСО:
- знания и умения применять при решении задач определение, признаки и свойства перпендикулярных плоскостей;
-умения определять расстояние между скрещивающимися прямыми, углы между плоскостями
- умение выполнять чертежи по условию задачи;
- умение оформлять решение задачи.
| I вариант. |
| 1. Прямая SA проходит через вершину прямоугольника ABCD и перпендикулярна его сторонам АВ и AD. Докажите перпендикулярность плоскостей: SAD и АВС. 2. Ребро куба ABCDA1B1C1D1 равно 4. Найдите расстояние между прямыми АВ и СС1. 3. Плоскости равнобедренных треугольников ABD и АВС с общим основанием перпендикулярны. Найдите CD, если AD= 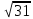 см, АВ=6 см, АСВ=60ᴼ. см, АВ=6 см, АСВ=60ᴼ. 4. Перпендикулярные плоскости α и β пересекаются по прямой L. Отрезки ОА и ОВ лежащие на плоскостях α и β соответственно, перпендикулярны прямой L, а их общий конец – точка О лежит на прямой L. Найдите АВ, если ОА=20 см, ОВ:АВ=12:13 5. Через вершину В равнобедренного треугольника АВС проведена плоскость, параллельная основанию АС. Найдите углы наклона боковых сторон к этой плоскости, если основание АС=12 см и удалено от данной плоскости на 5 см, а площадь треугольника равна 48 см2. |
| II вариант. |
| 1. Прямая SA проходит через вершину прямоугольника ABCD и перпендикулярна его сторонам АВ и AD. Докажите перпендикулярность плоскостей: SAB и АВС. 2. Ребро куба ABCDA1B1C1D1 равно 4. Найдите расстояние между прямыми СС1 и В1D1. 3.Плоскости равнобедренных треугольников ABD и АВС с общим основанием перпендикулярны. Найдите CD, если AD=10 см, AВ=16 см, САВ=45ᴼ. 4. Перпендикулярные плоскости α и β пересекаются по прямой L. Отрезки ОА и ОВ лежащие на плоскостях α и β соответственно, перпендикулярны прямой L, а их общий конец – точка О лежит на прямой L. Найдите АВ и ОВ, если АВ=40 см, ОА:ОВ=3:4 5. Через вершину А ромба ABCD проведена плоскость, параллельная диагонали BD. Найдите углы наклона сторон АВ и AD к этой плоскости, если диагональ BD равна 16 см и удалена от данной плоскости на 5 см, а площадь ромба равна 96 см2. |
Распределение заданий по содержанию и уровню сложности
| Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
| Перпендикулярные плоскости | №1 | №3,4 | | 60% |
| Расстояние между скрещивающимися прямыми | №2 | | | 20% |
| Угол между прямой и плоскостью | | | №5 | 20% |
| Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
| 1 | Признак перпендикулярности плоскостей | Выполнение чертежа по условию задачи | 1 балл | 3 балла |
| Применение признака перпендикулярности плоскостей | 1 балл | |||
| Оформление решения задачи | 1 балл | |||
| 2 | Расстояние между скрещивающимися прямыми | Определение расстояние между скрещивающимися прямыми | 1 балл | 3 балла |
| Оформление решения задачи | 2 балла | |||
| 3 | Перпендикулярные плоскости | Знание и применение свойств перпендикулярных плоскостей | 2 балла | 5 баллов |
| Выполнение построения | 1 балл | |||
| Оформление решения задачи | 2 балла | |||
| 4 | Свойства параллельных плоскостей | Выполнение чертежа по условию задачи | 1 балл | 5 баллов |
| Применение свойств параллельных плоскостей | 1 балл | |||
| Составление уравнения | 1 балл | |||
| Оформление решения задачи | 2 балла | |||
| 5 | Угол между прямой и плоскостью | Выполнение чертежа по условию задачи | 2 балла | 5 баллов |
| Нахождение углов | 2 балла | |||
| Оформление решения задачи | 1 балл |
Критерии оценивания:
1-10 баллов – «2»
11-15 баллов – «3»
16-19 баллов – «4»
20-21 балл – «5»
Контрольная работа №6 10 класс.
Тема: «Координаты и векторы в пространстве».
Цель: проверить уровень усвоения ГОСО:
- знания и умения применять при решении задач формул нахождения середины отрезка, расстояние между точками
- знания и умения применять при решении задач нахождение координат и модуля вектора, условия перпендикулярности и коллинеарности векторов, скалярное произведение векторов;
- умение оформлять решение задачи.
| I вариант. |
| 1.Найдите координаты точек, симметричных точке А ( 7 ; -3 ; 1 ): а) плоскости XZ, б) оси Y, в) начала координат. 2.Дан треугольник АВС с вершинами А (11; -2;- 9) , В(2;6;-4), С (8;-6;-8) а) найдите координаты середины отрезка ВС, б) найдите координаты и модуль вектора ВС, в) найдите вектор АВ + BC, г) докажите перпендикулярность векторов AB и AC. 3. Дан вектор а (2; 1; -2) а) известно, что а = EF. Найдите координаты точки Е, если F (4;-1;-2) б) Найдите значения m и n, при которых векторы a и b коллинеарны, если b (-4; m; n) в) Найдите координаты и модуль вектора с, если с = 2а 4. Даны векторы a(-3; 0; 4) и b(1; -2; 2) а) Найдите вектор 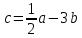 б) Найдите (a + b)(a – b) в) Найдите косинус угла между векторами a и b 5. Докажите, что четырехугольник параллелограмм, и найдите его центр симметрии, если А(-2;-4;1), В(-5;-6;-1), С(4;10;3), Р(7;12;5). |
| II вариант. |
| 1. Найдите координаты точек, симметричных точке: В (2 ; 4 ; -5): а) плоскости XY, б) оси Х, в) начала координат 2. Дан треугольник АВС с вершинами А (11; -2; - 9) , В(2;6;-4), С (14; 2; -10) а) найдите координаты середины отрезка ВС, б) найдите координаты и модуль вектора ВС, в) найдите вектор АВ + BC; г) докажите перпендикулярность векторов AB и AC 3. Дан вектор а (2; 1; -2) а) известно, что а = EF. Найдите координаты точки F, если E (2;0;3) б) Найдите значения m и n, при которых векторы a и b коллинеарны, если b (m; n; -4) в) Найдите координаты и модуль вектора с, если с = -3а 4. Даны векторы a(-2; -2; 1) и b(0; -4; 3) а) Найдите вектор 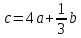 б) Найдите (a + b) (a – b) в) Найдите косинус угла между векторами a и b 5.Докажите, что четырехугольник параллелограмм, и найдите его центр симметрии, если А(-1;4;3), В(-3;6;-5), С(3;0;-5), Р(5;-2;3) |
Распределение заданий по содержанию и уровню сложности
| Содержательная линия | Воспроиз-ведение знаний | Примене-ние знаний | Интеграция знаний | Процентное соотношение в тексте |
| Преобразование симметрии | №1 | | | 20 % |
| Координаты в пространстве | №2 | | | 20 % |
| Векторы в пространстве | | №3, №4 | №5 | 60% |
| Процентное соотношение заданий | 40 % | 40 % | 20 % | 100 % |
Спецификация заданий и критерии оценивания
| № задания | Характеристика задания | Проверяемые элементы | Балл за выполнение проверяемо-го элемента | Балл за вы-полнение задания |
| 1 | Координаты в пространстве. | Координаты точек симметричных относительно координатной плоскости | 1 балл | 3 балла |
| Координаты точек симметричных относительно координатной оси | 1 балл | |||
| Координаты точек симметричных относительно начала координат | 1 балл | |||
| 2 | Координаты и векторы. | Координаты середины отрезка | 1 балл | 5 баллов |
| Координаты и модуль вектора | 1 балл | |||
| Координаты суммы векторов | 1 балл | |||
| Условие перпендикулярности векторов | 1 балл | |||
| Оформление решения задачи | 1 балл | |||
| 3 | Координаты и векторы. | Координаты начала вектора | 1 балл | 5 баллов |
| Условие коллинеарности | 1 балл | |||
| Координаты вектора | 1 балл | |||
| Модуль вектора | 1 балл | |||
| Оформление решения задачи | 1 балл | |||
| 4 | Координаты и векторы. | Координаты вектора | 1 балл | 5 баллов |
| Скалярное произведение векторов | 1 балл | |||
| Нахождение косинуса | 2 балла | |||
| Оформление решения задачи | 1 балл | |||
| 5 | Координаты и векторы. | Применение признаков параллелограмма | 2 балла | 5 баллов |
| Нахождение центра симметрии | 2 балла | |||
| Оформление решения задачи | 1 балл |