Файл: Курсовая работа Гидравлический расчет сложного трубопровода и элементов оборудования.docx
Добавлен: 11.01.2024
Просмотров: 141
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
=  = 0,042.
= 0,042.
По формуле Дарси – Вейсбаха вычислим значения суммарных потерь напора во втором трубопроводе. Так как во втором трубопроводе нет местных сопротивлений, то при вычислении h, коэффициент берем равным нулю:
h, коэффициент берем равным нулю:
 h =
h = 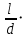
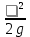 = 0,042
= 0,042  4,24 м.
4,24 м.
Найдем величины статического напора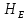 для последующего построения гидравлической характеристики трубопровода:
для последующего построения гидравлической характеристики трубопровода:
 = 2 +
= 2 + 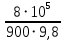 – 4,24 = 88,366 м.
– 4,24 = 88,366 м.
Результаты расчета сведем в таблицу 1.
Таблица 1 – Гидравлический расчет 2-го трубопровода
2.2. Гидравлический расчет 3-го трубопровода:
Расчет трубопровода для = 1 м/с:
Q2 = 3S = 1 ⋅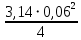 = 0,00283
= 0,00283  .
.
По найденным значениям расхода найдем значения числа Рейнольдса:
Re = =
= 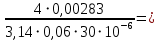 2002,83.
2002,83.
Анализируя полученные данные, (Re< Reкр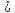 вычисляем коэффициент Дарси по формуле Стокса:
вычисляем коэффициент Дарси по формуле Стокса:
= =
= 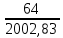 = 0,032
= 0,032
По формуле Дарси – Вейсбаха вычислим значения суммарных потерь напора в третьем трубопроводе. Так как в третьем трубопроводе нет местных сопротивлений, то при вычислении h, коэффициент берем равным нулю:
h, коэффициент берем равным нулю:
 h =
h = 
 = 0,032
= 0,032  4,08 м.
4,08 м.
Найдем величины статического напора для последующего построения гидравлической характеристики трубопровода:
для последующего построения гидравлической характеристики трубопровода:
 = 6 +
= 6 +  + 4,08 = 21,408 м.
+ 4,08 = 21,408 м.
Таблица 2 – Гидравлический расчет 3-го трубопровода

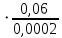 = 3000,
= 3000,
 = 150000.
= 150000.
2.3. Гидравлический расчет 4-го трубопровода:
Расчет трубопровода для = 1 м/с:
Q2 = 4S = 1 ⋅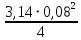 = 0,00502
= 0,00502  .
.
По найденным значениям расхода найдем значения числа Рейнольдса:
Re = =
= 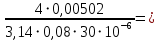 2664,67.
2664,67.
Граничные числа Рейнольдса:

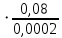 = 4000,
= 4000,
 = 200000.
= 200000.
Анализируя полученные данные, (Reкр1  вычисляем коэффициент Дарси по формуле Блазиуса:
вычисляем коэффициент Дарси по формуле Блазиуса:
= =
=  = 0,044.
= 0,044.
По формуле Дарси – Вейсбаха вычислим значения суммарных потерь напора в четвертом трубопроводе. Так как в четвёртом трубопроводе есть местные сопротивления, то при вычислении h, коэффициент берем равным 0,15:
h, коэффициент берем равным 0,15:
 h = (
h = (
 = (0,044
= (0,044  3,65 м.
3,65 м.
Найдем величины статического напора для последующего построения гидравлической характеристики трубопровода:
для последующего построения гидравлической характеристики трубопровода:
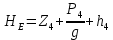 = 6 +
= 6 +  + 3,65 = 20,973 м.
+ 3,65 = 20,973 м.
Таблица 3 – Гидравлический расчет 4-го трубопровода
На основании вычисленных данных строим график уравнений (2), (3), (4), (5) в координатах H – Q.

A
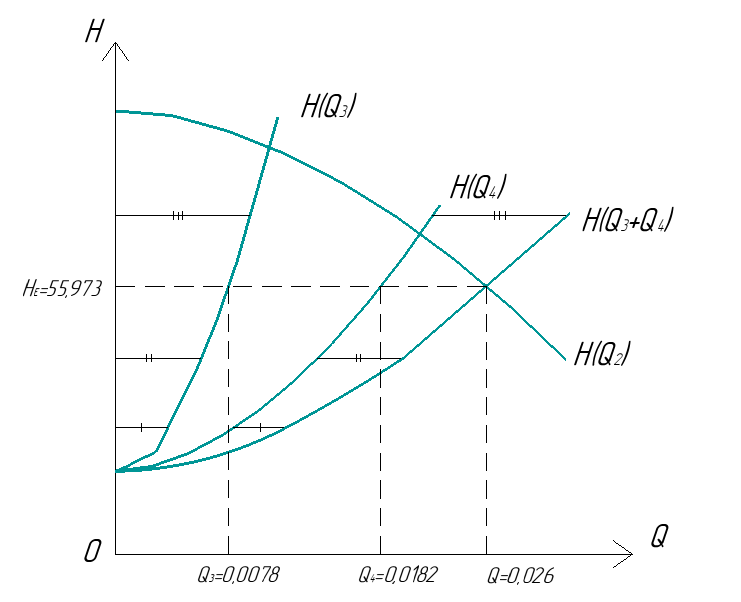
График 1
Построенные кривые на графике 1 являются графическим изображением уравнений (2), (3), (4). На основании уравнения (5), сложив графически кривые H(Q3) и H(Q4) путем добавления расхода в трубопроводе 3 к расходу в трубопроводе 4 при одинаковом значении напора, получаем кривую, представляющую собой эквивалентную гидравлическую характеристику трубопроводов 3 и 4, т.е. H(Q3 + Q4).
Точка А пересечения кривых H(Q2) и H(Q3 + Q4) дает графическое решение относительно напора в узле E и расхода Q.
Так как кривая H(Q3 + Q4) получена путем сложения расходов в трубопроводах 3 и 4, то, проведя горизонтальную прямую от точки А до пересечения с кривыми H(Q3) и H(Q4), получим значения расходов Q3 и Q4.
Q = Q2 = 0,026 = 93,6
= 93,6  ,
,
Q3 = 0,0078 = 28,08
= 28,08  ,
,
Q4 = 0,0182 = 65,52
= 65,52  .
.
Приведенные расчеты показали, что проектный расход в трубопроводе составляет Q = 93,6 .
.
Для нахождения Pвх составим уравнение Бернулли для участка трубопровода l1d1:
Z1 + = Zвх +
= Zвх +  +
+  .
.
Расход на участке l1d1 трубопровода равен расходу на участке l2d2. Отсюда можем найти скорость потока 1:
1 =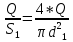 ,
,
где S1 – площадь сечения трубопровода 1.
Подставляя численные значения получим:
1 =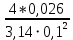 = 3,312
= 3,312 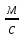 .
.
Определим число Рейнольдса:
Re = =
=  = 11040.
= 11040.
Вычислим граничные значения ReI и ReII:

 = 5000,
= 5000,
 = 250000.
= 250000.
Сравнивая вычисленное число Re с граничными и критическим ReI < Re < ReII делаем вывод, что режим движения турбулентный, зона гидравлических гладких труб, и определяем по формуле Альтшуля:
= =0,033
=0,033
Находим суммарные потери напора на участке l1d1, с учетом местного сопротивления в виде плавного колена (90), коэффициент которого 1 = 0,23, и прижимной коробки трубы с клапаном и сеткой, с коэффициентом 2 = 7 [2]:
h1 = (1 + 2 + 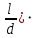
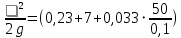
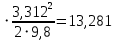 м.
м.
Выразим Pвх из уравнения Бернулли для первого трубопровода:
Pвх = g(Z1 – Zвх +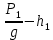 ),
),
Подставляя численные значения получим:
Pвх = 900 9,8 (0 – 2
9,8 (0 – 2  ) = – 33453,42 Па.
) = – 33453,42 Па.
3. Расчет расходов Q, Q2, Q3, Q4 при изменении вязкости жидкости в 0.6 раз.
Проверим зависимость расходов от вязкости, построив гидравлические характеристики труб, по которым течет жидкость с вязкостью в 0,6????. Новая вязкость примет значение ???? = 18*10-6 м2/c. Будем считать, что давление на выходе из насоса осталось прежним.
Решение:
3.1. Гидравлический расчет 2-го трубопровода:
Расчет трубопровода для = 1 м/с:
Q2 = 4S = 1 ⋅ = 0,00785
= 0,00785  .
.
По найденным значениям расхода найдем значения числа Рейнольдса:
Re = =
= 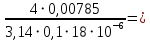 5555,56.
5555,56.
Граничные числа Рейнольдса:

 = 5000,
= 5000,
 = 250000.
= 250000.
Анализируя полученные данные, (ReI1I  вычисляем коэффициент Дарси по формуле Альштуля:
вычисляем коэффициент Дарси по формуле Альштуля:
= =0,038
=0,038
По формуле Дарси – Вейсбаха вычислим значения суммарных потерь напора во втором трубопроводе. Так как во втором трубопроводе нет местных сопротивлений, то при вычислении h, коэффициент берем равным 0:
h, коэффициент берем равным 0:
 h =
h = 
 = 0,038
= 0,038 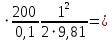 3,87 м.
3,87 м.
Найдем величины статического напора для последующего построения гидравлической характеристики трубопровода:
для последующего построения гидравлической характеристики трубопровода:
 = 2 +
= 2 + 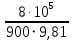 - 3,87 = 88,737 м.
- 3,87 = 88,737 м.
Таблица 4 – Гидравлический расчет 2-го трубопровода
3.2. Гидравлический расчет 3-го трубопровода:
Расчет трубопровода для = 1 м/с:
Q2 = 4S = 1 ⋅ = 0,002826
= 0,002826  .
.
По найденным значениям расхода найдем значения числа Рейнольдса:
Re = =
= 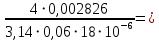 3333,33.
3333,33.
Граничные числам Рейнольдса:

 = 3000,
= 3000,
 = 150000.
= 150000.
Анализируя полученные данные, (ReI1I  вычисляем коэффициент Дарси по формуле Альштуля:
вычисляем коэффициент Дарси по формуле Альштуля:
=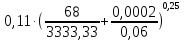 =0,043
=0,043
По формуле Дарси – Вейсбаха вычислим значения суммарных потерь напора в третьем трубопроводе. Так как в третьем трубопроводе нет местных сопротивлений, то при вычислении h, коэффициент берем равным 0:
h, коэффициент берем равным 0:
 h =
h = 
 = 0,043
= 0,043  5,50 м.
5,50 м.
Найдем величины статического напора для последующего построения гидравлической характеристики трубопровода:
для последующего построения гидравлической характеристики трубопровода:
 = 6 +
= 6 +  + 5,50 = 22,828 м.
+ 5,50 = 22,828 м.
Таблица 5 – Гидравлический расчет 3-го трубопровода
3.3. Гидравлический расчет 4-го трубопровода:
Расчет трубопровода для = 1 м/с:
Q2 = 4S = 1 ⋅ = 0,005024
= 0,005024  .
.
По найденным значениям расхода найдем значения числа Рейнольдса:
Re = =
=  4444,44.
4444,44.
Граничные числам Рейнольдса:

 = 4000,
= 4000,
 = 200000.
= 200000.
Анализируя полученные данные, (ReII1  вычисляем коэффициент Дарси по формуле Альштуля:
вычисляем коэффициент Дарси по формуле Альштуля:
=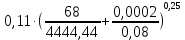 =0,040
=0,040
По формуле Дарси – Вейсбаха вычислим значения суммарных потерь напора в четвертом трубопроводе. Так как в четвёртом трубопроводе есть местные сопротивления, то при вычислении h, коэффициент берем равным 0,15:
h, коэффициент берем равным 0,15:
 h =(0,15+
h =(0,15+ 
 =(0,15+ 0,040
=(0,15+ 0,040 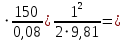 3,33 м.
3,33 м.
Найдем величины статического напора для последующего построения гидравлической характеристики трубопровода:
для последующего построения гидравлической характеристики трубопровода:
 = 6 +
= 6 +  + 3,33 = 20,654 м.
+ 3,33 = 20,654 м.
Таблица 6 – Гидравлический расчет 4-го трубопровода
На основании вычисленных данных строим график уравнений (2), (3), (4), (5) в координатах H – Q.






График 2
Так как кривая HE (Q3 + Q4) на графике 2 получена путем сложения расходов в трубопроводах 3 и 4, то, проведя горизонтальную прямую от точки А до пересечения с кривыми (3) и (4), получим значения расходов Q3 и Q4.
Q = Q2 = 0,0274 = 98,64
= 98,64  ,
,
Q3 = 0,0082 = 29,52
= 29,52  ,
,
Q4 = 0,0192 = 69,12
= 69,12  .
.
Приведенные расчеты показали, что проектный расход трубопровода составляет Q = 98,64 . Сравнивая проектный расход при вязкости жидкости ν и при 0,6ν, можно сделать вывод, что при уменьшении вязкости перекачиваемой жидкости при прочих равных условиях расход в трубопроводе увеличивается.
. Сравнивая проектный расход при вязкости жидкости ν и при 0,6ν, можно сделать вывод, что при уменьшении вязкости перекачиваемой жидкости при прочих равных условиях расход в трубопроводе увеличивается.
В результате выполнения курсовой работы мной была освоена компетенция ОПК-1: Способность решать задачи, относящиеся к профессиональной деятельности, применяя методы моделирования, математического анализа, естественнонаучные и общеинженерные знания.
В ходе выполнения курсового проекта был произведен расчет разветвленного трубопровода, а именно:
1.Гидравлика, гидромашины и гидроприводы: учеб.для втузов / Т. М. Башта, Б. Б. Некрасов, С. С. Руднев. - 2-е изд., перераб. - М. : Машиностроение, 1982. - 423 с. : ил. - Библиогр.: с.418.
2. Сборник задач по гидравлике и газодинамике для нефтегазовых вузов / И. М. Астрахан, В. Г. Иванников, В. В. Кадет, И. Н. Кочина; РГУ нефти и газа им. И.М. Губкина. - М. : Грифон, 2007. - 304 с.
3.Сборник задач по машиностроительной гидравлике: учеб. пособие для вузов / ред. И. И. Куколевский, ред. Л. Г. Подвидз. - 5-е изд., стереотип. - М. : Изд-во МГТУ им. Н.Э. Баумана, 2002. - 448 с.
 = 0,042.
= 0,042.По формуле Дарси – Вейсбаха вычислим значения суммарных потерь напора во втором трубопроводе. Так как во втором трубопроводе нет местных сопротивлений, то при вычислении
 h, коэффициент берем равным нулю:
h, коэффициент берем равным нулю: h =
h = 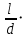
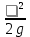 = 0,042
= 0,042  4,24 м.
4,24 м.Найдем величины статического напора
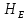 для последующего построения гидравлической характеристики трубопровода:
для последующего построения гидравлической характеристики трубопровода: = 2 +
= 2 + 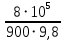 – 4,24 = 88,366 м.
– 4,24 = 88,366 м.Результаты расчета сведем в таблицу 1.
Таблица 1 – Гидравлический расчет 2-го трубопровода
| № | Скорость, υ м/с | Расход, Q  /с /с | Расход, Q  /ч /ч | Число Рейнольдса Re | Коэффициент Дарси | Потери  h, м h, м | гидростатический напор H(Q2), м |
| 0 | 0 | 0 | 0 | 0,00 | 0,000 | 0,00 | 92,610 |
| 1 | 0,5 | 0,003925 | 14,13 | 1 666,67 | 0,038 | 0,97 | 91,642 |
| 2 | 1 | 0,00785 | 28,26 | 3 333,33 | 0,042 | 4,24 | 88,366 |
| 3 | 1,5 | 0,011775 | 42,39 | 5 000,00 | 0,039 | 8,92 | 83,694 |
| 4 | 2 | 0,0157 | 56,52 | 6 666,67 | 0,037 | 14,91 | 77,704 |
| 5 | 2,5 | 0,019625 | 70,65 | 8 333,33 | 0,035 | 22,25 | 70,361 |
| 6 | 3 | 0,02355 | 84,78 | 10 000,00 | 0,034 | 30,91 | 61,701 |
| 7 | 3,5 | 0,027475 | 98,91 | 11 666,67 | 0,033 | 40,86 | 51,752 |
| 8 | 4 | 0,0314 | 113,04 | 13 333,33 | 0,032 | 52,08 | 40,532 |
2.2. Гидравлический расчет 3-го трубопровода:
Расчет трубопровода для = 1 м/с:
Q2 = 3S = 1 ⋅
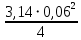 = 0,00283
= 0,00283  .
.По найденным значениям расхода найдем значения числа Рейнольдса:
Re =
 =
= 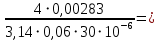 2002,83.
2002,83.Анализируя полученные данные, (Re< Reкр
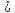 вычисляем коэффициент Дарси по формуле Стокса:
вычисляем коэффициент Дарси по формуле Стокса: =
 =
= 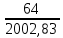 = 0,032
= 0,032По формуле Дарси – Вейсбаха вычислим значения суммарных потерь напора в третьем трубопроводе. Так как в третьем трубопроводе нет местных сопротивлений, то при вычислении
 h, коэффициент берем равным нулю:
h, коэффициент берем равным нулю: h =
h = 
 = 0,032
= 0,032  4,08 м.
4,08 м.Найдем величины статического напора
 для последующего построения гидравлической характеристики трубопровода:
для последующего построения гидравлической характеристики трубопровода: = 6 +
= 6 +  + 4,08 = 21,408 м.
+ 4,08 = 21,408 м.Таблица 2 – Гидравлический расчет 3-го трубопровода
| № | Скорость, υ м/с | Расход, Q  /с /с | Расход, Q  /ч /ч | Число Рейнольдса Re | Коэффициент Дарси | Потери  h, м h, м | гидростатический напор H(Q3), м |
| 0 | 0 | 0 | 0 | 0,00 | 0,000 | 0,00 | 17,326 |
| 1 | 0,5 | 0,001413 | 5,0868 | 1 000,00 | 0,064 | 2,04 | 19,365 |
| 2 | 1 | 0,002826 | 10,1736 | 2 002,83 | 0,032 | 4,08 | 21,408 |
| 3 | 1,5 | 0,004239 | 15,2604 | 3 000,00 | 0,044 | 12,66 | 29,990 |
| 4 | 2 | 0,005652 | 20,3472 | 4 000,00 | 0,042 | 21,17 | 38,498 |
| 5 | 2,5 | 0,007065 | 25,434 | 5 000,00 | 0,040 | 31,60 | 48,927 |
| 6 | 3 | 0,008478 | 30,5208 | 6 000,00 | 0,038 | 43,90 | 61,226 |
| 7 | 3,5 | 0,009891 | 35,6076 | 7 000,00 | 0,037 | 58,03 | 75,356 |
| 8 | 4 | 0,011304 | 40,6944 | 8 000,00 | 0,036 | 73,97 | 91,292 |

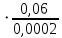 = 3000,
= 3000, = 150000.
= 150000.2.3. Гидравлический расчет 4-го трубопровода:
Расчет трубопровода для = 1 м/с:
Q2 = 4S = 1 ⋅
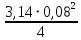 = 0,00502
= 0,00502  .
.По найденным значениям расхода найдем значения числа Рейнольдса:
Re =
 =
= 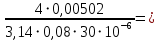 2664,67.
2664,67.Граничные числа Рейнольдса:

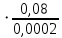 = 4000,
= 4000, = 200000.
= 200000.Анализируя полученные данные, (Reкр
 вычисляем коэффициент Дарси по формуле Блазиуса:
вычисляем коэффициент Дарси по формуле Блазиуса: =
 =
=  = 0,044.
= 0,044.По формуле Дарси – Вейсбаха вычислим значения суммарных потерь напора в четвертом трубопроводе. Так как в четвёртом трубопроводе есть местные сопротивления, то при вычислении
 h, коэффициент берем равным 0,15:
h, коэффициент берем равным 0,15: h = (
h = (
 = (0,044
= (0,044  3,65 м.
3,65 м.Найдем величины статического напора
 для последующего построения гидравлической характеристики трубопровода:
для последующего построения гидравлической характеристики трубопровода: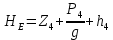 = 6 +
= 6 +  + 3,65 = 20,973 м.
+ 3,65 = 20,973 м.Таблица 3 – Гидравлический расчет 4-го трубопровода
| № | Скорость, υ м/с | Расход, Q  /с /с | Расход, Q  /ч /ч | Число Рейнольдса Re | Коэффиц иент Дарси | Потери  h, м h, м | гидростатический напор H(Q4), м |
| 0 | 0 | 0 | 0 | 0,00 | 0,000 | 0,00 | 17,326 |
| 1 | 0,5 | 0,002512 | 9,0432 | 1 333,33 | 0,048 | 1,00 | 18,322 |
| 2 | 1 | 0,005024 | 18,0864 | 2 666,67 | 0,044 | 3,65 | 20,981 |
| 3 | 1,5 | 0,007536 | 27,1296 | 4 000,00 | 0,041 | 7,68 | 25,004 |
| 4 | 2 | 0,010048 | 36,1728 | 5 333,33 | 0,039 | 12,84 | 30,163 |
| 5 | 2,5 | 0,01256 | 45,216 | 6 666,67 | 0,037 | 19,16 | 36,489 |
| 6 | 3 | 0,015072 | 54,2592 | 8 000,00 | 0,036 | 26,62 | 43,950 |
| 7 | 3,5 | 0,017584 | 63,3024 | 9 333,33 | 0,035 | 35,20 | 52,522 |
| 8 | 4 | 0,020096 | 72,3456 | 10 666,67 | 0,034 | 44,86 | 62,190 |
На основании вычисленных данных строим график уравнений (2), (3), (4), (5) в координатах H – Q.

A

График 1
Построенные кривые на графике 1 являются графическим изображением уравнений (2), (3), (4). На основании уравнения (5), сложив графически кривые H(Q3) и H(Q4) путем добавления расхода в трубопроводе 3 к расходу в трубопроводе 4 при одинаковом значении напора, получаем кривую, представляющую собой эквивалентную гидравлическую характеристику трубопроводов 3 и 4, т.е. H(Q3 + Q4).
Точка А пересечения кривых H(Q2) и H(Q3 + Q4) дает графическое решение относительно напора в узле E и расхода Q.
Так как кривая H(Q3 + Q4) получена путем сложения расходов в трубопроводах 3 и 4, то, проведя горизонтальную прямую от точки А до пересечения с кривыми H(Q3) и H(Q4), получим значения расходов Q3 и Q4.
Q = Q2 = 0,026
 = 93,6
= 93,6  ,
,Q3 = 0,0078
 = 28,08
= 28,08  ,
,Q4 = 0,0182
 = 65,52
= 65,52  .
.Приведенные расчеты показали, что проектный расход в трубопроводе составляет Q = 93,6
 .
.Для нахождения Pвх составим уравнение Бернулли для участка трубопровода l1d1:
Z1 +
 = Zвх +
= Zвх +  +
+  .
.Расход на участке l1d1 трубопровода равен расходу на участке l2d2. Отсюда можем найти скорость потока 1:
1 =
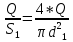 ,
,где S1 – площадь сечения трубопровода 1.
Подставляя численные значения получим:
1 =
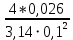 = 3,312
= 3,312 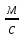 .
.Определим число Рейнольдса:
Re =
 =
=  = 11040.
= 11040.Вычислим граничные значения ReI и ReII:

 = 5000,
= 5000, = 250000.
= 250000.Сравнивая вычисленное число Re с граничными и критическим ReI < Re < ReII делаем вывод, что режим движения турбулентный, зона гидравлических гладких труб, и определяем по формуле Альтшуля:
=
 =0,033
=0,033Находим суммарные потери напора на участке l1d1, с учетом местного сопротивления в виде плавного колена (90), коэффициент которого 1 = 0,23, и прижимной коробки трубы с клапаном и сеткой, с коэффициентом 2 = 7 [2]:
h1 = (1 + 2 +
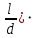
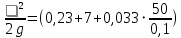
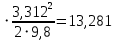 м.
м.Выразим Pвх из уравнения Бернулли для первого трубопровода:
Pвх = g(Z1 – Zвх +
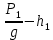 ),
),Подставляя численные значения получим:
Pвх = 900
 9,8 (0 – 2
9,8 (0 – 2  ) = – 33453,42 Па.
) = – 33453,42 Па.
1 2 3
3. Расчет расходов Q, Q2, Q3, Q4 при изменении вязкости жидкости в 0.6 раз.
Проверим зависимость расходов от вязкости, построив гидравлические характеристики труб, по которым течет жидкость с вязкостью в 0,6????. Новая вязкость примет значение ???? = 18*10-6 м2/c. Будем считать, что давление на выходе из насоса осталось прежним.
Решение:
3.1. Гидравлический расчет 2-го трубопровода:
Расчет трубопровода для = 1 м/с:
Q2 = 4S = 1 ⋅
 = 0,00785
= 0,00785  .
.По найденным значениям расхода найдем значения числа Рейнольдса:
Re =
 =
= 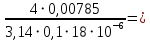 5555,56.
5555,56.Граничные числа Рейнольдса:

 = 5000,
= 5000, = 250000.
= 250000.Анализируя полученные данные, (ReI
 вычисляем коэффициент Дарси по формуле Альштуля:
вычисляем коэффициент Дарси по формуле Альштуля: =
 =0,038
=0,038По формуле Дарси – Вейсбаха вычислим значения суммарных потерь напора во втором трубопроводе. Так как во втором трубопроводе нет местных сопротивлений, то при вычислении
 h, коэффициент берем равным 0:
h, коэффициент берем равным 0: h =
h = 
 = 0,038
= 0,038 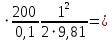 3,87 м.
3,87 м.Найдем величины статического напора
 для последующего построения гидравлической характеристики трубопровода:
для последующего построения гидравлической характеристики трубопровода: = 2 +
= 2 + 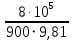 - 3,87 = 88,737 м.
- 3,87 = 88,737 м.Таблица 4 – Гидравлический расчет 2-го трубопровода
| № | Скорость, υ м/с | Расход, Q  /с /с | Расход, Q  /ч /ч | Число Рейнольдса Re | Коэффиц иент Дарси | Потери  h, м h, м | Гидростат ический напор H(Q2), м |
| 0 | 0 | 0 | 0 | 0,00 | 0,000 | 0,00 | 92,610 |
| 1 | 0,5 | 0,003925 | 14,13 | 2 777,78 | 0,044 | 1,11 | 91,500 |
| 2 | 1 | 0,00785 | 28,26 | 5 555,56 | 0,038 | 3,87 | 88,737 |
| 3 | 1,5 | 0,011775 | 42,39 | 8 333,33 | 0,035 | 8,01 | 84,601 |
| 4 | 2 | 0,0157 | 56,52 | 11 111,11 | 0,033 | 13,46 | 79,147 |
| 5 | 2,5 | 0,019625 | 70,65 | 13 888,89 | 0,032 | 20,19 | 72,415 |
| 6 | 3 | 0,02355 | 84,78 | 16 666,67 | 0,031 | 28,18 | 64,430 |
| 7 | 3,5 | 0,027475 | 98,91 | 19 444,44 | 0,030 | 37,40 | 55,209 |
| 8 | 4 | 0,0314 | 113,04 | 22 222,22 | 0,029 | 47,85 | 44,761 |
3.2. Гидравлический расчет 3-го трубопровода:
Расчет трубопровода для = 1 м/с:
Q2 = 4S = 1 ⋅
 = 0,002826
= 0,002826  .
.По найденным значениям расхода найдем значения числа Рейнольдса:
Re =
 =
= 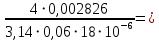 3333,33.
3333,33.Граничные числам Рейнольдса:

 = 3000,
= 3000, = 150000.
= 150000.Анализируя полученные данные, (ReI
 вычисляем коэффициент Дарси по формуле Альштуля:
вычисляем коэффициент Дарси по формуле Альштуля: =
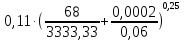 =0,043
=0,043По формуле Дарси – Вейсбаха вычислим значения суммарных потерь напора в третьем трубопроводе. Так как в третьем трубопроводе нет местных сопротивлений, то при вычислении
 h, коэффициент берем равным 0:
h, коэффициент берем равным 0: h =
h = 
 = 0,043
= 0,043  5,50 м.
5,50 м.Найдем величины статического напора
 для последующего построения гидравлической характеристики трубопровода:
для последующего построения гидравлической характеристики трубопровода: = 6 +
= 6 +  + 5,50 = 22,828 м.
+ 5,50 = 22,828 м.Таблица 5 – Гидравлический расчет 3-го трубопровода
| № | Скоро сть, υ м/с | Расход, Q  /с /с | Расход, Q  /ч /ч | Число Рейнольдса Re | Коэффициент Дарси | Потери  h, м h, м | гидростати ческий напор H(Q3), м |
| 0 | 0 | 0 | 0 | 0,00 | 0,000 | 0,00 | 17,326 |
| 1 | 0,5 | 0,001413 | 5,0868 | 1 666,67 | 0,038 | 1,21 | 18,536 |
| 2 | 1 | 0,002826 | 10,1736 | 3 333,33 | 0,043 | 5,50 | 22,828 |
| 3 | 1,5 | 0,004239 | 15,2604 | 5 000,00 | 0,040 | 11,38 | 28,703 |
| 4 | 2 | 0,005652 | 20,3472 | 6 666,67 | 0,038 | 19,12 | 36,449 |
| 5 | 2,5 | 0,007065 | 25,434 | 8 333,33 | 0,036 | 28,68 | 46,009 |
| 6 | 3 | 0,008478 | 30,5208 | 10 000,00 | 0,035 | 40,02 | 57,350 |
| 7 | 3,5 | 0,009891 | 35,6076 | 11 666,67 | 0,034 | 53,12 | 70,447 |
| 8 | 4 | 0,011304 | 40,6944 | 13 333,33 | 0,033 | 67,96 | 85,286 |
3.3. Гидравлический расчет 4-го трубопровода:
Расчет трубопровода для = 1 м/с:
Q2 = 4S = 1 ⋅
 = 0,005024
= 0,005024  .
.По найденным значениям расхода найдем значения числа Рейнольдса:
Re =
 =
=  4444,44.
4444,44.Граничные числам Рейнольдса:

 = 4000,
= 4000, = 200000.
= 200000.Анализируя полученные данные, (ReI
 вычисляем коэффициент Дарси по формуле Альштуля:
вычисляем коэффициент Дарси по формуле Альштуля: =
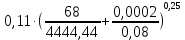 =0,040
=0,040По формуле Дарси – Вейсбаха вычислим значения суммарных потерь напора в четвертом трубопроводе. Так как в четвёртом трубопроводе есть местные сопротивления, то при вычислении
 h, коэффициент берем равным 0,15:
h, коэффициент берем равным 0,15: h =(0,15+
h =(0,15+ 
 =(0,15+ 0,040
=(0,15+ 0,040 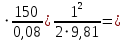 3,33 м.
3,33 м.Найдем величины статического напора
 для последующего построения гидравлической характеристики трубопровода:
для последующего построения гидравлической характеристики трубопровода: = 6 +
= 6 +  + 3,33 = 20,654 м.
+ 3,33 = 20,654 м.Таблица 6 – Гидравлический расчет 4-го трубопровода
| № | Скорость, υ м/с | Расход, Q  /с /с | Расход, Q  /ч /ч | Число Рейнольдса Re | Коэффициент Дарси | Потери  h, м h, м | гидростати ческий напор H(Q4), м |
| 0 | 0 | 0 | 0 | 0,00 | 0,000 | 0,00 | 17,326 |
| 1 | 0,5 | 0,002512 | 9,0432 | 2 222,22 | 0,046 | 0,95 | 18,280 |
| 2 | 1 | 0,005024 | 18,0864 | 4 444,44 | 0,040 | 3,33 | 20,654 |
| 3 | 1,5 | 0,007536 | 27,1296 | 6 666,67 | 0,037 | 6,88 | 24,208 |
| 4 | 2 | 0,010048 | 36,1728 | 8 888,89 | 0,035 | 11,57 | 28,893 |
| 5 | 2,5 | 0,01256 | 45,216 | 11 111,11 | 0,034 | 17,35 | 34,676 |
| 6 | 3 | 0,015072 | 54,2592 | 13 333,33 | 0,032 | 24,21 | 41,536 |
| 7 | 3,5 | 0,017584 | 63,3024 | 15 555,56 | 0,032 | 32,13 | 49,459 |
| 8 | 4 | 0,020096 | 72,3456 | 17 777,78 | 0,031 | 41,11 | 58,435 |
На основании вычисленных данных строим график уравнений (2), (3), (4), (5) в координатах H – Q.






Так как кривая HE (Q3 + Q4) на графике 2 получена путем сложения расходов в трубопроводах 3 и 4, то, проведя горизонтальную прямую от точки А до пересечения с кривыми (3) и (4), получим значения расходов Q3 и Q4.
Q = Q2 = 0,0274
 = 98,64
= 98,64  ,
,Q3 = 0,0082
 = 29,52
= 29,52  ,
,Q4 = 0,0192
 = 69,12
= 69,12  .
.Приведенные расчеты показали, что проектный расход трубопровода составляет Q = 98,64
 . Сравнивая проектный расход при вязкости жидкости ν и при 0,6ν, можно сделать вывод, что при уменьшении вязкости перекачиваемой жидкости при прочих равных условиях расход в трубопроводе увеличивается.
. Сравнивая проектный расход при вязкости жидкости ν и при 0,6ν, можно сделать вывод, что при уменьшении вязкости перекачиваемой жидкости при прочих равных условиях расход в трубопроводе увеличивается.Заключение
В результате выполнения курсовой работы мной была освоена компетенция ОПК-1: Способность решать задачи, относящиеся к профессиональной деятельности, применяя методы моделирования, математического анализа, естественнонаучные и общеинженерные знания.
В ходе выполнения курсового проекта был произведен расчет разветвленного трубопровода, а именно:
-
Определены расходы трубопроводов Q, Q3, Q4 при вязкости равной ???? = 30*10-6 м2/c; -
Определено необходимое входное давления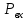 на манометре перед входом в насос при вязкости равной ???? = 30*10-6 м2/c;
на манометре перед входом в насос при вязкости равной ???? = 30*10-6 м2/c; -
Определены расходы трубопроводов Q, Q3, Q4 при вязкости равной ???? = 18*10-6 м2/c.
СПИСОК ЛИТЕРАТУРЫ
1.Гидравлика, гидромашины и гидроприводы: учеб.для втузов / Т. М. Башта, Б. Б. Некрасов, С. С. Руднев. - 2-е изд., перераб. - М. : Машиностроение, 1982. - 423 с. : ил. - Библиогр.: с.418.
2. Сборник задач по гидравлике и газодинамике для нефтегазовых вузов / И. М. Астрахан, В. Г. Иванников, В. В. Кадет, И. Н. Кочина; РГУ нефти и газа им. И.М. Губкина. - М. : Грифон, 2007. - 304 с.
3.Сборник задач по машиностроительной гидравлике: учеб. пособие для вузов / ред. И. И. Куколевский, ред. Л. Г. Подвидз. - 5-е изд., стереотип. - М. : Изд-во МГТУ им. Н.Э. Баумана, 2002. - 448 с.
1 2 3