ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 37
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
М
 ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение
высшего образования
«Тольяттинский государственный университет»
(наименование института полностью)
Кафедра /департамент /центр1 __________________________________________________
(наименование кафедры/департамента/центра полностью)
(код и наименование направления подготовки, специальности)
(направленность (профиль) / специализация)
Практическое задание №4
по учебному курсу «Эконометрика»
(наименование учебного курса)
Вариант 1
| Студент | | |
| | (И.О. Фамилия) | |
| Группа | | |
| | | |
| Преподаватель | | |
| | (И.О. Фамилия) | |
Тольятти 20__
Бланк выполнения задания 4
| № п/п | Пункт исследования | Ответ | ||||||||||||||||||||||||||||||||
| 1. | Для каждого уравнения модели определите его идентифицируемость, применив необходимое и достаточное условие идентификации. | Проверим необходимое условие идентификации для трех уравнений модели. 1. Первое уравнение включает эндогенные переменные ( 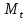 , , 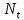 , , 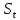 ) и две предопределенные ( ) и две предопределенные (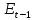 и и 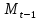 ). Тогда число предопределенных переменных, не входящих в это уравнение, плюс 1, равно числу эндогенных переменных, входящих в уравнение, а именно 2+1=3. Следовательно уравнение идентифицировано. ). Тогда число предопределенных переменных, не входящих в это уравнение, плюс 1, равно числу эндогенных переменных, входящих в уравнение, а именно 2+1=3. Следовательно уравнение идентифицировано.2. Второе уравнение включает эндогенные переменные ( 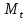 , , 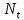 , , 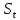 ) и одну предопределенную переменную ( ) и одну предопределенную переменную (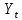 ). Тогда число предопределенных переменных, не входящих в это уравнение, плюс 1, больше числа эндогенных переменных, входящих в уравнение, а именно 3+1>3. Следовательно уравнение сверхидентифицировано. ). Тогда число предопределенных переменных, не входящих в это уравнение, плюс 1, больше числа эндогенных переменных, входящих в уравнение, а именно 3+1>3. Следовательно уравнение сверхидентифицировано.3. Третье уравнение включает эндогенные переменные ( 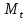 , , 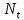 , , 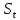 ) и одну предопределенную переменную ( ) и одну предопределенную переменную (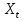 ). Тогда число предопределенных переменных, не входящих в это уравнение, плюс 1, больше числа эндогенных переменных, входящих в уравнение, а именно 3+1>3. Следовательно уравнение сверхидентифицировано. ). Тогда число предопределенных переменных, не входящих в это уравнение, плюс 1, больше числа эндогенных переменных, входящих в уравнение, а именно 3+1>3. Следовательно уравнение сверхидентифицировано.Проверим достаточное условие идентификации для трех уравнений модели. Составим матрицу коэффициентов для модели:
В соответствие с достаточным условием идентификации определитель матрицы коэффициентов, не входящих в исследуемое уравнение, не должен быть равен нулю, а ранг матрицы должен быть не менее, чем число эндогенных переменных модели минус 1, то есть в данной задаче больше или равен 3-1=2. 1. В первом уравнении матрица коэффициентов, не входящих в уравнение, имеет вид 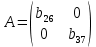 , определитель этой матрицы , определитель этой матрицы 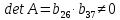 , ранг матрицы , ранг матрицы 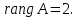 Следовательно, для первого уравнения достаточное условие выполняется, и оно точно идентифицируемо. 2. Во втором уравнении матрица коэффициентов, не входящих в уравнение, имеет вид 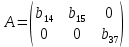 , ранг матрицы , ранг матрицы 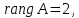 так как она содержит отличный от нуля минор второго порядка так как она содержит отличный от нуля минор второго порядка 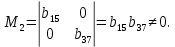 Следовательно, для второго уравнения достаточное условие выполняется, и оно сверхидентифицируемо. 2. В третьем уравнении матрица коэффициентов, не входящих в уравнение, имеет вид 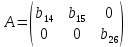 , ранг матрицы , ранг матрицы 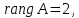 так как она содержит отличный от нуля минор второго порядка так как она содержит отличный от нуля минор второго порядка 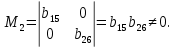 Следовательно, для второго уравнения достаточное условие выполняется, и оно сверхидентифицируемо. | ||||||||||||||||||||||||||||||||
| 2. | Определите метод оценки параметров модели. | Система является сверхидентифицируемой, для оценки параметров данной системы можно применить двухшаговый метод наименьших квадратов | ||||||||||||||||||||||||||||||||
| 3. | Запишите в общем виде приведенную форму модели. | 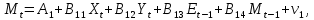 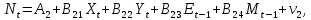 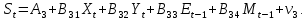 |
1 Оставить нужное