Числовые характеристики случайных величин: математическое ожидание и дисперсия
Числа, которые описывают случайные величины суммарно, называются числовыми характеристиками случайных величин.
Математическим ожиданием (МО) дискретных* случайных величин (ДСВ) называют сумму произведений всех её возможных значений на их вероятности.



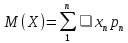
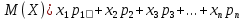
Из определения следует, что МО = const.
Найти МО(X) случайной величины можно, зная закон её распределения:

x	3	5	2
p	0,1	0,6	0,3

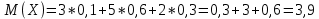
Вероятностный смысл и свойства МО
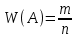- относительная частота (отличие в практике).

Математическое ожидание примерно равно среднему арифметическому наблюдаемых значений случайных величин.
Свойства:

1. 
   Математическое ожидание постоянной величины равно самой постоянной;
   

2. 
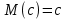
   Постоянный множитель можно выносить за знак МО;
   

3. 
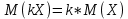
   Две случайных величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина, в противном случае, они зависимы:
   
   1. 
      Произведения независимых случайных величин X и Y определим как случайную величину X * Y, возможное значение которой равны каждому возможному значению X на каждое возможное значение Y;
      

2. 
   Сумму случайных величин X и Y определим как случайную величину X + Y, возможное значение которой равно суммам каждого возможного значения X с каждым возможным значением Y; вероятности возможных значений X+Y, равны произведениям вероятности слагаемых.
   

---

4. 
   Математическое ожидание произведения двух независимых случайных величин, равно произведению их МО:
   

Следствие: математическое ожидание произведения нескольких взаимно независимых случайных величин, равно произведению их МО.

5. 
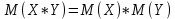
   Математическое ожидание суммы (разности) двух случайных величин равно сумме математического ожидания слагаемых:
   

Следствие: математическое ожидание нескольких случайных величин равно сумме (разности) математического ожидания слагаемых (вычитаемого).

6. 
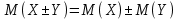
   Если все значения случайной величины X уменьшить (увеличить) на одно и то же число С, то её математическое ожидание уменьшится (увеличится) на то же число.
   

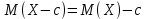
Биномиальное распределение
Математическое ожидание числа появлений события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании.


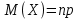
Пример задачи

Задание: издатель решил издать новую книгу. Продавать книгу он собирается за 280 руб., из которых 200 получит он сам, 50 - книжный магазин и 30 - автор. В таблице дана информация о затратах на издание книги и вероятности продажи определённого числа экземпляров книги. Найти ожидаемую прибыль издателя.

Число проданных экземпляров	Вероятность	Затраты
500	0,2	225000
1000	0,4	250000
2000	0,25	300000
3000	0,1	350000
4000	0,05	400000

Решение:

Случайная величина "прибыль" равна разности доходов от продажи и стоимости затрат. Например, если будет продано 500 экземпляров книги, то доходы от продажи равны 200*500=100000, а затраты на издание 225000 руб. Таким образом, издателю грозит убыток размером в 125000 руб. В следующей таблице обобщены ожидаемые значения случайной величины - прибыли:

---

Число	Прибыль	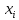Вероятность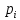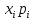
500	-125000	0,2	-25000
1000	-50000	0,4	-20000
2000	100000	0,25	25000
3000	250000	0,1	25000
4000	400000	0,05	20000
Всего		1	25000

Таким образом, получаем математическое ожидание прибыли издателя:


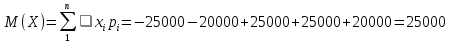
Ответ: 25000 рублей.

---------------------------------------------------------------------------------------------------------------------------

* Дискретная случайная величина — это случайная величина, множество значений которой не более чем счётно (то есть конечно или счётно).
Примечание

В большинстве случаев только математическое ожидание не может в достаточной степени характеризовать случайную величину. Случайная величина X может принимать только значения, мало отличающиеся от математического ожидания, а случайная величина Y может принимать значения, значительно отклоняющиеся от математического ожидания. Иными словами, по математическому ожиданию нельзя судить о том, какие отклонения от него, хотя бы в среднем, возможны. Для этого нужно найти дисперсию случайной величины.

Дисперсией называется математическое ожидание (то есть среднее значение) квадрата отклонения случайной величины от её среднего значения (то есть математического ожидания).

---

⇔
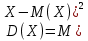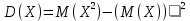
Дисперсия характеризует степень рассеяния значений случайной величины от своего среднего значения D(X).

Отклонением называется разность между случайной величиной и её математическим ожиданием

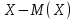
x	2	3	5
p	0,1	0,6	0,3

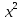	4	9	25
p	0,1	0,6	0,3

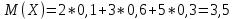
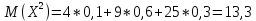
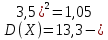
Свойства:

1. 
   Дисперсия постоянной величины C равно 0;
   

2. 
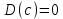
   Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат;
   

3. 
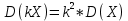
   Дисперсия суммы (разности) двух случайных величин равна сумме (разности) дисперсии этих величин;
   

4. 
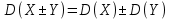
   Дисперсия случайной величины равна математическому ожиданию квадрата этой величины, из которого вычтен квадрат математического ожидания самой величины.
   

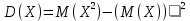
Биномиальное распределение
Дисперсия числа А в n независимых испытаниях, в каждом из которых p = const, равна произведению числа испытаний на вероятность их появления и непоявления события в одном испытании.

---

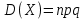
Пример задачи

Задание: в урне 6 белых и 4 чёрных шара. Из урны вынимают 3 шара. Число белых шаров среди вынутых шаров является дискретной случайной величиной X. Найти математическое ожидание и дисперсию этой случайной величины.
Решение: случайная величина X может принимать значения 0, 1, 2, 3. Соответствующие им вероятности можно вычислить по правилу умножения вероятностей. Закон распределения случайной величины:

x	0	1	2	3
p	1/30	3/10	1/2	1/6

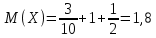
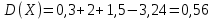
Ответ:
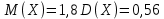
Первоисточники:

• 
  теоретический материал - http://statistica.ru/
  
• 
  практический материал - www.function-x.ru.
  

---

Смотрите также файлы

• Определение 14 марта 2023 года 35362300226 село Актогай.doc

• 08. 02. 08 Монтаж и эксплуатация оборудования и систем газоснабжения.docx

• Физической культуре.docx

• Курсовой проект По дисциплине Производственная и пожарная автоматика.docx

• Введение I. Китайское иероглифическое письмо.docx