1. 
   Выберите утверждение, являющееся аксиомой параллельных прямых
   

• 
  если прямая пересекает одну из параллельных прямых, то она пересекает и другую
  
• 
  через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной
  
• 
  если прямые параллельны третьей прямой, то они параллельны
  
• 
  если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны
  

2. 
   Прямые  с  и  Ь,  изображенные  на  чертеже, параллельны (поясните ответ).
   

3. 
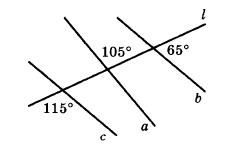
   Если прямая перпендикулярна одной из двух параллельных прямых, то
   

• 
  другую прямую она пересекает
  
• 
  другой прямой она параллельна
  
• 
  она перпендикулярна и другой
  
• 
  с другой прямой она совпадает
  

4. 
   Выберите утверждение, являющееся следствием из аксиомы параллельных прямых
   

• 
  если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую
  
• 
  если при пересечении двух прямых секущей вертикальные углы равны, то прямые параллельны
  
• 
  через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной
  
• 
  если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны
  

5. 
   Обратной теоремой к данной называется теорема, в которой
   

• 
  условие и заключение являются обратными
  
• 
  теорема доказывается методом от противного
  
• 
  условием является заключение данной теоремы, а заключением-условие данной теоремы
  
• 
  доказывается, что такого быть не может
  

6. 
   
   Если  угол  АВС  равен  30°,  а  угол  BCD  равен 160°,  то  прямые АВ  и  CD  пересекаются?
   

7. 
   Прямые а и b параллельны, с -  секущая. Один из внутренних односторонних углов равен 117  градусов. Найдите градусную меру другого внутреннего одностороннего угла. 
   

---

8. 
   ΔADB – равносторонний,  сторона  DB является медианой ΔABC. В ответе введите только числовые значения углов через пробел).                                           
   

9. 
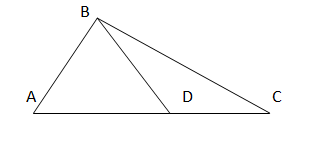
   Начертите DEFH и постройте его биссектрису FK, медиану FP и высоту FN. Найдите длину отрезка EP, если EH=4см. (В ответе запишите только числовое значение).
   

10. 
    Выберите верное утверждение вертикальных углов.
    

• 
  два угла, у которых вершины совпадают
  
• 
  три угла, стороны которых являются продолжениями сторон друг друга
  
• 
  два угла, стороны одного из которых являются продолжениями сторон другого
  
• 
  два угла, стороны которых не являются продолжениями сторон друг друга
  
• 
  любые два равных между собой угла
  

11. 
    Треугольники, изображённые на рисунке,
    

• 
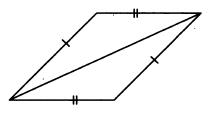
  равны по 2 сторонам и углу между ними;
  
• 
  равны по стороне и прилежащим к ней углам;
  
• 
  равны по 3 сторонам;
  
• 
  не равны.
  

12. 
    Центр вписанной окружности в любой треугольник - это
    

• 
  точка пересечения медиан
  
• 
  точка пересечения серединных перпендикуляров к сторонам треугольника
  
• 
  точка пересечения высот
  
• 
  точка пересечения биссектрис
  

13. 
    Центр описанной около любого треугольника - это
    

• 
  точка пересечения биссектрис
  
• 
  точка пересечения высот
  
• 
  точка пересечения серединных перпендикуляров к сторонам треугольника
  
• 
  точка пересечения медиан
  

14. 
    Решить задачу на построение – это значит…(расположи в правильном порядке)
    

• 
  Составить план построения фигуры
  
• 
  Реализовать план, выполнив построение
  
• 
  Доказать, что полученная фигура является искомой
  

15. 
    Определите порядок построения биссектрисы угла
    

• 
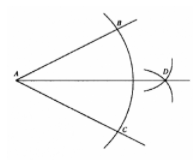
  проводим окружность произвольного радиуса с центром в вершине А данного угла
  
• 
  обозначаем как В и С точки пересечения окружности с центром в точке А со сторонами угла
  
• 
  проводим из точек В и С окружности того же радиуса, что и окружность с центром в точке А
  
• 
  обозначаем как D точку пересечения окружностей с центрами в точках В и С
  
• 
  определяем, что АD – это биссектриса угла А
  

---

16. 
    В треугольнике МКЕ угол М равен 41°, угол К на 52° больше. Вычислите угол Е.
    

17. 
    Углы треугольника АВС относятся как 5:3:1. Вычислите самый большой угол этого треугольника.
    

18. 
    Найдите самый маленький угол в треугольнике АВС, если АВ< АС<ВС.
    

 

19. 
    Один из смежных углов на 48° больше другого. Найдите меньший угол.
    

20. 
    Окружность, вписанная в равнобедренный треугольник касается его боковой стороны и делит ее на отрезки 7 и 2, считая от вершины. Найдите периметр треугольника
    

---

Смотрите также файлы

• практическое задание 2.docx

• Отчет по учебной практике о. 01(У) учебная практика, ознакомительная практика (в том числе получение первичных навыков.doc

• Политическая партия объединяет .doc

• Тест сратары Бірыай бітеу буынды сзді табыыз.docx

• Кроссворд ГРИБЫ И РАСТЕНИЯ.docx