ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИ



МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ

РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение

высшего образования
«САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ»

Кафедра общей и технической физики
ОТЧЁТ

по лабораторной работе №17

По дисциплине ФИЗИКА

(наименование учебной дисциплины согласно учебному плану)

Тема: Определение коэффициента теплопроводности газа

методом нагретой нити



Выполнил: студент гр. ГРП-22 Мурин В.Д.

(подпись) (Ф.И.О.)

Проверил:

(должность) (подпись) (Ф.И.О.)

Санкт-Петербург

2023 год

Цель работы: определить коэффициент теплопроводности воздуха методом нагретой нити при атмосферном давлении и различных температурах поверхности вертикальной цилиндрической трубки.

Краткое теоретическое содержание

Явление, изучаемое в работе: явление переноса энергии между молекулами газов (явление теплопроводности)

Определения (основных физических понятий, процессов, объектов и величин):

1. 
   Поток любой физической величины — это её количество, переносимое в единицу времени через воображаемую поверхность, перпендикулярно направлению переноса.
   
2. 
   Плотностью потокафизической величины называется ее количество, переносимое в единицу времени через единичную площадку, перпендикулярно направлению переноса.
   
3. 
   Теплопроводность – это процесс передачи теплоты от более нагретого слоя газа к менее нагретому, за счет хаотичного теплового движения молекул.
   
4. 
   Поток тепла - количество теплоты, проходящее в единицу времени через произвольную изотермическую поверхность.
   
5. 
   Градиент температуры – характеристика, показывающая направление наискорейшего возрастания температуры в зависимости от направления среды.
   
6. 
   Коэффициент теплопроводности - физическая величина, характеризующая и численно равная плотности потока энергии при градиенте температуры равном единице.
   

---

Законы и соотношения (использованные при выводе расчетной формулы):

1. 
   Закон Фурье:
   

Выравнивание температуры в системе сопровождается потоком тепла, плотность которого пропорциональна градиенту температуры в данной точке.

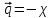grad T

где q  тепловой поток, Дж; 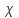- коэффициент теплопроводности, Вт/(м∙К); grad T - градиент температуры

2. 
   Закон Джоуля-Ленца:
   

Количество тепла, выделяемого в проводнике, прямо пропорционально квадрату

силы тока, сопротивлению проводника и времени его прохождения:



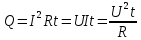
где Q – количество тепла, выделяемого в проводнике, Дж; I – сила тока в проводнике, А; R – сопротивление проводника, Ом; U – напряжение, приложенное к проводнику, В; t – время прохождения тока в проводнике, с;

Схема установки



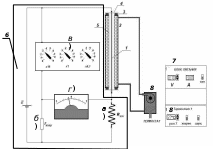
Схема:

1) Нить

2) Трубка

3) Упоры

4) Упоры

5) Трубка

6) Измерительный мост Уинстона

7) Пульт управления

а) Эталонный резистор

б) Нагревательный резистор

в) Магазин резисторов

г) Гальванометр

8) Термостат

Основные расчётные формулы:

1) Коэффициент теплопроводности:



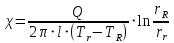
где 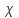- коэффициент теплопроводности, Вт/(м∙К); Q- поток тепла, Дж; l- длина цилиндра, м; T_r- температура газа у поверхности проволоки, К; T_R- температура газа у поверхности цилиндра, К; r_R- радиус цилиндра, м; r_r- радиус проволоки, м.

2) Поток тепла:

---

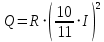
где Q- поток тепла, переносимый воздухом с проволоки, Дж; I- сила тока в проводнике, А; R- сопротивление проводника, Ом.

3) Температура газа у поверхности проволоки:



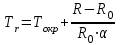
где Т_r - температура газа у поверхности нити, К; T_окр- температура окружающей среды, К; R - сопротивление проволоки, Ом; R₀ – сопротивление проволоки при комнатной температуре, Ом;  - коэффициент температурного сопротивления, Ом/град.

4) Среднеарифметическая температура



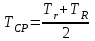
где T_ср  среднеарифметическая температура, К; T_r  температура газа у поверхности нити, K; T_R  температура газа у поверхности цилиндра, K.

5) Зависимость электрического сопротивления от температуры



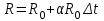
где R - сопротивление проволоки, Ом; R₀ – сопротивление проволоки при комнатной температуре, Ом;  - коэффициент температурного сопротивления, 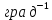; Δt - разность температур газа у поверхностей проволоки T_r и цилиндра T_R.

Формулы погрешностей косвенных измерений:




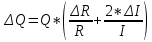
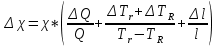
Таблица №1. Результаты измерений и вычислений

Физ. величина	ТR	U	I	R
Ед. измерения Номер опыта	К	В	А	Ом
1	293	1	0,15	3,885
2	293	2	0,29	4,06
3	293	3	0,42	4,35
4	293	4	0,54	4,72
5	293	5	0,64	5,15

---

Табл.1.Результаты измерений и вычислений

Таблица №2. Определение коэффициента теплопроводности



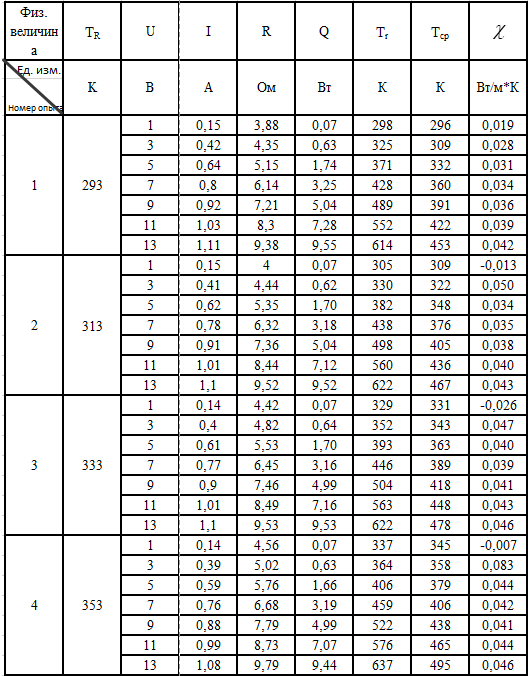
Табл.2 Определение коэффициента теплопроводности

Исходные данные:

диаметр проволоки 0,1*10^-3 м;

внутренний диаметр цилиндра 8 *10^-3 м;

длина проволоки 0,5 м;

материал проволоки вольфрам;

коэффициент температурного сопротивления

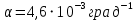
Погрешности прямых измерений:

∆U = 1 В, ∆I = 0,01 A, ∆R = 0,01 Ом, ∆T_R = ∆T_r = 0,1К,

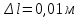
Примеры вычисления:

1. 
   Поток тепла, переносимый воздухом
   

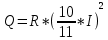
Q=3,38*(10/11*0,15)²=0,07 Дж

2. 
   Температура газа у поверхности нити
   

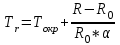
T_r=293+(3,88-3,79)/ (3,79*4,6*10^-3) =298К

3. 
   Среднеарифметическая температура
   

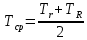
T_cp= (293+298)/2=296К

4. 
   Коэффициент теплопроводности
   

5. 
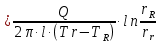
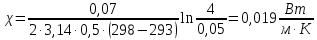
   Погрешность косвенных измерений
   

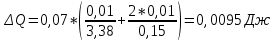
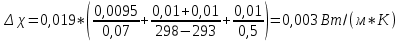
Окончательный результат:



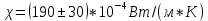
Графический материал

График зависимости



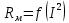
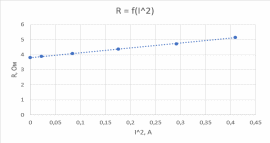
Из графика находим значение R_o равное примерно 3,79 Ом.

_{График зависимости}

---

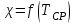
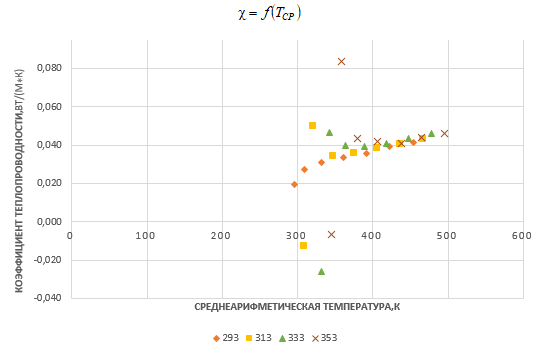
Вывод

В ходе лабораторной работы был определен коэффициент теплопроводности воздуха при атмосферном давлении и разных температурах по теплоотдаче, нагреваемой током нити в цилиндрическом сосуде, равный 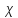= (190±30) *10^-4 Вт/(м*К). Это связано с тем, что при увеличении потока тепла и температуры газа у поверхности проволоки, коэффициент теплопроводности увеличивается. Относительная погрешность составила ɛ = 30/190 *100% = 15%. Расхождение теоретических и экспериментальных значений: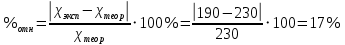



Из-за неточности приборов экспериментально полученное значение отличается от теоретического на 17%.

---

Смотрите также файлы

• Тема Аппаратное обеспечение иттехнологий.pdf

• Правила допуска к написанию итоговой работы.doc

• Наше сердце.docx

• Блім 4а органикалы химияа кіріспе.docx

• Приказ от 20 г.0107 План проведения мероприятий, посвященных празднованию Дня победы, запланированных гбоу нао сш с. Несь.docx