Файл: Тема Нормальные формы. Понятия тупиковой, минимальной и сокращенной днф. Методы получения сокращенной и минимальной днф.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 30
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Практическое задание 5
Тема 4.3. Нормальные формы. Понятия тупиковой, минимальной и сокращенной ДНФ. Методы получения сокращенной и минимальной ДНФ
Формулировка задания 4
Для данных функций
 и
и 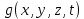 , заданных векторно в табл. 5.1, проделать следующее.
, заданных векторно в табл. 5.1, проделать следующее.1. Записать их СДНФ и СКНФ.
2. Методом Квайна найти сокращенную ДНФ.
3. Для сокращенной ДНФ построить матрицу Квайна, указать ядровые импликанты.
4. С помощью матрицы Квайна найти минимальную ДНФ, указать ее сложность.
5. Найти минимальную ДНФ данной функции с помощью карт Карно, сравнить полученный результат с ДНФ, найденной в п. 4.
Таблица 5.1
| № | f | g |
| 1 | 1011 1100 | 1111 0101 0011 1101 |
| 2 | 0111 1010 | 1101 1110 1010 1110 |
| 3 | 1001 1001 | 0111 0001 1111 1101 |
| 4 | 1110 1110 | 1011 1111 1111 1000 |
| 5 | 1010 1111 | 1101 0101 1101 1111 |
| 6 | 0110 1111 | 1111 1110 1010 0011 |
| 7 | 1000 0110 | 111 0010 0111 1110 |
| 8 | 0111 0110 | 1100 1110 1111 1011 |
| 9 | 1110 0110 | 1100 0110 1111 0111 |
| 10 | 0111 1110 | 1011 1111 1110 0010 |
Рекомендации по выполнению задания
Номер варианта задания вы можете определить, используя табл. 5.2, по первой букве вашей фамилии. Решение расписывать как можно подробнее, описывать формулы, которыми пользуетесь во время решения, – обязательно. Обязательно должно быть записано условие задания, ответ.
Таблица 5.2
Выбор варианта задания
| Буква | А, Ф, Э | Б, М, Х | В, Ю | Г, У,Я | Д, Ч, С | Е, Н, П | Ж, О, З | И, Ц | К, Т, Ш, Щ | Л, Р |
| № вар. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Указания по выполнению работы
Для данных функций
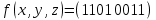 и
и 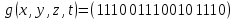 , заданных векторно, проделать следующее:
, заданных векторно, проделать следующее:1. Записать их СДНФ и СКНФ.
2. Методом Квайна найти сокращенную ДНФ.
3. Для сокращенной ДНФ построить матрицу Квайна, указать ядровые импликанты.
4. С помощью матрицы Квайна найти минимальную ДНФ, указать ее сложность.
5. Найти минимальную ДНФ данной функции с помощью карт Карно, сравнить полученный результат с ДНФ, найденной в п. 4.
Решение
Распишем таблицы истинности функций.
|
|
-
СДНФ:
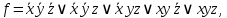
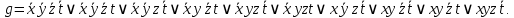
СКНФ:
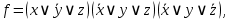
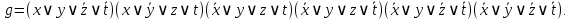
2. Найдем сокращенную ДНФ из записанной СДНФ. Для более легкого восприятия символы переменных заменим на показатели степеней переменных. Например, вместо
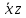 будем употреблять набор 0-1-. В этом случае СДНФ булевой функции будет соответствовать множество всех ее единичных наборов (т. е. тех наборов, на которых функция принимает значение 1). Выпишем единичные наборы данной булевой функции в таблицу, разбив их на группы в соответствии с количеством единичных компонент в наборах.
будем употреблять набор 0-1-. В этом случае СДНФ булевой функции будет соответствовать множество всех ее единичных наборов (т. е. тех наборов, на которых функция принимает значение 1). Выпишем единичные наборы данной булевой функции в таблицу, разбив их на группы в соответствии с количеством единичных компонент в наборах.Тогда для применения формулы склеивания достаточно просмотреть всевозможные пары наборов, входящих в соседние группы.
| 0 0 0 + | 0 0 – |
| 0 0 1 + | |
| 0 – 1 | |
| 0 1 1 + 1 1 0 + | |
| 1 1 1 + I полоса | |
| 1 1 – II полоса |
Сокращенная ДНФ данной булевой функции имеет вид:
 .
.| 0 0 0 0 + | 0 0 0 - 0 0 – 0 | |
| 0 0 0 1 + 0 0 1 0 + | ||
| 0 – 1 0 + - 0 1 0 + | - - 1 0 - - 1 0 | |
| 0 1 0 1 + 0 1 1 0 + 1 0 1 0 + 1 1 0 0 | ||
| - 1 – 1 - 1 – 1 - 1 1 – - 1 1 – 1 1 - - 1 1 - - III полоса | ||
| 0 1 1 1 + 1 1 0 1 + 1 1 1 0 + | ||
| 0 1 – 1 + - 1 0 1 + 0 1 1 – + - 1 1 0 + 1 – 1 0 + 1 1 0 – + 1 1 – 0 + | ||
| 1 1 1 1 + I полоса | ||
| - 1 1 1 + 1 1 – 1 + 1 1 1 - + II полоса |
Сокращенная ДНФ данной булевой функции имеет вид:
 .
.3. Для получения из сокращенной ДНФ минимальной ДНФ изобразим следующую таблицу – матрицу Квайна.
|
 |
4. Для функции f все три импликанты являются ядровыми (если в строке одна единица, то выделяем ее и столбцы с выделенными единицами дают ядровые импликанты). Поэтому сокращенная ДНФ является и минимальной, ее сложность равна шести.
Для функции g
 ядровыми импликантами являются 1, 3, 4 и 6. Отметим все строки, перекрываемые этими импликантами, знаком +. В результате получили, что ядровые импликанты обеспечивают единицы во всех строках и, значит, только они образуют минимальную ДНФ:
ядровыми импликантами являются 1, 3, 4 и 6. Отметим все строки, перекрываемые этими импликантами, знаком +. В результате получили, что ядровые импликанты обеспечивают единицы во всех строках и, значит, только они образуют минимальную ДНФ:  , ее сложность равна девяти.
, ее сложность равна девяти.5. Найдем минимальную ДНФ с помощью карт Карно.
Максимальный размер прямоугольников равен двум, чтобы покрыть все единицы, требуется три прямоугольника. Запишем импликанты для каждого треугольника. Первый прямоугольник дает импликанту  (единицы стоят в таких позициях, которые отличаются значениями z, а переменные x и y принимают значения нуль). Второй прямоугольник – (единицы стоят в таких позициях, которые отличаются значениями z, а переменные x и y принимают значения нуль). Второй прямоугольник –  , третий – , третий –  . В результате мы получили минимальную ДНФ, . В результате мы получили минимальную ДНФ,  , сложность которой равна шести. Эта полученная минимальная ДНФ отличается от полученной в пункте 4. Это связано с тем, что мы второй прямоугольник могли нарисовать не вертикальным, а горизонтальным. Самое главное, что сложности полученных ДНФ одинаковые. Этот пример еще раз подтверждает тот факт, что можно получить различные формулы для ДНФ, но все они будут иметь одинаковую сложность , сложность которой равна шести. Эта полученная минимальная ДНФ отличается от полученной в пункте 4. Это связано с тем, что мы второй прямоугольник могли нарисовать не вертикальным, а горизонтальным. Самое главное, что сложности полученных ДНФ одинаковые. Этот пример еще раз подтверждает тот факт, что можно получить различные формулы для ДНФ, но все они будут иметь одинаковую сложность |
Рассмотрим возможные способы для изображения прямоугольников. Синим цветом выделены единицы, для которых существует единственный способ для образования прямоугольников. В результате все нарисованные для этих единиц прямоугольники покрыли и все остальные треугольники. Запишем импликанты для каждого треугольника. Первый прямоугольник дает импликанту  . Второй прямоугольник – . Второй прямоугольник –  , третий – , третий –  , четвертый – , четвертый –  Минимальная ДНФ: Минимальная ДНФ:  , совпадает с полученной в пункте 4 , совпадает с полученной в пункте 4 |
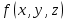
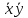


 1
1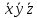
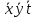
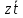
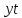

 yz
yz
 12
12 1
1 1
1