========================================================

З А Д А Ч А N 1

Дана последовательность однополярных прямоугольных импульсов с амплитудой Е [В] и длительностью Т_i [с].

Период последовательности Т кратен Т_i.

Определите:

1. Уровень постоянной составляющей спектра последовательности U_o.

2. Амплитуду n-ой гармоники A_n.

3. Расстояние между соседними спектральными составляющими (вдоль оси частот) df.

4. Минимальный номер гармоники N₁, амплитуда которой равна нулю.

5. Значение частоты гармоники с минимальным номером N₁, амплитуда которой равна нулю.

==================================================================

Решение задачи:

Любая периодическая функция u(t) с периодом Т может быть представлена рядом Фурье:

.

1. Постоянная составляющая последовательности определяется выражением:

,

Так как за пределами интервала времени t₁- t₂ значения последовательности равны нулю, то пределы интегрирования можно изменить:

.

2. Амплитуда n-ой гармоники определяется следующим образом:

,

где a_n и b_n– коэффициенты ряда Фурье:

Если функция u(t) – четная, то коэффициенты b_n в ряде Фурье равны нулю.

Сместим ось времени в нашей последовательности так, чтобы она стала четной функцией:

В этом случае It₁I = t₂ = T_i/2.

Известно, что . Поэтому можно записать:

.

Спектрограмма периодической последовательности прямоугольных импульсов

A_n

f

0

3. Так как f_n = n/T, то между соседними составляющими спектра расстояние по оси частот равно df =1/T [Гц].

4. . A_n= 0 при условии, что , т. е. когда выполняется условие . Если k = 0, то n = 0 и имеет место отношение sin(0)/0, которое является неопределенностью, раскрываемой по правилу Лапиталя:

.

С учетом этого k ≠ 0. Следующее минимальное целое значение k = 1.

Тогда и n = T/T_i(это скважность данной периодической последовательности прямоугольных импульсов).

5. Частота гармоники наименьшего порядка, у которой амплитуда равна нулю имеет следующее численное значение: f_n = ndf = 1/T_i.

О

1. ;

2. ;

3. df = 1/T;

4. n=T/T_i;

5. f_n=1/T_i.

тветы:

З А Д А Ч А N 2

Видеоимпульс описывается функциональным выражением

U(t) = U_o[ (t + T/2) - (t - T/2)],

где (t) - функция Хевисайда

Определите:

1. Спектральную плотность S(f) этого видеоимпульса на частоте f = 0.

2. Спектральную плотность S(f) этого видеоимпульса на частоте f = 1/(2T)

3. Укажите наименьшее значение частоты f₁, на которой спектральная

плотность равна нулю.

Решение:

Формула для вычисления спектральной плотности:

где - цикл частоты,

Так как вне интервала U(t) =0, то изменим пределы интегрирования:

По формуле Эйлера:

1) При f=0 S(t)=0/0 – неопределенность. При x->0 sinx = x по свойству эквивалентных БМФ:

2)

3)

Мы имеем 2 варианта:

а) , что не верно, т.к. по 1)

б)

О

1. ;

2.

тветы:

З А Д А Ч А N 3

Модуль спектральной плотности импульсного сигнала представляет собой

П-образную функцию частоты с уровнем S_o [В/Гц] в пределах от -F_o до +F_o [Гц] и равную нулю за пределами этого интервала частот.

---

Фазовый спектр этого импульсного сигнала равен нулю.

Определите:

1. Максимальное значение импульсного сигнала U_max.

2. Длительность T_i импульсного сигнала, которая оценивается интервалом времени между двумя его минимальными значениями, одно из которых предшествует максимуму, а второе следует за максимумом.

3. Значение импульсного сигнала на расстоянии t = T_i / 4 от его максимума.

========================================================

Решение:

Формула ОПФ:

Так как S(t)=0 вне интервала , изменим пределы интегрирования.

По формуле Эйлера:

Получим:

Приведём к виду sinC-функции :

1) Значение sinc-функции максимально в точке t=0, поэтому по правилу Лапиталя заменим на

2) , т.к. в точках sinc=0 (минимум)

а) ,

б) ,

3)

Из пункта 2)

О

1. ;

2.

тветы:

========================================================

З А Д А Ч А N 4

Вольт-амперная характеристика диода I_g(U_g) [mA] аппроксимирована кусочно-линейной функцией :

I_g = K  U_g для U_g > 0;

I_g = 0 для U_g ≤ 0.

На диод подано смещение U_o [B] и гармоническое колебание с амплитудой A [B].

Определите:

1. Амплитуду косинусоидальных импульсов тока диода I_m [mA].

2. Угол отсечки косинусоидальных импульсов тока диода Q [радиан].

3. Амплитуду 1-ой гармоники косинусоидальных импульсов тока диода I₁ [mA].

Формулы для расчета коэффициентов Берга:

₁(Q) = (Q - sin(Q)  cos(Q)) / π ₁(Q) = ₁(Q) / (1 - cos(Q))

Решение:

1. Отрицательное смещение: <0

1) Для Uд>0 Iд=KUд; где

2) Зависимость между θ и определяется как

3) Для определения амплитуды 1-й гармоники воспользуемся коэффициентом Берга 1-го порядка:

2. Положительное смещение диода:>0

1)

2)

3)

1.;

2.

Ответы:

========================================================

З А Д А Ч А N 5

Несущая сигнала с амплитудой A₁₀ [В] и с частотой f_o [Гц] модулирована

по амплитуде гармоническим колебанием низкой частоты F [Гц].

Коэффициент модуляции равен М₁. Это колебание подано на вход одноконтурного резонансного усилителя c коэффициентом усиления К, настроенного на частоту несущей сигнала.

На выходе усилителя имеет место амплитудно-модулированное колебание с коэффициентом модуляции М₂ = 0.707  М₁.

Определите:

1. Амплитуду боковой спектральной составляющей на входе усилителя A₁₁.

2. Амплитуду несущей на выходе усилителя A₂₀.

3. Амплитуду боковой спектральной составляющей на выходе усилителя A₂₁.

4. Добротность резонансного контура усилителя Q.

========================================================

РЕШЕНИЕ:

В спектре амплитудно-модулированных колебаний сигнала содержится 3 спектральных составляющих:

- одна распределена на частоте несущей и имеет амплитуду несущего колебания ;

- две другие (боковые) расположены слева и справа от частоты несущего колебания на расстоянии, равном частоте модулирующего колебания F и имеют амплитуду:

1. Коэффициент усиления усилителя равен K. Тогда соответственно:

2. Амплитуды боковых спектральных составляющих на выходе зависят от коэффициента амплитудной модуляции на выходе, который равен:

---

и амплитуды несущей на :

Для определения добротности воспользуемся формулой:

Где - частота несущей, - полоса пропускания.

Ответ:

1)

2)

3)

4)

==================================================================

З А Д А Ч А N 6

Фильтр нижних частот (ФНЧ) имеет П-образную амплитудно-частотную характеристику, которая равна К_а во всей полосе пропускания частот от -F_o до +F_o [Гц].

Будем считать, что фазо-частотная характеристика Ф(ω) этого идеализированного фильтра линейно зависит от частоты:

Ф(ω) = - K_ф  ω

На вход этого фильтра подается короткий импульс u(t) = U_o  (t),

где  (t) - функция Дирака.

Определите:

1. Максимальное значение сигнала U_max на выходе ФНЧ.

2. Длительность T_i сигнала на выходе ФНЧ, которая оценивается интервалом

времени между двумя его минимальными значениями, одно из которых

предшествует максимуму, а второе следует за максимумом.

3. Значение импульсного сигнала на расстоянии t = T_i / 4 от его максимума.

4. Время задержки T_з местоположения U_max сигнала на выходе ФНЧ по
отношению к моменту воздействия дельта-импульса на его входе.

===================================================================

Решение:

Рисунок – АЧХ и ФЧХ сигнала

Сигнал на выходе Sвых(t) находится:

Чтобы найти воспользуемся фильтрующим свойством -функции:

Если непрерывную функцию умножить на -функцию и проинтегрировать её по времени, то мы получим значение функции в точка, где сосредоточен ????-импульс:

???? – обобщённая функция, позволяющая описать точечное воздействие, а также пространственную плотность физических величин.

В нашем случае:

1. Применим обратное преобразование Фурье (ОПФ) для восстановления сигнала:

Изменим предел интегрирования и подставим известные величины:

Применим формулу Эйлера:

Приведём к sinc-функции:

Максимальное значение будет в том случае, если . Следовательно, возникает неопределённость вида sinc(φ) при φ⇒0 = 0/0.

Раскрываем по правилу Лапиталя:

2. В точках t1 и t2 sinc-функция равна нулю. Ti = t2-t1

А)

Б)

3.

Из пункта 2:

Следовательно:

4.

Ответ:

1.

2.

3.

4.

===================================================================

З А Д А Ч А N 7

Сигнальное устройство представляет собой высокочастотный усилительный тракт, линейный двухполупериодный детектор, решающее устройство и звуковой индикатор. Если на выходе линейного детектора напряжение U(t) превышает порог U_o, который имеет решающее устройство, то возникает звуковой сигнал тревоги.

В дежурном режиме на входе усилительного тракта присутствует гауссовский шум. При этом на выходе линейного детектора напряжение имеет распределение Рэлея:

p(U) = (U / s²) exp(-U² /(2  s² ));

Определите вероятность того, что в заданный момент времени при работе сигнального устройства в дежурном режиме возникнет сигнал ложной тревоги P_лт.

===================================================================

Решение: на выходе усилительного тракта (в точке 1) присутствует гауссовский шум:

Он имеет нормальное распределение:

---

В точке 2 все значения U>0 отсекаются и имеет место одностороннее нормальное распределение:

После ФНЧ сигнал имеет распределение Релея:

Сигнал тревоги срабатывает при U(t)> . Следовательно, чтобы найти вероятность ложной тревоги, нужно найти площадь заштрихованной фигуры на графике распределения Релея, то есть:

С учётом:

Получим:

Ответ:

З А Д А Ч А N 8

Амплитуда несущего колебания на выходе передатчика равна U_o [B].

На передатчике осуществляется частотная модуляция гармоническим колебанием.

При этом мгновенная частота сигнала изменяется по закону

f(t) = f_o + ∆F  cos(2πFt + θ),

где f_o - частота несущего колебания,

∆F - девиация частоты,

F - частота модулирующего колебания,

θ- начальная фаза модулирующего колебания.

Определите амплитуду A_o компонента спектра колебания на выходе передатчика на частоте несущей, а также амплитуду 1-ой составляющей верхней A_1h (или нижней A_1l) боковой частоты .

==================================================================

Решение: сигналы с угловой модуляцией описываются выражением:

Где

В данном случае:

Найдём

Так как обе функции периодические, они могут быть представлены в виде рядов Фурье, полученных в теории функции Бесселя.

Следовательно, амплитуда n-й составляющей спектра ЧМ-сигнала по отношению к нулевому компоненту на частоте равна произведению амплитуды несущего колебания на функцию Бесселя соответствующего порядка.

В условии данной задачи будем рассматривать функции Бесселя 0 и 1 порядков.

Спектр ЧМ-сигнала:

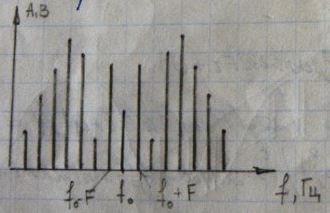
Ответ:

З А Д А Ч А N 9

Амплитудно-модулированное колебание вида

s₁(t) = A_o(1 + M  cos(2πFt))  cos(ωt)

подано на квадратичный детектор с характеристикой

U_вых = К  (U_вх)².

Определите на выходе этого детектора уровень постоянного напряжения U_2o и амплитуды A(F) и A(2F) составляющих спектра с частотами соответственно
F и 2F.

Решение:

Определим U_вых:

По формуле понижения степени:

– т.к. этот множитель даёт высокочастотные составляющие, которые отсекаются, то выражение считается: . Тогда:

Ответ:

1. Постоянное U_вых:

2. Полученный сигнал:

3. 2-я гармоника полезного сигнала, являющаяся результатом искажения сигнала из-за квадратичности спектра:

З А Д А Ч А N 10

Континуальный сигнал, спектр которого занимает полосу частот равную ∆F, стробируется последовательностью коротких прямоугольных импульсов, имеющих длительность T_i. Полученные отсчеты передаются по линии связи, полоса пропускания которой считается неограниченной.

На приемной стороне континуальный сигнал восстанавливается посредством
П-образного фильтра нижних частот, имеющего полосу пропускания ∆F.

Определите максимальное значение T_max периода последовательности прямоугольных импульсов, при котором принятый сигнал будет полностью восстановлен. Какое предельное число корреспондентов M_max может одновременно передавать информацию по каналу связи при применении временного уплотнения.

---

==================================================================

Решение:

По теореме Котельникова, произвольный сигнал может быть полностью восстановлен, если известны отсчётные значения этого сигнала, взятые через равные промежутки времени (1/2f), где f – наивысшая частота спектра.

1. Максимальное значение T_max периода последовательности прямоугольных импульсов, при котором принятый сигнал будет полностью восстановлен:

2. Число корреспондентов M_max может одновременно передавать информацию по каналу связи при применении временного уплотнения:

---

Смотрите также файлы

• Листинг кода домашних работ 3 варианта на языке С#.docx

• учебное пособие.doc

• Введение в теорию систем.pdf

• Модели с равномерным наполнением запаса с дефицитом.docx

• Проблема оптимизации при принятии решения.pdf