МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «ТЮМЕНСКИЙ ИНДУСТРИАЛЬНЫЙ УНИВЕРСИТЕТ» Институт промышленных технологий и инжиниринга Кафедра переработки нефти и газа КОНТРОЛЬНАЯ РАБОТА По дисциплине «Основы научных исследований и проектирования» (вариант №6) Выполнил: Проверил: Таранова Л. В. к.т.н., доцент Тюмень ТИУ 2023

1.1. Оценка ошибок измерений

Целью аналитических определений является получение значений, наиболее близких к истинному содержанию определяемой величины. Поэтому задачей каждого измерения является получение результата и оценка его точности. Для этих целей любое измерение выполняется несколько раз и точность оценок измерений тем выше, чем больше число измерений (объем выборки). При проведении исследований результаты определений должны быть близки так. Чтобы можно было говорить о их воспроизводимости.

Для оценки ошибки измерения введем ключевые понятия и рассмотрим основные расчетные формулы:

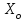- истинное значение измеряемой величины;

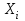- измеряемое в i – опыте значение;

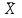- среднее арифметическое значение всех измерений;

- абсолютное отклонение каждого измерения от среднего значения (или ошибка конкретного измерения);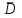

= среднее отклонение или средняя ошибка;

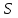- среднее квадратичное отклонение (или стандартное отклонение);

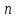- число измерений.

Среднее арифметическое значение

---

выборки вычисляется по формуле:




Одним из способов выражения точности измерений является указание абсолютной величины отклонения результата измерения:

















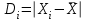
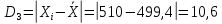
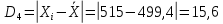
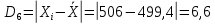
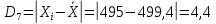
Так как истинное значение величины можно оценить лишь по среднему из измеряемых значений, то ошибку при определении указанной величины можно выразить после усреднения отклонений всех измеряемых значений.





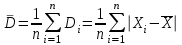
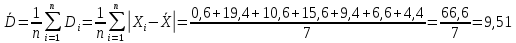
Средняя и абсолютная ошибки имеют размерность определяемой величины или выражаются в процентах.

Например, при определении высокотемпературной вязкости моторного масла получены следующие значения: Х = 125 Мпа*с; Д = +5Мпа*с. Тогда результат записывают следующим образом;

Х=125_ +5 Мпа*с

Среднее отклонение (в %) рассчитывают следующим образом:



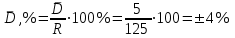
Следовательно, точность определения вязкости составила 4%.

В стандартных методиках обычно указывается точность определения того или иного показателя (2, 3 или 5%). При выполнении любых анализов необходимо определять ошибку метода.

Стандартное отклонение. Точность результатов измерений чаще всего выражают с помощью стандартного отклонения (S), которое представляет собой квадратный корень из второго момента распределения относительно среднего значения и находится по формулам:

---

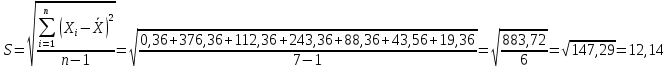
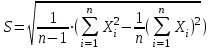
При записи значения измеряемой величины учитывают стандартное отклонение среднего арифметического, т.е.:





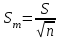
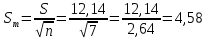
Число результатов, которое характеризуется отклонением от среднего на величину не более 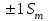составляет 68,26%; 95,46% измерений характеризуются отклонениями, не превышающими 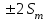и 99,73% - отклонениями, не превышающими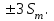

Когда число измерений не велико ( <30), значения величины S претерпевают значительные флуктуации и распределение результатов уже не подчиняется стандартному, нормальному закону Гаусса. Чтобы в таких случаях вычислить пределы доверительности для произвольной вероятности (не только 1S, 2S и т.д.), применяют t-значение, которое является поправочным коэффициентом, вводимым в величину S (определяется из t-распределения Стьюдента) (Приложение 2).

Окончательный результат записывается следующим образом:

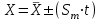
№ п/п				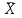				(Х – Х )2			S		m
1	500	499,4		0,6		9,51		0,36			12,14		4,58
2	480		499,4		19,4		9,51		376,36	12,14		4,58
3	510		499,4		10,6		9,51		112,36	12,14		4,58
4	515		499,4		15,6		9,51		243,36	12,14		4,58
5	490		499,4		9,4		9,51		88,36	12,14		4,58
6	506		499,4		6,6		9,51		43,56	12,14		4,58
7	495		499,4		4,4		9,51		19,36	12,14		4,58
∑	3496				66,6				883,72

---

Определим значение измеряемой величины, с использованием среднего и стандартного отклонения:

а) По среднему отклонению получим:

Х =499,4+_ 9,51;

б) По стандартному отклонению для надёжности 68%:

Х= 499,4+_ 4,58;

Т.е. в 68% случаев значение измеряемой величины окажется в пределах между 494,82 и 503,98;

в) Для надёжности 95% значение измеряемой величины составит:

Х= 499,4 +_4,58*t,

где t –критерий Стьюдента; по данным таблице 1 в приложении получим: t=2,447

Тогда Х =499,4 +_4,58*2,447=499,4+_11,21,

Т.е. в 95% случаев значение измеряемой величины будет находиться между 488,19 и 510,61

1.2. Оценка достоверности результатов измерений (отбрасывание малоправдоподобных данных)

В тех случаях, когда среди результатов измерений одно значение существенно отличается от всех остальных или от среднего значения, необходимо принять решение относительно учета этого аномальное значение или отбросить его как малоправдоподобное. Для принятия решения можно воспользоваться одним из 4^Х методов, рассмотренных ниже.

1). Метод «четырех ». В этом методе используется введенное понятие о среднем отклонении .

Порядок проверки:

-Вычисляем среднее арифметическое серии (Х) и среднее отклонение (Д)

-Находим сомнительный результат Х_сомн

-Отбрасываем малоправдоподобное значение и вычисляем по оставшимся результатам данной серии новое среднее значение 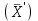и новое среднее отклонение .

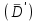-Вычисляем значение .

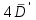-Определяем разницу между сомнительным значением и новым средним .

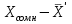-Если результат сомнительного значения отличается от нового среднего значения более, чем на 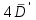, то его отбрасывают как малоправдоподобный.

Этот метод обеспечивает приблизительно 99%-ую вероятность того, что отбрасывание подозрительного значения оправдано (если число данных 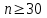). Столь высокий доверительный уровень (99%) нередко совсем не обязателен и его можно применять и при меньшем числе измерений.

---

Рассмотрим примериспользования метода.

Пример: Имеем следующую серию результатов измерений:

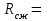500; 480; 510; 515; 490; 506; 495

• 
  Сомнительным результатом является значение 480, 515
  
• 
  Определяем среднее арифметическое без величины 480; 515 и среднее отклонение ; результаты сведем в таблицу:
  

	500	510	490	506	495
	0,2	9,8	10,2	5,8	5,2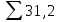

• 
  Определим искомые значения:
  

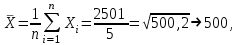
Находим

• 
  Находим разницу между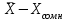 , т.е. 500-480=20
  
• 
  Сравниваем значение с величиной , т.е 20 < 24,8 и делаем вывод:
  
• 
  Так как разница меньше, чем , то сомнительное значение 480 следует оставить.
  
• 
  Находим разницу между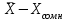 , т.е. 500-515=15
  
• 
  Сравниваем значение с величиной , т.е 15 < 24,8 и делаем вывод:
  
• 
  Так как разница меньше, чем , то сомнительное значение 515 следует оставить.
  

---

Смотрите также файлы

• Правила внутреннего трудового распорядка работников муниципального казенного общеобразовательного учреждения Ихрекская средняя общеобразовательная школа.pdf

• Программа технической направленности робототехника.docx

• Лекция 22. Элементы физики лазеров 22 Спонтанные и вынужденные переходы.doc

• Мой дед уходил на войну, За Родину шел воевать.docx

• Литература, используемая при проведении занятия Учебник спасателя С. К. Шойгу Основы доврачебной помощи М. 89.docx