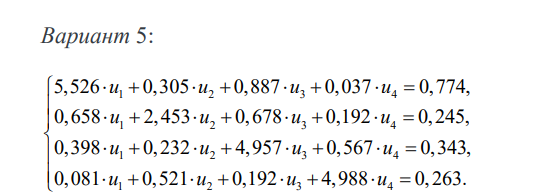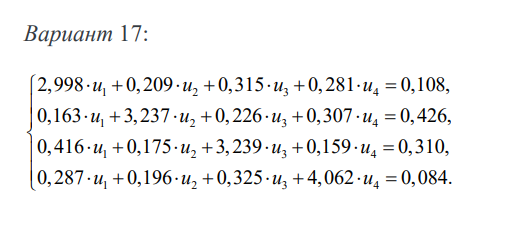Файл: Дана система линейных алгебраических уравнений (слау).docx

Сделать презентацию

Скачать файл (0,15Мб)

Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 11.01.2024

Просмотров: 82

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Дана система линейных алгебраических уравнений (СЛАУ)

Auf, (1)

^^a11

^a12

^a13

^a14 ^

 ^u¹

 ^f¹

     

где

_A_^^a21 ^a22

^a23 ^a24 ^_,

u  ^^u²^^,f  ^^f²^^.

^a a

a a ^

 _u  _f

_31 32

33 34 _

 ³  ³

^a a

a a ^

 _u  _f

 41 42

43 44 

 4   4 

Решить СЛАУ (1) методом Гаусса с выбором главного элемента по столбцам.
Привести СЛАУ (1) к виду

u  Bu  F ,

приемлемому для применения метода простой итерации, и проверить выполнение достаточного условия сходимости этого метода, т. е.

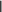
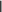B  q1, (2)

где

B  E  A ,
F   f ,

 ¹^{0 0}



 ₀
_E__0 1 0

_0 1

_0 0 0

⁰



₀
⁰^, значение  выбрать таким, чтобы



1_

выполнялось неравенство (2).

Решить эту СЛАУ методом простой итерации
u_k_₁ Bu_k F

с точностью   0,01 , предварительно преобразовав ее к виду, приемлемому

для применения этого метода. В качестве начального приближения выбрать

^u⁰^⁰^,^где⁰^^0,^0,^0,⁰ ^.

T

В качестве условия остановки итерационного процесса (для достижения заданной точности  ) использовать неравенство

^uk1 ^^uk

 1 q , (3)

где q– константа из неравенства (2). Имеет место неравенство

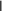
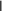
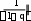ε_k

^uk1 ^^uk ^,

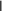где

ε_k u_k U , U – вектор точного решения СЛАУ,

^uk1 ^и^uk

векторы

^{приближенного}^{решения}^СЛАУ,^{полученные}^наk1^-й^иk^-й^{итерациях}соответственно. Следовательно, если выполняется неравенство

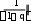^uk1 ^^uk

  ^,

равносильное неравенству (3), то справедливо и неравенство

ε_k  ,

обеспечивающее нахождение вектора u_k

заданной точностью  .

приближенного решения СЛАУ с

В качестве нормы

^uk1 ^^uk

вектора

^uk1 ^^uk

взять октаэдрическую

норму, определяемую равенством

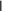
4 u₂ _u_ii1

^,^где^u^^u^1,^u²^,^u^3,^u⁴

T ^,

а в качестве нормы B матрицы ^B– норму, согласованную с октаэдрической

нормой вектора, определяемую следующим образом:

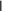
4B  max _

b, где

B  _b_4 .

²1 j4

ij

i1

^iji, j1

Смотрите также файлы

Игра как образовательный процесс и как творчество.docx

.docx

Культура общения педагога и учащегося.doc

Бизнеспланирование группа чу20М671 Студент С. Р. Колегова.docx

Опасные грузы классификация и характеристики опасные грузы.pptx

Файл: Дана система линейных алгебраических уравнений (слау).docx

Дана система линейных алгебраических уравнений (СЛАУ)

где

где

₀
⁰^, значение  выбрать таким, чтобы

выполнялось неравенство (2).

где q– константа из неравенства (2). Имеет место неравенство

где

векторы

равносильное неравенству (3), то справедливо и неравенство

обеспечивающее нахождение вектора u_k

приближенного решения СЛАУ с

вектора

взять октаэдрическую

Смотрите также файлы

Информация

Списки файлов

Дополнительно

Файл: Дана система линейных алгебраических уравнений (слау).docx

Дана система линейных алгебраических уравнений (СЛАУ)

где

где

00 , значение  выбрать таким, чтобы

выполнялось неравенство (2).

где q– константа из неравенства (2). Имеет место неравенство

где

векторы

равносильное неравенству (3), то справедливо и неравенство

обеспечивающее нахождение вектора uk

приближенного решения СЛАУ с

вектора

взять октаэдрическую

Смотрите также файлы

Информация

Списки файлов

Дополнительно

₀
⁰^, значение  выбрать таким, чтобы

обеспечивающее нахождение вектора u_k