ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 44
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ПЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ
ЗАВЕДЕНИЕ РОССИИ
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
САНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ
Кафедра механики
РАСЧЁТНО-ГРАФИЧЕСКАЯ РАБОТА №1
По дисциплине Теоретическая механика
(наименование учебной дисциплины согласно учебному плану)
Выполнил: студент гр.
(шифр группы) (подпись) (Ф.И.О.)
Оценка:
Дата:
Проверил
руководитель работы: доцент
(должность) (подпись) (Ф.И.О.)
Санкт-Петербург
2023
Исходные данные
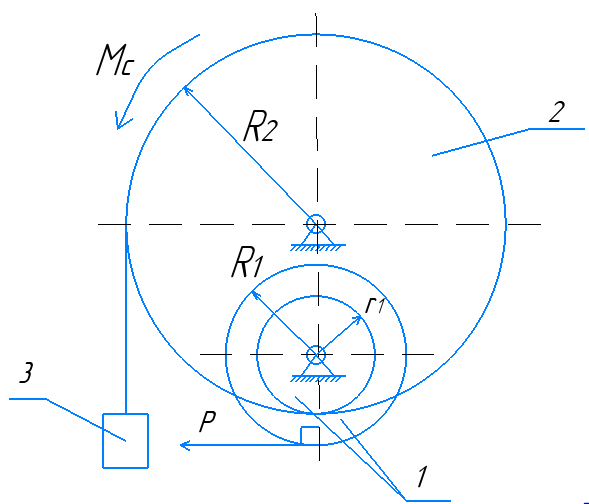
Рисунок 1 – Исходная схема изучаемой системы
Механическая система, состоящая из неоднородных дисков 1 и 2 и груза 3, начинает движение в вертикальной плоскости из состояния покоя под действием постоянной силы P. На диск 2 действует постоянный момент сил сопротивления Mc.
Определить скорость v3 груза 3 после его перемещения на расстояние s.
m1,m2, m3 – массы дисков 1 и 2 и груза 3, соответственно;
R1, r1, R2, r2 – радиусы больших и малых окружностей дисков 1 и 2, соответственно;
i1, i2– радиусы инерций дисков 1 и 2;
P – постоянная движущая сила;
Mc – постоянный момент сил сопротивления;
T0 – начальная кинетическая энергия данной системы (T0 = 0);
s – расстояние, пройденное грузом 3;
v3 – искомая скорость груза 3 в конечном положении механической системы.
Решение
Теорема об изменении кинетической энергии:
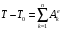, (1)где T – кинетическая энергия системы в конечный момент времени, когда груз 3 переместился на расстояние s; T0 – начальная кинетическая энергия (T0 = 0);
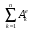– сумма работ внешних сил и моментов на заданном перемещении рассматриваемой системы.Конечная кинетическая энергия T равна сумме кинетических энергий вращательных движений дисков 1 и 2 и поступательного движения груза 3:
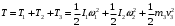, (2)где I1, I2 – осевые моменты инерции дисков 1 и 2; 1, 2 – их угловые скорости; v3 – скорость груза 3.
Выразим кинетическую энергию T через искомую скорость v3 (рисунок 2). Из рисунка 2 видно, что угловая скорость
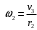, а ω2R2 = ω1r1.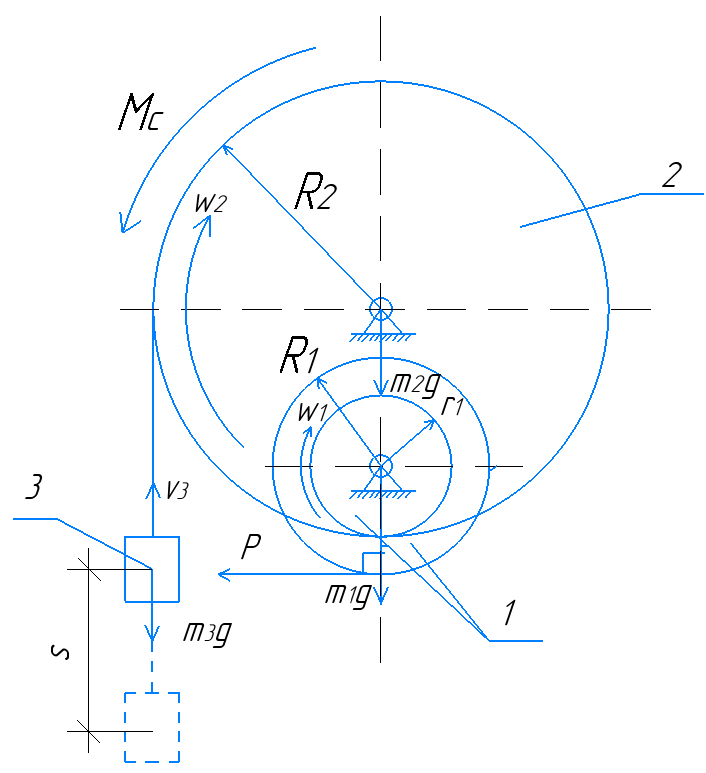
Рисунок 2 – Схема системы с расстановкой всех сил
Следовательно, угловая скорость диска 1 равна:
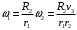
Моменты инерции дисков 1 и 2 равны соответственно:
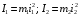
В результате подстановки этих формул в уравнение (2) получаем кинетическую энергию T в следующем виде:
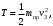(3)где
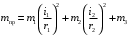– приведённая масса рассматриваемой системы.Сумма работ внешних сил и моментов, действующих на рассматриваемую механическую систему, равна:
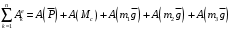(4)где
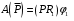– работа постоянной силы
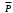, равная произведению её момента PR1 на угол поворота φ1 диска 1;
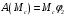– работа постоянного момента Mc
сил сопротивления;
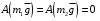– работы сил тяжести, действующих на диски 1 и 2; эти работы равны нулю, так как центры тяжести C1 и C2 этих дисков остаются постоянными;
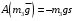– работа силы тяжести, действующей на груз 3, равная взятому со знаком «минус» произведению силы тяжести m3g на высоту подъёма s груза 3.Кроме вышеперечисленных сил и моментов на систему действуют также динамические реакции, приложенные в шарнирах C1 и C2. Работы этих реакций из-за неподвижности шарниров C1 и C2 равны нулю и на рисунке 2 они не показаны.
Выразим углы поворота φ1 и φ2 дисков 1 и 2 через путь s, пройденный грузом 3. Воспользуемся для этого равенствами
и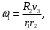 
в которых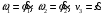 
Интегрируя эти равенства по времени с нулевыми начальными данными получаем:
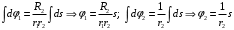
После подстановки этих выражений для φ1 и φ2 в уравнение (4) сумма работ внешних сил записывается в виде:
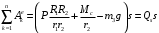(5)где
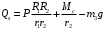– обобщённая сила, соответствующая координате s.С учётом полученных выражений для кинетической энергии (3) и суммы работ (5) формулу (1) для теоремы об изменении кинетической энергии получаем в следующем окончательном виде:
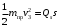.Отсюда получим, что скорость груза 3, начавшего движение из состояния покоя, после перемещения на расстояние s равна:
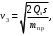(6)где приведённая масса системы:
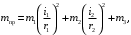(7)а обобщённая сила:
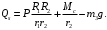(8)