МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Сибирский государственный университет науки и технологий

имени академика М.Ф. Решетнева»

Институт информатики и телекоммуникаций
Кафедра информационно-управляющих систем


Отчет по лабораторной работе №1
по дисциплине: «Вычислительная математика»
Тема: Численное решение систем линейных алгебраических уравнений

Вариант 10

Преподаватель Кириллов К. А.
Обучающийся БИЭ21-01, Пульмановский В. И.

Красноярск 2023 г.


a
Общее задание

Дана система линейных алгебраических уравнений (СЛАУ)

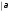
Au f 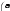, (1)

¹¹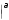

где _{A }²¹ 31

^a41


_a

a
12 13 a₂₂ a₂₃ a₃₂ a<sub>33

a42</sub> a<sub>43

14</sub>  ^u₁  ^f₁ 




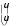
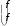
a

a
^{a24 }, _{u }^u2 _, _{f }^f2 _. 34  3  3 44 4 4

1. Решить СЛАУ (1) методом Гаусса с выбором главного элемента по

столбцам.

2. Привести СЛАУ (1) к виду

uBuF,

приемлемому для применения метода простой итерации, и проверить выполнение достаточного условия сходимости этого метода, т. е.

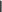
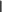B q1, (2)

<sup>1


</sup>
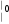
где BEA, F f , E ^0



^0

0 0 1 0 0 1

0 0

⁰



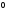
₀, значение выбрать таким, чтобы

¹

выполнялось неравенство (2).

Решить эту СЛАУ методом простой итерации

u_k1 Bu_kF
с точностью 0,01, предварительно преобразовав ее к виду, приемлемому

для применения этого метода. В качестве начального приближения выбрать

^u₀ ^{0, где 0 }^0,0,0,0T ^.
В качестве условия остановки итерационного процесса (для

достижения заданной точности ) использовать неравенство



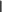
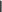
u_k1 u_k1q, (3)
где q– константа из неравенства (2). Имеет место неравенство

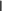
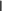
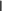
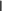
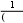^εk1q^{uk1 uk,}
где ε_ku_kU, U – вектор точного решения СЛАУ, u_k1 и u_k – векторы приближенного решения СЛАУ, полученные на k1-й и k-й итерациях соответственно. Следовательно, если выполняется неравенство

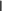
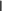
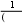1q^{uk1 uk,}
равносильное неравенству (3), то справедливо и неравенство

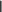
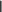ε_k,
обеспечивающее нахождение вектора u_k приближенного решения СЛАУ с

заданной точностью .

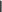
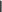В качестве нормы u_k1 u_k вектора u_k1 u_k взять октаэдрическую

норму, определяемую равенством


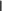
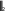
4
^{u }^ui^{, где u u}1^,u2^,u3^,u4 ^T ^, i1
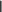
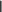а в качестве нормы B матрицы B – норму, согласованную с октаэдрической

нормой вектора, определяемую следующим образом:
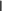
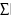
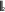
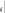
B max 4 b, где B b4 .

₁j4 _i1

Вариант22:

_5,401 u₁ 0,519u₂ 0,364u₃ 0,283u₄ 0,243, _0,295u₁ 4,830u₂ 0,421u₃ 0,278u₄ 0,231,

_0,524u₁ 0,397u₂ 4,723u₃ 0,389u₄ 0,721, _0,503u₁ 0,264u₂ 0,248u₃ 4,286u₄ 0,220.

Выполнение работы
1. СЛАУ методом Гаусса с выбором главного элемента по столбцам.
Алгоритм метода Гаусса. Пусть дана система уравнений:



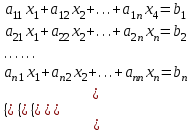
При решении методом Гаусса система приводится к ступенчатому виду:



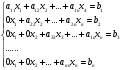
Для решения уравнения методом Гаусса необходимо знать, как выполняются элементарные преобразования систем линейных уравнений. Таких преобразований имеется четыре типа:

1. Умножение обеих частей уравнения на любое ненулевое число.

2. Перестановка уравнений системы местами.

3. Добавление (или вычитание) к обеим частям одного уравнения соответствующих частей другого уравнения, умноженного на любое ненулевое число.

4. Удаление нулевых строк.

Общие зависимости прямого хода для расширенной матрицы:

Ведущее уравнение не изменяется.

Для последующих уравнений 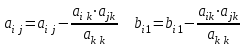, i = k + 1,…, n; j = k + 1,..., n.

Обратный ход начинается с вычисления последнего неизвестного системы линейных уравнений и заканчивается вычислением первого неизвестного. При обратном ходе используются только строки прямого хода.

Формулы обратного хода для полученной матрицы

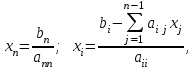
i = n – 1,…,1

При методе Гаусса с выбором главного элемента по столбцам производится сортировка по строкам, чтобы в ведущей строке диагональный элемент по модулю должен быть наибольшим среди ниже лежащих строк.

Текст программы Visual studio на С++:

#include

#include

using namespace std;
int main()

{

setlocale(LC_ALL, "Russian");

int n, i;

double a[10][10];

double b[10][10];

double x[10];

double aa, bb;

n = 4; //Задание матрицы А и вектора b (вектор b нах-ся в элементах А[1,5..4,5])

a[0][0] = 5.401; a[0][1] = 0.519; a[0][2] = 0.364; a[0][3] = 0.283; a[0][4] = 0.243;

a[1][0] = 0.295; a[1][1] = 4.830; a[1][2] = 0.421; a[1][3] = 0.278; a[1][4] = 0.231;

a[2][0] = 0.524; a[2][1] = 0.397; a[2][2] = 4.723; a[2][3] = 0.389; a[2][4] = 0.721;

a[3][0] = 0.503; a[3][1] = 0.264; a[3][2] = 0.248; a[3][3] = 4.286; a[3][4] = 0.220;

for (int j = 0; j < 4; j++)

for (int k = 0; k < 5; k++)

b[j][k] = a[j][k];

for (int k = 0; k < n; k++) //Поиск максимального элемента в первом столбце

{

aa = abs(a[k][k]);

i = k;

for (int m = k + 1; m < n; m++)

if (abs(a[m][k]) > aa)

{

i = m;

aa = abs(a[m][k]);

}

if (aa < 0.000001) //проверка на нулевой(близкий к нулевому) элемент

{

cout << endl;

cout << "Система не имеет решения" << endl;

}

if (i != k) //перестановка строк

for (int j = k; j < n + 1; j++)

{

bb = a[k][j];

a[k][j] = a[i][j];

a[i][j] = bb;

}

aa = a[k][k]; //преобразование k'й строки

a[k][k] = i;

for (int j = k + 1; j < n + 1; j++)

a[k][j] = a[k][j] / aa;

for (int il = k + 1; il < n; il++) //преобразование строк

{

bb = a[il][k];

a[il][k] = 0;

if (bb != 0)

for (int j = k + 1; j < n + 1; j++)

a[il][j] = a[il][j] - bb * a[k][j];

}

}

for (int il = n - 1; il >= 0; il--) //Нахождение решений СЛАУ

{

x[il] = 0;

aa = a[il][n];

for (int j = n - 1; j >= il + 1; j--)

aa = aa - a[il][j] * x[j];

x[il] = aa;

}

cout << "Исходная система:" << endl; //вывод матрицы b(исходной матрицы а)

for (int il = 0; il < n; il++)

{

for (int jl = 0; jl < n; jl++)

cout << b[il][jl] << " ";

cout << " | " << b[il][n] << endl;

}

cout << "Решение системы:" << endl; //вывод решений

for (int il = 0; il < n; il++)

cout << "x[" << il << "]=" << x[il] << endl;

}


Результат выполнения:



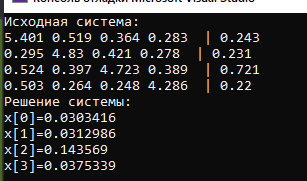
Получено решение методом Гаусса:

u=
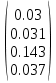
2. Находим решение СЛАУ методом итераций.

Алгоритм:

Пусть дана система линейных уравнений:



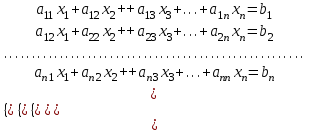
Приведем исходную систему к виду:



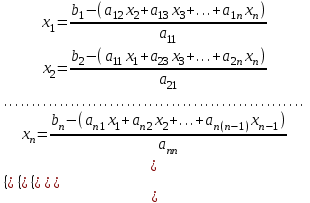
Сама итерационная формула имеет вид:



Решение методом итераций будет сходиться, если любая из норм матрицы будет меньше 1:

||||₁= 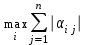< 1

||||₂= < 1

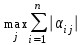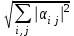||||₃= < 1.

Формула метода итераций:

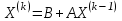
Вычисления завершаются в случае

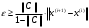
Где С – норма, которая использована для проверки сходимости.
Проверим выполнимость условия сходимости процесса итерации (преобладание диагональных элементов):

5,401 > 1,166=0,519+0,364+0,283;

4,830 > 0,994=0,295+0,421+0,278;

4,723 > 1,31=0,524+0,397+0,389;

4,286 > 1,015=0,503+0,264+0,248;
Условие сходимости процесса итерации выполняется.

Напишем интерполяционную формулу:


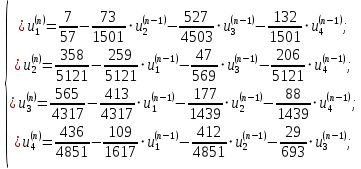
Вычислим норму матрицы (число ):





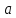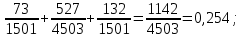
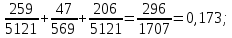
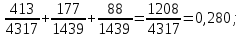
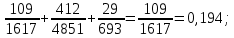
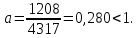
В качестве начального приближения положим .

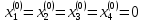Итерации продолжим до выполнения условия:



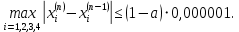
#include

#include

using namespace std;
int main()

{

setlocale(LC_ALL, "Russian");

double eps, q, x1, x2, x3, x4, y1, y2, y3, y4, s;

int i;

eps = 0.000001;

q = 3109.0 / 4317;

x1 = 0; x2 = 0; x3 = 0; x4 = 0;

s = 0.5; i = 0;

while (s > eps * q)

{

y1 = 7.0 / 57 - 73.0 * x2 / 1501 - 527.0 * x3 / 4503 - 132.0 * x4 / 1501;

y2 = 358.0 / 5121 - 259.0 * x1 / 5121 - 47.0 * x3 / 569 - 206.0 * x4 / 5121;

y3 = 565.0 / 4317 - 413.0 * x1 / 4317 - 177.0 * x2 / 1439 - 88.0 * x4 / 1439;

y4 = 436.0 / 4851 - 109.0 * x1 / 1617 - 412.0 * x2 / 4851 - 29.0 * x3 / 693;

i = i + 1;

s = abs(x1 - y1);

if (s < abs(x2 - y2))

s = abs(x2 - y2);

else if (s < abs(x3 - y3))

s = abs(x3 - y3);

else if (s < abs(x4 - y4))

s = abs(x4 - y4);

x1 = y1; x2 = y2; x3 = y3; x4 = y4;

}

cout << " x1=" << x1 << endl;

cout << " x2=" << x2 << endl;

cout << " x3=" << x3 << endl;

cout << " x4=" << x4 << endl;

cout << "Число итераций=" << i << endl;

}

Результат выполнения:




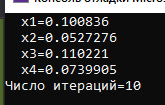
Таким образом, потребовалось 10 итераций.

Решение
u=

---

Смотрите также файлы

• .docx

• Программа среднего профессионального образования 44. 02. 02 Преподавание в начальных классах Дисциплина Теоретические основы начального курса математики с методикой преподавания Практическое занятие 2.pdf

• Ресей Денсаулы сатау министрлігіні gbou vpo orgma.docx

• Христианская семья.pptx

• 5 октября вышел Бегущий по лезвию 2049 Дени Вильнева, прямой сиквел первой части, снятой Ридли Скоттом в 1982 году. У нас между фильмами прошло 35 лет, в постапокалиптичном, киберпанкнеонуарном мире франшизы 30.rtf