МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Сибирский государственный университет науки и технологий

имени академика М.Ф. Решетнева»

Институт информатики и телекоммуникаций
Кафедра информационно-управляющих систем


Отчет по лабораторной работе №1
по дисциплине: «Вычислительная математика»
Тема: Численное решение систем линейных алгебраических уравнений

Вариант 3

Преподаватель Кириллов К. А.
Обучающийся БИЭ21-01, Бондарев В. А.

Красноярск 2023 г.


a
Общее задание

Дана система линейных алгебраических уравнений (СЛАУ)

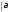
Au f 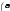, (1)

¹¹

где _{A }²¹ 31

^a41


_a

a
12 13 a₂₂ a₂₃ a₃₂ a<sub>33

a42</sub> a<sub>43

14</sub>  ^u₁  ^f₁ 




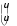
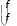
a

a
^{a24 }, _{u }^u2 _, _{f }^f2 _. 34  3  3 44 4 4

1. Решить СЛАУ (1) методом Гаусса с выбором главного элемента по

столбцам.

2. Привести СЛАУ (1) к виду

uBuF,

приемлемому для применения метода простой итерации, и проверить выполнение достаточного условия сходимости этого метода, т. е.

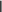B q1, (2)

<sup>1


</sup>
где BEA, F f , E ^0



^0

0 0 1 0 0 1

0 0

⁰



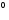
₀, значение выбрать таким, чтобы

¹

выполнялось неравенство (2).

Решить эту СЛАУ методом простой итерации

u_k1 Bu_kF
с точностью 0,01, предварительно преобразовав ее к виду, приемлемому

для применения этого метода. В качестве начального приближения выбрать

^u₀ ^{0, где 0 }^0,0,0,0T ^.
В качестве условия остановки итерационного процесса (для

достижения заданной точности ) использовать неравенство



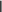
u_k1 u_k1q, (3)
где q– константа из неравенства (2). Имеет место неравенство

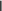
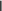
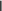
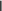
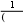^εk1q^{uk1 uk,}
где ε_ku_kU, U – вектор точного решения СЛАУ, u_k1 и u_k – векторы приближенного решения СЛАУ, полученные на k1-й и k-й итерациях соответственно. Следовательно, если выполняется неравенство

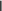
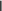
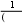1q^{uk1 uk,}
равносильное неравенству (3), то справедливо и неравенство

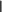
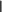ε_k,
обеспечивающее нахождение вектора u_k приближенного решения СЛАУ с

заданной точностью .

В качестве нормы u_k1 u_k вектора u_k1 u_k взять октаэдрическую

норму, определяемую равенством


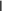
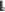
4
^{u }^ui^{, где u u}1^,u2^,u3^,u4 ^T ^, i1
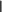
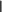а в качестве нормы B матрицы B – норму, согласованную с октаэдрической

нормой вектора, определяемую следующим образом:
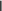
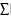
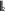
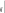
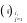B max 4 b, где B b4 .

₁j4 _i1

Вариант3:



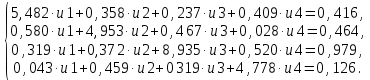
Выполнение работы
1. Решение СЛАУ методом Гаусса
Решение линейной системы методом Гаусса реализовано в функции SolveByGauss. Она принимает в качестве входных параметров матрицу коэффициентов и столбец свободных членов системы и пытается выполнить процедуру гауссова исключения в цикле по всем столбцам.

На каждом шаге в качестве главного элемента выбирается наибольший по модулю среди элементов ниже главной диагонали. Выбранный элемент сравнивается с заданным параметром ZeroCoef, взятым равным 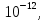чтобы предотвратить попытки деления на малые числа. В случае, если модуль главного элемента оказался меньше этой величины, матрица считается вырожденной, и функция SolveByGauss возвращает В противном случае функция завершается успешно, возвращает 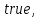а в выходной параметр 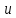записывается найденное решение системы.

На каждом шаге отображается результат исключения, а после успешного завершения – найденное решение системы.

Текст программы Visual studio на С++:
///////////////////////////////////////////////////////////////////////////////

// решение методом Гаусса

//

// A и f - матрица коэффициентов и столбец свободных членов системы

// u - вектор решения системы (выходной параметр)

//

// возвращаемое значение - true, если система успешно решена, и false,

// если на некотором шаге ведущий элемент

// оказался по модулю меньше порогового значения,

// установленного для проверки вырожденности

//

///////////////////////////////////////////////////////////////////////////////

bool SolveByGauss(const double A[N][N], const double f[N], double u[N])

{

double M[N][N];

double b[N];

int i;

int j;

int iPivotRow;

double dblSum;
for (i = 0; i < N; ++i)

{

for (j = 0; j < N; ++j)

M[i][j] = A[i][j];
b[i] = f[i];

}
for (i = 0; i < N - 1; ++i)

{

if (abs(M[i][i]) < ZeroCoef)

return false;
if (FindPivotElm(M, i, i, iPivotRow))

SwapRows(M, b, i, iPivotRow);
cout << endl

<< "Исключение с помощью коэффициента А("

<< i + 1 << "," << i + 1 << ")." << endl

<< endl;
EliminateCol(M, b, i, i);
cout << "Результат исключения:"

<< endl;
OutLinSys(M, b);

}
for (i = N - 1; i >= 0; --i)

{

dblSum = b[i];
for (j = i + 1; j < N; ++j)

dblSum -= M[i][j] * u[j];
u[i] = dblSum / M[i][i];

}
return true;

Результат работы этой части приложения показан на снимке экрана:


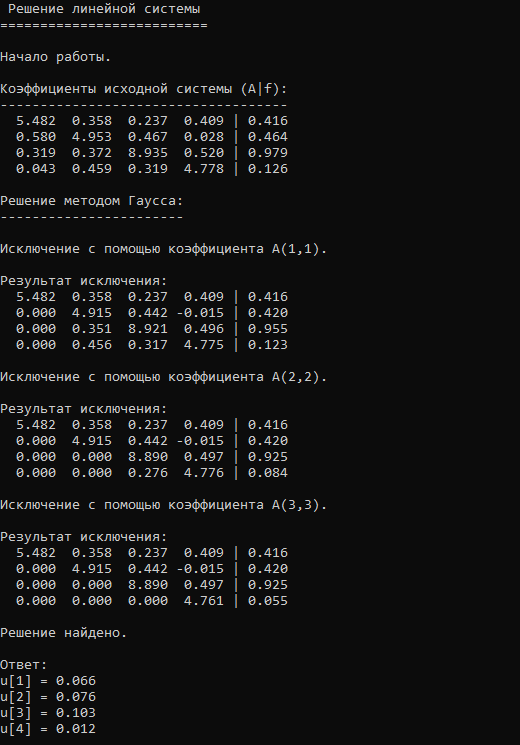
Получено решение методом Гаусса:

u=

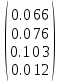
2. Решение методом простой итерации
Для применения метода простой итерации система преобразуется к заданному виду

Диагональные коэффициенты исходной матрицы принимают значения в промежутке от 4,778 до 8,935, т.е. от 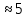до 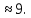Середина такого промежутка - 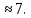В качестве параметра 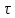взято значение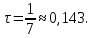

Преобразованная матрица 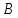оказывается имеющей норму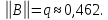

Это обеспечивает сходимость метода простой итерации.
Решение методом простой итерации для преобразованной системы реализовано в виде функции SolveBySimpleIters. Она принимает в качестве входных параметров коэффициенты и свободные члены системы, а также заданную точность 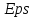и предельно допустимое число итераций MaxIters (для предотвращения зависания).

В случае успеха полученное решение заносится в выходной параметр 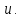Этот параметр также используется в качестве входного для задания начального приближения.

Погрешность на каждом шаге контролируется с помощью вычисления нормы разности двух векторов предыдущего и последующего приближений. Для этих вычислений используется функция VectorDiffNorm.

Текст программы Visual studio на С++:
///////////////////////////////////////////////////////////////////////////////

// решение методом простой итерации

//

// В и F - матрица коэффициентов и столбец свободных членов системы

// u - вектор решения системы (на входе - начальное приближение,

// на выходе - результат итераций)

// Eps - требуемая точность

// MaxIters - предельно допустимое число итераций

//

///////////////////////////////////////////////////////////////////////////////

bool SolveBySimpleIters(const double B[N][N], const double F[N],

double u[N],

const double Eps = 0.01, const int MaxIters = 1000)

{

int i;

int j;

double dblMinDiagElm = abs(B[0][0]);
for (i = 1; i < N; ++i)

if (dblMinDiagElm > abs(B[i][i]))

dblMinDiagElm = abs(B[i][i]);
assert(dblMinDiagElm > ZeroCoef);
double dblPrevU[N];

double dblNextU[N];
for (i = 0; i < N; ++i)

{

dblNextU[i] = u[i];

// обеспечивается заведомое нарушение

// условия сходимости

// на начальной итерации

dblPrevU[i] = dblNextU[i] + Eps + 1;

}
int iIterNo = 0;

double dblSum;

double q = MatrixNorm(B);

double Eps1q = Eps * (1 - q);
while ((iIterNo < MaxIters) && (VectorDiffNorm(dblPrevU, dblNextU) > Eps1q))

{

++iIterNo;
for (i = 0; i < N; ++i)

dblPrevU[i] = dblNextU[i];
for (i = 0; i < N; ++i)

{

dblSum = 0;
for (j = 0; j < N; ++j)

dblSum += B[i][j] * dblPrevU[j];
dblNextU[i] = dblSum + F[i];

}
//////////////////////////////////////////////////////////////////////////////

// debug

//////////////////////////////////////////////////////////////////////////////

cout << "Итерация " << iIterNo << ":" << endl;

cout << "-------------" << endl;

cout << endl;

for (int k = 0; k < N; ++k)

cout << " u[" << k + 1 << "] = " << fixed << setprecision(OutSolutionPrec)

<< dblNextU[k] << endl;
cout << endl;
cout << " || NextU - PrevU || = " << scientific << setprecision(1)

<< VectorDiffNorm(dblNextU, dblPrevU) << endl;
cout << endl;

}
for (i = 0; i < N; ++i)

u[i] = dblNextU[i];
return iIterNo < MaxIters;

}

Результат работы этой части приложения показан на снимках экрана:




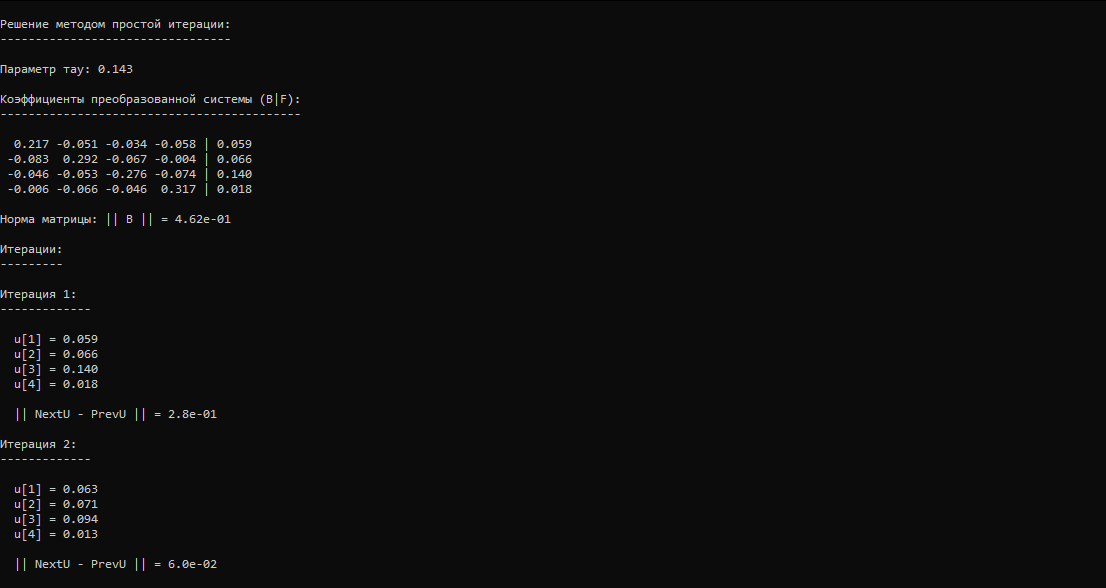
Таким образом, потребовалось 4 итерации.
Решение:
u=

---

Смотрите также файлы

• Отчет по лабораторной работе на тему.docx

• Б 9 Проектирование, строительство, реконструкция, капитальный ремонт объектов металлургической промышленности.doc

• Задачи 1.docx

• Астрент в арбитражном процессе Козлова Анна.pptx

• Контрольный диктант 8 по теме Имя прилагательное Цель.docx