Существует несколько разных способов определения передаточной функции по кривой разгона. Так, один из методов предполагает некоторые графические решения и применение диаграммы Ольденбурга-Сарториуса для определения постоянных времени. Другой метод предполагает анализ импульсной характеристики и единичного импульсного возмущения для определения динамических свойств объекта. Третий способ предполагает разложение инверсной передаточной функции в ряд Тейлора и определение ее коэффициентов.

Причем, учитывая неточность графических методов, очевидно, что передаточная функция будет описывать динамические свойства объекта не точно, а лишь приближенно. Поэтому имеет смысл определять ее всеми возможными способами, после чего оценить их адекватность экспериментальным данным, чтобы выбрать из имеющихся передаточных функций именно ту, которая отражает свойства объекта наиболее точно.

РАСЧЕТ ОДНОКОНТУРНОЙ СИСТЕМЫ РЕГУЛИРОВАНИЯ

Задание:

Динамические свойства объекта регулирования по каналу регулирующего воздействия определены импульсной характеристикой.

Регулируемая величина — температура перегретого пара котельного агрегата. Импульсная характеристика получена в результате нанесения возмущения, созданного скачкообразным уменьшением и последующим скачкообразным увеличением через τ_имп подачи конденсата на впрыск в пароохладитель на величину Ξ_вх.имп , измеренную в процентах хода регулирующего органа (% х.р.о.). Значения Ξ_вх.имп и τ_имп определены вариантом задания. Максимальный расход конденсата на впрыск, соответствующий 100% х.р.о., составляет 6 т/час. Номинальная температура перегретого пара 400^оС. Изменение регулируемой величины (в отклонениях от номинального значения) в результате импульсного возмущающего воздействия, задано в безразмерном виде таблицей 1.

Исходные данные:

t	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
	0	0	0	1	2	5	10	12	14	15	14	12	10	6	3	1	0

---

ПИД-регулятор

τ_имп= 60 секунд

Ξ_{вх. имп} = 25 % х.р.о.

a_t = 25 секунд

a_θ = 2,0 градуса

М = 1,62

1. 
   Перейдем к размерному виду импульсной характеристики.
   

Изменение регулируемой величины задано таблицей в безразмерном виде. Чтобы перейти к размерному виду, нужно умножить значение безразмерного времени и безразмерного отклонения на соответствующие значения масштабных коэффициентов a_t и a_θ:

t = t*a_t

θ = *a_θ

Тогда зависимость θ(t) примет следующий вид:

t	0	25	50	75	100	125	150	175	200	225	250	275	300	325	350	375	400
θ	0	0	0	2	4	10	20	24	28	30	28	24	20	12	6	2	0

Построим график импульсной характеристики θ(t):

2. 
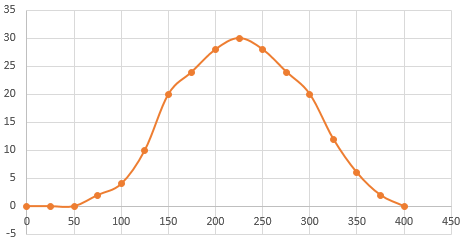
   Построим кривую разгона.
   

Для перестройки импульсной характеристики в кривую разгона необходимо разбить наблюдаемое время на интервалы величиной t_имп., найти интерполяцию импульсной характеристики в точках t_i и сложить ординаты графиков θ(t) и h(t) по формуле:

h(t_i) = h(t_i-1) + θ(t_i)

Тогда полученная зависимость h(t) будет выглядеть следующим образом:

t	0	60	120	180	240	300	360
θ	0	0,7	8,3	24,7	29,2	20	4,2
h	0	0,7	9	33,7	62,9	82,9	87,1

---

Построив график этой зависимости, получим кривую разгона:

3. 
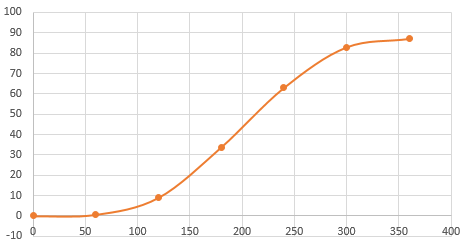
   Определим передаточную функцию по импульсной характеристике
   

Определим динамические параметры объекта по импульсной характеристике:



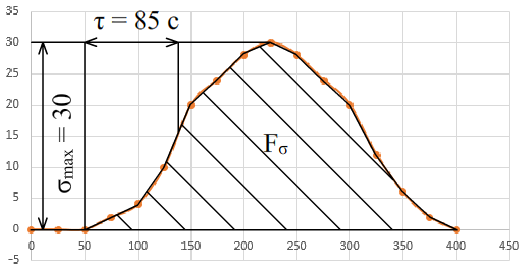
F_σ = Σ_i=1¹⁶ _i*a_t = 5250 – площадь графика изменения регулируемой величины.

σ_max = 30 – максимальное отклонение регулируемой величины.

τ = 135 – 50 = 85 – время запаздывания.

Импульсный входной сигнал:



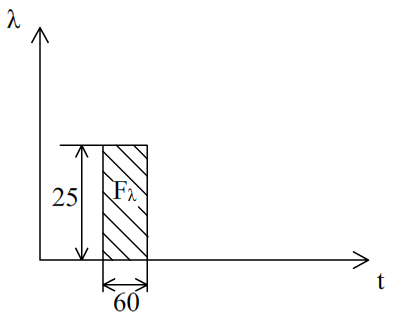
F_λ = Ξ_вх.имп*­τ_имп. = 25*60 = 1500 – площадь графика импульсного возмущения.

k = F_σ/F_λ = 5250/1500 = 3,5 – коэффициент усиления.

T_a = F_λ/σ_max = 1500/30 = 50 – постоянная времени.

Передаточная функция будет иметь вид:

W(P) = k*e^-tp/(T_a*P + 1)

W(P) = 3,5*e^-85p/(50*P + 1)

4. 
   Определим передаточную функцию методом Ольденбурга-Сарториуса
   

Коэффициент усиления найдем как отношение установившегося значения выхода к значению входа:

k = 87,1/25 = 3,5

Время запаздывания определим путем графического решения уравнения:

h(τ) = Δ = (0,02÷0,05)*h(t)_max, откуда

τ = 100 c при Δ = 4,355^o

Параметры T_a и T_c определим графически, найдя точку перегиба графика переходной функции:



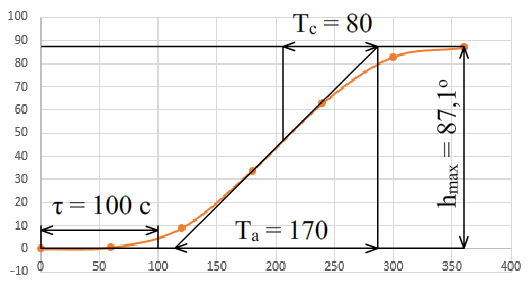
T_a = 170

T_c = 80

T_c/T_a = 0.48

Округляем T_c/T_a до 0,73 и по известному отношению T_c/T_a с помощью диаграммы Ольденбурга-Сарториуса определяем постоянные времени T₁ и T₂:



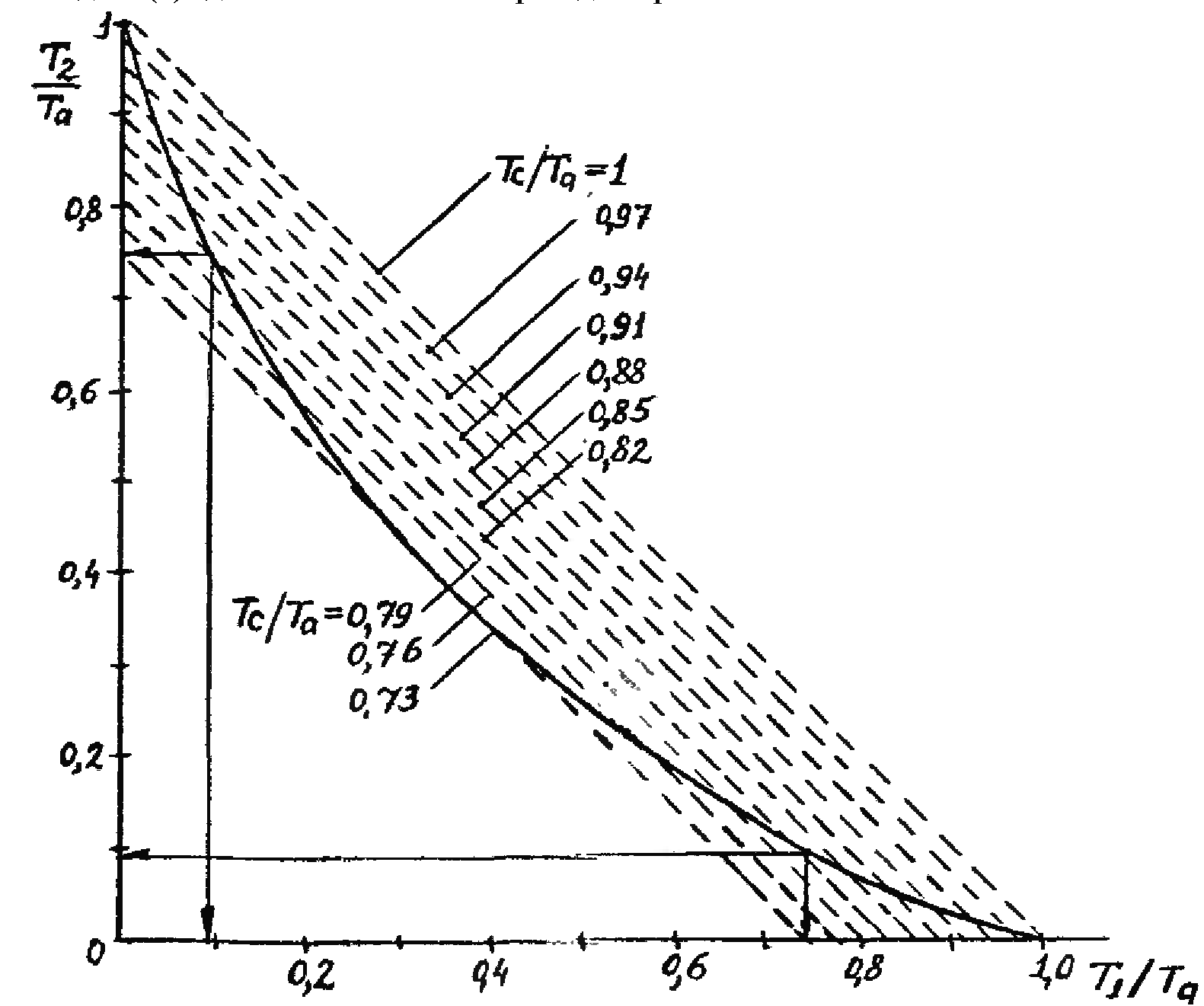
T₁ / T_a = 0.4

T₂ / T_a = 0.4

Т₁ = 0,4*T_a = 68

Т₂ = 0,4*T_a = 68

Передаточная функция будет иметь вид:

---

W(P) = k*e^-tp/((T₁*P + 1)*(T₂*P + 1))

W(P) = 3,5*e^-100p/((68*P + 1)*(68*P + 1))

W(P) = 3,5*e^-100p/(4624*P² + 136*P + 1)

5. 
   Определим передаточную функцию методом площадей при помощи программы simou.exe
   

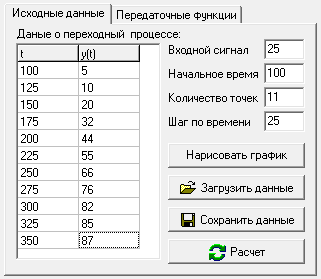
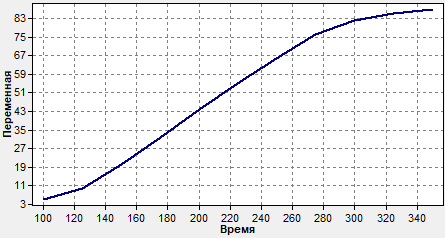
Получили семейство из девяти передаточных функций, из которых в дальнейшем будем рассматривать следующую:

W(P) = 3,484/(3326,7*P² + 101,7*P + 1)

Переходная кривая для этой функции выглядит следующим образом:

6. 
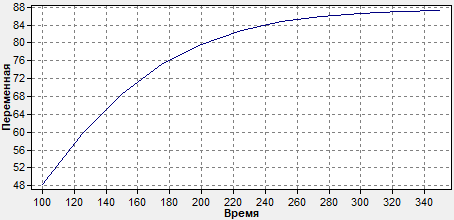
   Построим и сравним переходные характеристики передаточных функций с помощью пакета Simulink
   

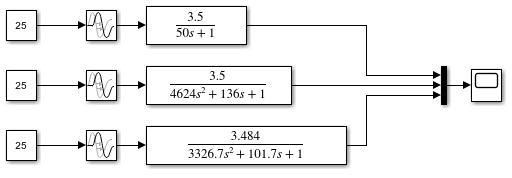
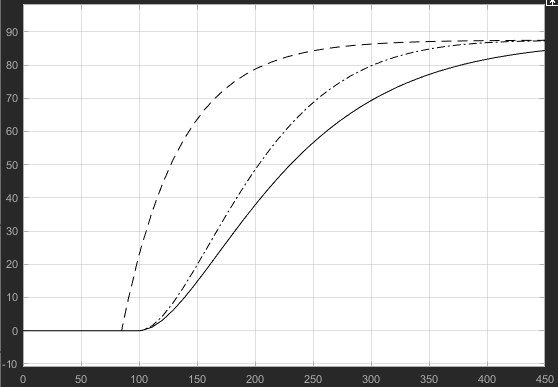
На изображении выше изображены графики:

Пунктирной линией – передаточной функции, полученной по импульсной характеристике.

Сплошной линией – передаточной функции, полученной методом Ольденбурга-Сарториуса.

Штрихпунктирной линией – передаточной функции, полученной методом площадей.

7. 
   Оценим дисперсию полученных переходных характеристик передаточных функций
   

Графически определим отклонения всех трех переходных кривых от экспериментальных данных по формуле:

σ_i² = (h_эксп.i – h_расч.i)², где

σ_расч.i² – дисперсия в точке t_i

h_эксп.i – экспериментальное значение величины h(t)

h_расч.i – расчетное значение величины h(t)

i	1	2	3	4	5	6	7
ti	0	60	120	180	240	300	360
σимп.i2	0	0,5	1225	1624	445,2	9,6	0
σолд.i2	0	0,49	36	32,5	98	193,2	82,8
σсим.i2	0	0,49	25	18,49	4,41	8,41	4,41

---

Теперь, зная дисперсии всех трех кривых h(t) во всех точках t_i, можем найти их общие дисперсии, как среднее арифметическое от всех найденных ранее по формуле:

σ² = (1/n)Σ_i=1ⁿ (σ_расч.i²)

Тогда

σ_имп² = 472

σ_олд² = 63,3

σ_сим² = 8,74

Как видно, меньше всего от экспериментальных значений величины h(t) отклоняется кривая, передаточная функция которой была найдена методом Симою. Тогда в дальнейшем будем рассматривать именно ее.

8. 
   Построим частотные характеристики объекта регулирования (АФХ, АЧХ и ФЧХ)
   

АФХ - амплитудно-фазовая характеристика



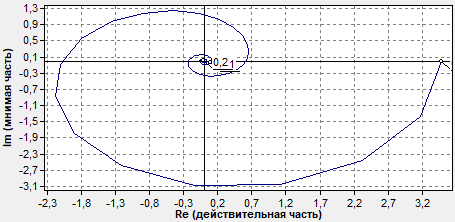
АЧХ – амплитудно-частотная характеристика



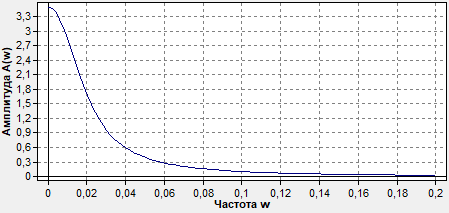
ФЧХ – фазово-частотная характеристика

9. 
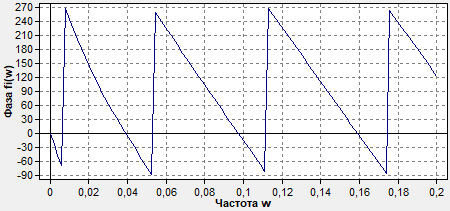
   Рассчитаем оптимальные значения параметров настройки
   

Определим значение показателя колебательности, решив уравнение:

M = (1 + m²)/2*m

2*m*M = 1 + m2

m² – 2*m*M + 1 = 0

M = 1,62

m₁ = 2,8945

m₂ = 0,3455

Из двух корней m₁ и m₂ выбираем меньший, т.е. принимаем m = 0,3455.

Перейдем к инверсной расширенной частотной характеристике, произведя подстановку P = ω*(j - m) и преобразовав передаточную функцию к следующему виду:

W(m, ij)_инв. = 1/W(m, ij)

W(m, ij) = (4624*P² + 136*P + 1)/3,5

Выделив из нее действительную и мнимую части, сможем определить значения параметров настройки C₁ и C_0, при С₂ = 0.5:



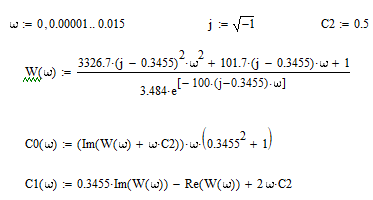
Построим график зависимости C₀(C₁) и определяем из него C₁ и C₀ следующим образом: находим на кривой точку максимума и выбираем точку правее него. Полученные значения C₁ и C₀ подставим в схему системы управления и сравним их между собой по значению интегрально-квадратичного критерия качества.

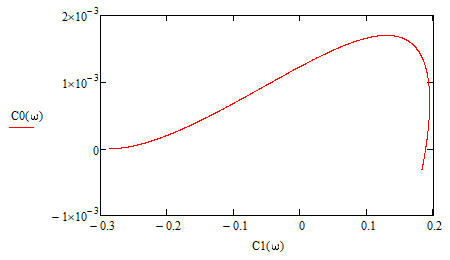
Значение параметра настройки C1	Значение параметра настройки C0	Интегральный критерий качества I
0,15447	0,00165	89450
0,16447	0,00160	86650
0,17029	0,00155	84960
0,17463	0,00150	83660
0,17839	0,00145	82520
0,18091	0,00140	81670

---

Смотрите также файлы

• Лекция Понятия, сущность и функции коммерческого отдела.docx

• Цифровая экономика и Информационные системы в экономике Синергия 8097% Что не свойственно процессу цифровизации.pdf

• Достижения советской исторической науки История вкп(б). Краткий курс была опубликована в.docx

• Учебник. М. Норма инфрам, 2018. С. 60. 12 2 Система органов исполнительной власти 12.docx

• Задание 4.doc