Параметры настройки C₀ и C₁ при С₂ = 1,0

Значение параметра настройки C1	Значение параметра настройки C0	Интегральный критерий качества I
0,16565	0,00165	86710
0,17483	0,00160	84250
0,18114	0,00155	82540
0,18571	0,00150	81260
0,18935	0,00145	80200
0,19236	0,00140	79300

Параметры настройки C₀ и C₁ при С₂ = 1,5

Значение параметра настройки C1	Значение параметра настройки C0	Интегральный критерий качества I
0,17457	0,00165	84640
0,18496	0,00160	82030
0,19159	0,00155	80330
0,19622	0,00150	79100
0,20063	0,00145	77940
0,20382	0,00140	77050

Как видно из таблиц, наилучшими свойствами будет обладать регулятор с настройками: C₀ = 0,00140 C₁ = 0,20382 при С₂ = 1,5.

10. 
    Построим схему полученной системы регулирования
    

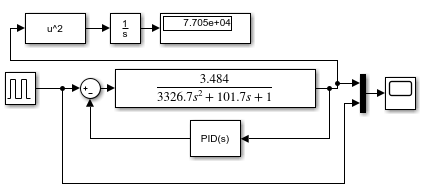
График переходного процесса полученной системы регулирования:

11. 
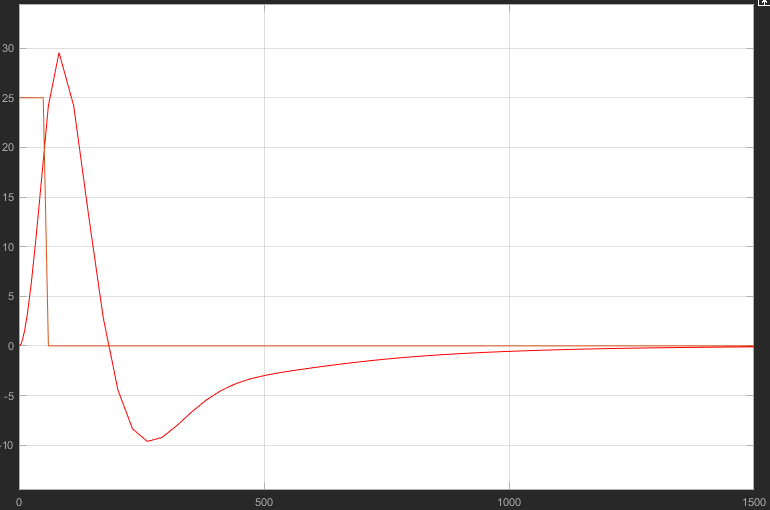
    Получим передаточную функцию замкнутой системы относительно возмущающего воздействия, найдем и построим КЧХ замкнутой системы относительно возмущающего воздействия.
    

Передаточная функция объекта регулирования:

---

W(P)_об = 3,484/(3326,7*P² + 101,7*P + 1)

Передаточная функция ПИД-регулятора:

W(P)_рег = 0,20382 + 0,00140/p + 1.5*p

Передаточная функция внешнего возмущающего воздействия:

W(P)_возм = 3,5/(50*P + 1)

Передаточная функция замкнутой системы относительно внешнего возмущающего воздействия:

W(P) = (W(P)_об*W(P)_возм)/(1 + W(P)_об*W(P)_рег)

W(P) =

Произведем замену p = ω*j:



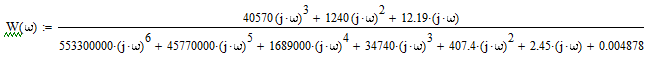
Построим КЧХ замкнутой системы, относительно возмущающего воздействия:



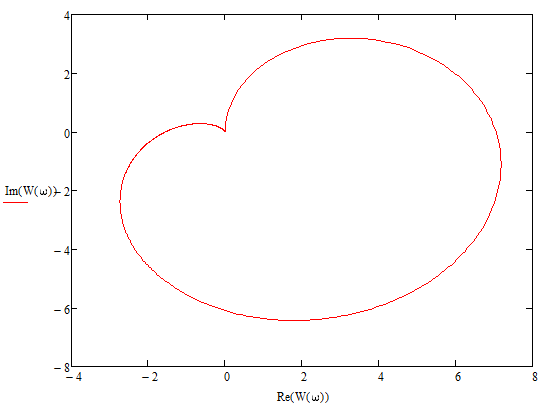
12. Построим схему полученной системы регулирования и оценим качество переходного процесса по регулированию.

Схема системы регулирования, график переходного процесса:





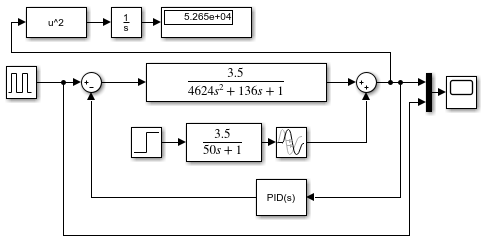
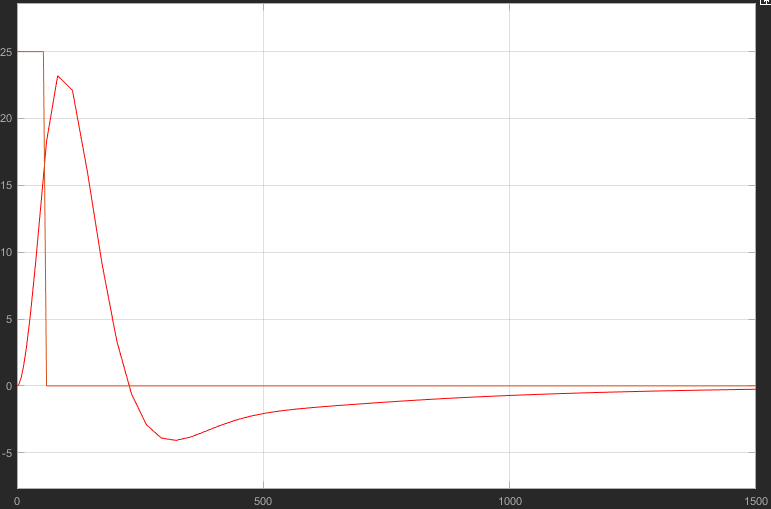
Оценим качество переходного процесса по возмущению:

I = 5265 – квадратичный интегральный критерий качества

h_max1 = 30 – амплитуда 1 колебания

h_max2 = 8 – амплитуда 2 колебания

t_п = 1000 с – время переходного процесса

t_max1 = 82 с – время достижения первого экстремума

t_max2 = 260 с – время достижения второго экстремума

ω = 2π/T = 2*3,14/(260 – 82) = 0,0353 – частота переходного процесса

ξ = (y_max2 – y_уст)/(y_max1 – y_уст) = 0,2642 – время затухания за 1 период

ψ = (y_max1 - y_max3)/y_max1– степень затухания мы рассчитать не можем, т.к. 3-е колебание не достигается

m = -ln(1 - ψ)/2π– степень колебательности мы рассчитать не можем, т.к. она зависит от степени затухания

ВЫВОД

В данном курсовом проекте я:

1. Построил кривую разгона по импульсной характеристике и тремя разными способами определил ее передаточную функцию, выбрав из них наиболее подходящую.

2. Построил частотные характеристики объекта регулирования: АФХ, АЧХ и ФЧХ.

3. Для ПИД-регулятора определил оптимальные значения параметров настройки, обеспечивающие минимальное значение интегрального квадратичного критерия качества.

---

4. Рассчитал и построил КЧХ замкнутой системы относительно внешнего возмущающего воздействия.

5. Смоделировал переходной процесс в системе регулирования при внешнем возмущающем воздействии.

Построенная система АСР, взятая на основе реального объекта управления устойчива, так как в ней возможен установившийся режим, вследствие чего регулируемая величина, температура перегретого пара, будет поддерживаться на необходимом уровне.

СПИСОК ЛИТЕРАТУРЫ

1. 
   Прохватилов В.В., Кантемиров В.И. Методические указания к выполнению курсового проекта по теории автоматического управления: Методические указания / Прохватилов В.В.,
   

Кантемиров В.И.– Астрахань: Изд-во АГТУ, 2007.– 35 с.

2. 
   Стефани Е.П. Основы расчета настройки регуляторов теплоэнергетических процессов / Стефани Е.П.– М: Энергия, 1972.– 376 с.
   

---

Смотрите также файлы

• Лекция Понятия, сущность и функции коммерческого отдела.docx

• Цифровая экономика и Информационные системы в экономике Синергия 8097% Что не свойственно процессу цифровизации.pdf

• Достижения советской исторической науки История вкп(б). Краткий курс была опубликована в.docx

• Учебник. М. Норма инфрам, 2018. С. 60. 12 2 Система органов исполнительной власти 12.docx

• Задание 4.doc