Файл: Вариант вычислить. Найдите скалярное произведение полей и, заданных в различных системах координат. Результат представьте в системе координат, указанной в задании..docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 46
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
| ВАРИАНТ 1 1. 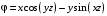 . Вычислить . Вычислить 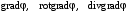 . .2. Найдите скалярное произведение полей 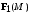 и и 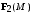 , заданных в различных системах координат. Результат представьте в системе координат, указанной в задании. , заданных в различных системах координат. Результат представьте в системе координат, указанной в задании.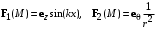 (сферические). (сферические).3. Плоскость z = 0 равномерно заряжена с поверхностной плотностью электрического заряда 0,1 нКл/м2. Определите поля Е и D во всем пространстве, считая, что заряды находятся в вакууме. |
| ВАРИАНТ 2 1. 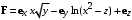 . Вычислить . Вычислить 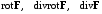 . .2. Найдите скалярное произведение полей 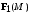 и и 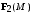 , заданных в различных системах координат. Результат представьте в системе координат, указанной в задании. , заданных в различных системах координат. Результат представьте в системе координат, указанной в задании.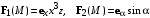 (декартовы). (декартовы).3. Разность потенциалов между пластинами плоского воздушного конденсатора равна 1 В. Определите плотность поверхностного заряда на обкладках, считая, что эффектами искажения поля около края пластин можно пренебречь. Расстояние между обкладками 5 мм. |
| ВАРИАНТ 3 1. 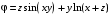 . Вычислить . Вычислить 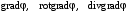 . .2. Найдите скалярное произведение полей 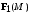 и и 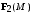 , заданных в различных системах координат. Результат представьте в системе координат, указанной в задании. , заданных в различных системах координат. Результат представьте в системе координат, указанной в задании.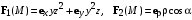 (декартовы). (декартовы).3. Между пластинами плоского конденсатора находится двухслойный диэлектрик. Толщина слоев d1 = 2 мм, d2 = 5 мм; относительные диэлектрические проницаемости слоев ε1 = 2, ε2 = 3. Площадь пластин 25 см2, расстояние между ними d = d1 + d2. На верхней пластине равномерно распределен заряд qA = 10–9 Кл, на нижней пластине – заряд qB = –qA. Определите напряженность электрического поля в конденсаторе и разность потенциалов между пластинами. Считайте, что эффектами искажения поля около края пластин можно пренебречь. |
| ВАРИАНТ 4 1. 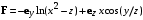 . Вычислить . Вычислить 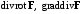 2. Найдите скалярное произведение полей 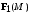 и и 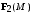 , заданных в различных системах координат. Результат представьте в системе координат, указанной в задании. , заданных в различных системах координат. Результат представьте в системе координат, указанной в задании.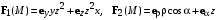 (цилиндрические). (цилиндрические).3. На поверхности металлического шара радиусом 10 см равномерно распределен электрический заряд. Шар окружен воздухом. Определите поверхностную плотность заряда, если на расстоянии 20 см от центра шара напряженность электрического поля составляет 50 В/м. |
| ВАРИАНТ 5 1. 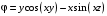 . Вычислить . Вычислить 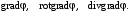 2. Найдите скалярное произведение полей 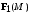 и и 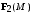 , заданных в различных системах координат. Результат представьте в системе координат, указанной в задании. , заданных в различных системах координат. Результат представьте в системе координат, указанной в задании.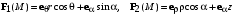 (цилиндрические). (цилиндрические).3. Бесконечно протяженный круговой цилиндр радиуса  с диэлектрической проницаемостью с диэлектрической проницаемостью  , находящийся в среде с диэлектрической проницаемостью , находящийся в среде с диэлектрической проницаемостью 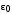 , заряжен статическим электричеством. Пользуясь формулой Гаусса, найдите вектор электрического поля на расстоянии ρ от оси цилиндра. Заряд равномерно распределен по поверхности цилиндра с плотностью , заряжен статическим электричеством. Пользуясь формулой Гаусса, найдите вектор электрического поля на расстоянии ρ от оси цилиндра. Заряд равномерно распределен по поверхности цилиндра с плотностью  . . |
| ВАРИАНТ 6 1. 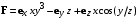 . Вычислить . Вычислить 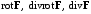 . .2. Найдите скалярное произведение полей 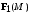 и и 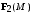 , заданных в различных системах координат. Результат представьте в системе координат, указанной в задании. , заданных в различных системах координат. Результат представьте в системе координат, указанной в задании.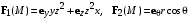 (сферические). (сферические).3. Бесконечно протяженный плоский слой толщиной d равномерно заряжен с объемной плотностью ρ0. Абсолютные диэлектрические проницаемости среды, находящейся внутри и вне слоя, одинаковы и равны ε0. Определите напряженность электрического поля во всем пространстве. Считайте, что слой расположен в области –d/2 < z < d/2. |
| ВАРИАНТ 7 1. 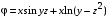 . Вычислить . Вычислить 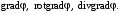 2. Найдите векторное произведение полей 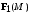 и и 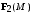 , заданных в различных системах координат. Результат представьте в системе координат, указанной в задании. , заданных в различных системах координат. Результат представьте в системе координат, указанной в задании.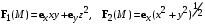 (декартовы). (декартовы).3. Внутри бесконечно длинной цилиндрической области радиусом r0 равномерно распределен электрический заряд с объемной плотностью ρ0. Абсолютные диэлектрические проницаемости внутренней и внешней областей равны εа1 и εа2 соответственно. Определите напряженность электрического поля во всем пространстве. |
| ВАРИАНТ 8 1. 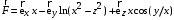 . Вычислить . Вычислить 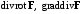 2. Найдите векторное произведение полей 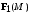 и и 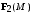 , заданных в различных системах координат. Результат представьте в системе координат, указанной в задании. , заданных в различных системах координат. Результат представьте в системе координат, указанной в задании.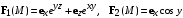 (декартовы). (декартовы).3. Сферический конденсатор образован двумя концентрическими металлическими сферами с радиусами а и b (а < b). Между сферами находится диэлектрик с относительной диэлектрической проницаемостью ε. Получите выражение для емкости данного конденсатора. |
| ВАРИАНТ 9 1. 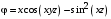 . Вычислить . Вычислить 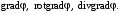 2. Найдите векторное произведение полей 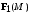 и и 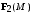 , заданных в различных системах координат. Результат представьте в системе координат, указанной в задании. , заданных в различных системах координат. Результат представьте в системе координат, указанной в задании.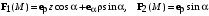 (цилиндрическая). (цилиндрическая).3. Внутри сферической области радиусом а равномерно распределен электрический заряд с объемной плотностью ρ0. Абсолютные диэлектрические проницаемости области и окружающей среды одинаковы и равны ε0. Определите напряженность электрического поля во всем пространстве |