МЕКТЕП МАТЕМАТИКА КУРСЫНДА МАТЕМАТИКАЛЫҚ ЕСЕПТЕРДІ ГЕОМЕТРИЯЛЫҚ ТӘСІЛДЕРМЕН ШЕШУ ӘДІСТЕМЕСІНІҢ ҚОЛДАНЫСЫ

Семей қаласының Шәкәрім атындағы мемлекеттік университетінің жаратылыстану математика факультетінің 5В010900 - Математика мамандығының 4 курс студенті Тайжігітова Мадина Серікболқызы.

Математика курсының материалдарын оқытуда математикалық есептерді шешудің әртүрлі тәсілдері қарастырылады. Оқушыларды шығармашылыққа баулитын, математикалық білімді саналы түрде игеруге мүмкіндік беретін тәсілдер көбірек маңызға ие болуда.

Шығармашылық ойлау қабілетінің және оқу материалын формальды емес игерудің бірден бір көрсеткіші ақпараттың берілуін геометриялық түрде қолдана білу болып табылады. Осы қолданысты білу, әсіресе, алгебралық (мәтіндік) есептерді шешуде маңызды орын алады, өйткені ол қиял мен ойлау қабілетін ұштастыруға мүмкіндік береді.

Есептерді геометриялық тәсілмен шешу әдісі Евклид заманында (б. э. д III ғ) пайда болған және тек қана геометрияда емес алгебрада да қолданылған. Оның алгебрадағы қолданысының бір ерекшелігі – Евклид есептердің шешімін геометриялық салулар мен геометрия заңдарының көмегімен пайымдаған. Осылайша геометриялық алгебра дамыды [1]. Біз алгебралық есептерді геометриялық тәсілдермен шығаруда геометриялық сызбалардың, геометрия заңдылықтарының, аналитикалық тәсіл элементтерінің (теңдеулер, арифметикалық өрнектер т.б) қолданыстарын үйренеміз. Мәтіндік есеп шартының геометриялық берілуін осы есептің геометриялық моделі деп атаймыз.

Алгебра курсында мәтіндік есептердің геометриялық моделінің 4 негізгі түрін қолдануға болады: а) бірөлшемді (сызықтық) диаграммалар; б) екіөлшемді диаграммалар; в) графикалық үлгілер; г) тапсырмада берілген фигуралардың сызбасы (геометриялық мазмұнды есептерде).

Біз мақаламызда бірөлшемді және екіөлшемді диаграммалар арқылы шешу жолдарын қарастырамыз.

Есепті геометриялық тәсілмен шығару 3 кезең арқылы жүзеге асады: 1) есептің геометриялық моделін кұру, яғни оны геометриялық тілге келтіру; 2) пайда болған геометриялық есептің шешімі; 3) нәтижесін геометриялықтан табиғиға айналдыру.

Осы кезеңдердің орындалуын алгебралық есептерді алғашқы 3 түрдің геометриялық моделіне сүйене отырып шешуде толығырақ қарастырамыз.

Сызықтық диаграмма мен кесінді ұзындығы қасиетінің қолданылуы.

Сызықтық диаграмма – ұзындығы қарастырылып отырған шаманың сандық мәніне сәйкес келетін бір немесе бірнеше кесінді. Алгебра курсында сызықтық диаграммамен шешілетін есептер екі түрде беріледі: 1) дәл сол уақытта бір ғана оқиға суреттеледі; 2) екі оқиға берілген: бастапқы және соңғы.

---

Бірінші түрдегі есепті шешуде сызықтық диаграмма статистикалық модель ретінде қолданылады, яғни орындау барысында өзгермей иллюстративті қызмет атқарады. Екінші түрдегі есептер сызықтық диаграмманы көбірек қажет етеді. Бұл есептерді осы тәсілмен шешу барысы екі түрлі : алдымен бастапқы (соңғы) объект қимылын білдіретін диаграмма, ал содан кейін есеп шарты бойынша қайтадан соңғы (бастапқы) жағдай орындалатындай өзгереді. Мысал келтірейік.

1- есеп: Көкөніс қоймасының біреуінде екіншісіне қарағанда 3 есе артық картоп бар. Бірінші қоймадан 450 т картоп алынып, ал екіншіге 120 т картоп қосқанда екі қоймадағы картоптар салмағы тең болды. Бастапқыда әр қоймада қанша тонна картоп болды?

I. Есепті оқығаннан кейін оқушылар мынадай сұрақтарға жауап беруі тиісті:

1) Есепте қанша оқиға қарастырылады? (Екі: бастапқы және соңғы)

2)Диаграмманы қай оқиғадан бастап салу керек? ( Бастапқы оқиғадан бастап соңғы оқиғаға көшу немесе соңғы оқиғаға байланысты диаграмма құрып бастапқыға көшуге болады. Бірінші нұсқаны қарастырамыз).

3). Бастапқы оқиға диаграммасы қалай салынады? (Біреуі екіншісінен 3 есе үлкен болатындай екі кесінді салынады.)

Оқушылар осы шарттар бойынша диаграмма салып, есепті әрі қарай талқылайды.


4) Бастапқы оқиға мен соңғы оқиғаны қалай бейнелеуге болады?

(Бірінші кесіндіден 450 т –ны бейнелейтін кесіндіні алып, екінші бөлігіне 120 т –ны бейнелейтін кесінді қосамыз.)

5) Бөліктер кез келген түрде алына ма? (Жоқ, нәтижесінде екі қоймада да картоптар салмағы тең болғандықтан, қайта қосылған кесінділер тең болу керек.)

Осы айтылғандарды орындағаннан кейін соңғы оқиғаға байланысты диаграмма құрылады.

II. Салынған сызықтық диаграмма шешімі кесінді ұзындығының қасиетіне негізделетін алгебралық есепті геометриялық түрге келтіреді. Шешімін жүйе құрмай-ақ, диаграммадан қарап та білуге болады.

III. Алдымен диаграммада берілгендерді жазып алу керек. Содан кейін сызбада кейбір мәндер белгілі көрініп тұрғандықтан бірте-бірте қысқаша түрге көше береміз.

1- тәсіл

I. AB кесіндісі бірінші қоймадағы картоптар мөлшері(1-сурет), CD екінші қоймадағы картоп мөлшері. АВ = 3CD қоймадағы картоптар айырмашылығы.

BK бірінші қоймадан алынған, ал DE екінші қоймаға әкелінген картоп мөлшері. АК = CE қоймада қалған картоптар мөлшері.

II. BM = 2AM, DE =

---

MK (салу бойынша).

⁴⁵⁰




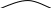
А

В




М

К

F

120







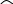
C D E


MB = MK = KB = 120+450 = 570. AM = 570:2 = 285. CD = AM=285, AB = 3CD = 3˟285 = 855.

III. Жауабы: Бірінші қоймада 855 т картоп болды, екіншіде 285 т .

2- тәсіл.

АК = CE = x болсын, онда: х+450 = 3(x-120), бұда н х = 405, бұдан CD = 405 – 120 = 285. AB = 855.

3 – тәсіл.

CD = BF = FM = x болсын, BM = 2x, онда BM – MK = 450, бұдан x = 285. Яғни, CD = 285, AB = 855.

4 – тәсіл.

CD = x болсын, онда AB = 3x. AK = CE болғандықтан x + 120 = 3x - 450

x = 285.

II. Екіөлшемді диаграммалар мен ауданның қасиетін қолдану.

Қарастырылып отырған өлшем басқа екі өлшемнің көбейтіндісі ретінде келтірілетін тапсырмаларды тіктөртбұрыштың ауданы (параллелограмм, үшбұрыш), яғни екіөлшемді диаграммалар көмегімен шешуге болады. Екіөлшемді диаграмма бір немесе бірнеше тіктөртбұрыштар ауданынан құралуы мүмкін.

Жаңа тәсілді үйрету кезінде бірмезетте есеп шешудің екі тәсілі де: теңдеу арқылы (сызбасыз) және екіөлшемді диаграмма арқылы шешу де қарастырылады. Бұл – оқушыларға екі тәсілді де салыстыра отырып меңгеруге қажетті. 7 сыныпта геометриялық тәсілдің мотивациялық кезеңінде қолдануға болатын мысал келтірейік.

Егер ескеретін болсақ бөлшек-рационал теңдеулермен оқушылар 8 сыныпта танысады. Екіөлшемді диаграмма бұл есепті сызықтық теңдеу арқылы шешуге мүмкіндік береді.

I. Алгебралық тәсілмен шешкенде мынадай теңдеу шығады.

x – катердің тұнық судағы жылдамдығы

Катердің өзен ағысымен жүзген жолы S = 4*(x+1,5)

Катердің өзен ағысына қарсы жүзген жолы S = 2*(x-1,5)

Есеп шарт бойынша: 4*(x+1,5) = 2*(x-1,5)*2,4

х = 16,5

II. MNOP үшбұрышының MN қабырғасы катердің өзен ағысымен жүргендегі жылдамдығы. MP катердің осы жылдамдықпен жүзіп өткен уақыт аралығын білдіреді. Егер х деп катердің тұнық судағы жылдамдығын белгілесек , онда MN = x + 1,5 (км/сағ). MP = 4(сағ).





P O

---

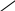
Өзен ағысымен

S₁



L

Q




4




2

Өзен ағысына қарсы

S₂









M x +1,5 N F x – 1,5 K

MNOP тіктөртбұрышының ауданы қайықтың өзен ағысымен жүзгендегі арақашықтығына тең: S₁ = MN*MP

NK = x – 1,5 – катердің өзен ағысына қарсы жүзгендегі жылдамдығы (км/сағ) онда KL катердің өзен ағысына қарсы жүзген уақыты. KL = 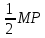= 2

NKLQ тіктөртбұрышының ауданы катердің өзен ағысына қарсы жүзгендегі жолын білдіреді. S₂ = NK* KL

S₁ = 2,4 S₂

(x+1,5)*4 = 2,4*( x -1,5)*2

4x+6=4,8x – 7,2

- 0,8x = - 13,2

x = 16,5

Қорыта келе геометриялық әдіс дегеніміз – ол оқушыларға жақсы идея ұсынатын әдіс. Бұл жерде оқушылар геометриялық заңдар мен геометриялық фигуралардың қасиеттерін пайдалана отырып, есеп шығарудың жеңіл және қызық екенін айқындайды. Сонымен біз кейбір алгебралық есептерді геометриялық әдіспен шығарып мынадай тұжырымға келдік.

---

Есептерді геометриялық жолмен шығаудың артықшылықтары:

• 
  есепті бұл жолмен шығару бастапқы іс – әрекетті нақты айқындайды;
  
• 
  графиктік сурет - теңдеулерді құрастыруда, есептердің бірнеше шығару жолдарын қарастырғанда талдау жасауды жеңілдетеді;
  
• 
  графиктерді қолдану аймағын кеңейтеді және оқушылардың графикті салу мәдениетін қалыптастырады;
  
• 
  теңдеулерді шешудің жаңа технологиясын көрсетеді;
  
• 
  пәндер ішіндегі (алгебра мен геометрия) байланыс және пәнаралық (математика және физика) байланысты көрсетеді.
  

Біз әр түрлі есептерді қарастыра отырып, оқушыларға бірнеше геометриялық әдістерді көрсетіп, есептерді шешуде алгебралық әдіс пен геометриялық әдісті салыстырдық; жеңіл және көрнекті геометриялық әдіс пен тригонометриялық есептер шығады. Бұл әдіс есептің дұрыс шығарылу сапасын тексереді; бұл жерде геометриялық әдіс оқушылардың ойлау қабілетін арттырады және уақытты үнемдей білуге үйретеді. Көбінесе жоғары сынып оқушыларына пайдалануға ыңғайлы.
Қолданылған әдебиеттер
1. Шыныбеков Ә.Н Ш - 97 Алгебра: Жалпы білім беретін мектептің 7 сыныбына арналған оқулық. – Алматы: Атамұра, 2003. – 176 бет. - 57 бет 242 есеп

2. Лунина Л. С – Мектептегі математика: Ғылыми – теориялық әдістемелік журнал. – Чехов қ, : Школа – Пресс, 1996. – 4 басылым – ОАлгебралық есептерді геометриялық тәсілдермен шығаруды үйрету .

3. В. А Далингер - Мектептегі математика: Ғылыми – теориялық әдістемелік журнал. – Чехов қ, : Школа – Пресс, 1996. – 4 басылым – Геометрияның алгебраға ықпалы.

---

Смотрите также файлы

• Вопрос 1 Назовите представителей социалдарвинизма в социологии 2 половины xixнач xx в.docx

• Дневник самоконтроля студента группы ург 1902 Савриева Фирдавса Дневник самоконтроля.docx

• Задания суммативного оценивания за 2 четверть по русскому языку 9 класс.docx

• Аи в макСиНаЛЬнО в асстомние дДолуовае т.docx

• Формы и методы воспитательной работы в творческом коллективе.docx