Файл: Методическое пособие к практическим занятиям по дисциплине Электротехника и электроника Автор составитель Погодин Д. В.doc

федеральное государственное бюджетное образовательное учреждение высшего образования
«Казанский национальный исследовательский технический
университет им. А.Н. Туполева-КАИ»

(КНИТУ-КАИ)

__________________________________________________________________________

Институт радиоэлектроники, фотоники и цифровых технологий
Кафедра радиоэлектроники и информационно-измерительной техники

Эквивалентные преобразования электрических цепей

-2 часа

Методическое пособие к практическим занятиям

по дисциплине Электротехника и электроника

Авторсоставитель: Погодин Д.В.

Казань - 2022г

https://youtu.be/_gNSKu1b2QY

ТЕМА Эквивалентные преобразования электрических цепей

Одним из простых методов расчета цепей является метод эквивалентных преобразований электрических схем. Согласно этому методу исходная схема преобразуется в схему, содержащую меньшее количество элементов, т.е. более простую, но эквивалентную исходной.

Цепи считаются эквивалентными, если их внешние электрические характеристики (u = f(i)) являются одинаковыми (подобными).

Существует пять основных способов соединения электрических элементов:

• 
  1.последовательное соединение
  
• 
  2. параллельное соединение
  
• 
  3. соединение элементов звездой
  
• 
  4. соединение элементов треугольником
  
• 
  5. смешанное соединение элементов
  

1. Последовательное соединение элементов

П
ри последовательном соединении элементов через них протекает один и тот же ток I₁ (рис. 1.1).

с ловием эквивалентности этих цепей являются равенства:

I₁ = I_ЭКВ; U = U_ЭКВ, R_ЭКВ= R₁ + R₂.

Следовательно, при последовательном соединении n сопротивлений эквивалентное сопротивление R_ЭКВ равно сумме этих сопротивлений

---

.

Е
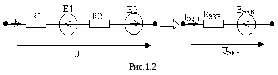
сли в ветви содержатся источники ЭДС, соединенные последовательно (рис. 12), то ЭДС источников складываются алгебраически: E_ЭКВ = E₁ – E₂. Положительное направление ЭДС эквивалентного источника берется произвольно. При этом со знаком «плюс» в формуле пишутся ЭДС тех источников, направления которых совпадут с направлением эквивалентного источника.

Т аким образом, можно сформулировать правила преобразования при последовательном соединении элементов:

п ри последовательном соединении элементов складываются их сопротивления, а ЭДС источников складываются алгебраически (с учетом знака).

Эквивалентное сопротивление при последовательном соединении всегда больше наибольшего сопротивления: R_ЭКВ > R₁, R_ЭКВ > R_2.

2. Параллельное соединение элементов

При параллельном соединении элементы находятся при одном и том же напряжении U. Пример параллельного соединения элементов представлен на рис. 1.3.

В
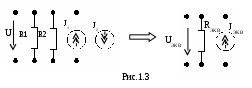
расчетах при параллельном соединении удобнее пользоваться понятием «проводимость», а не «сопротивление». Проводимость элемента обратно-пропорциональна его сопротивлению .

Правила преобразования при параллельном соединении элементов:

п ри параллельном соединении пассивных элементов кладываются их проводимости, а токи источников складываются алгебраически (с учетом знака).

Следовательно,

По приведенному примеру видно, что если параллельно включены источники тока (рис. 1.3), то их можно преобразовать в эквивалентный источник J_экв, ток которого равен алгебраической сумме токов источников, соединенных параллельно:

---

J_экв = J₁ - J₂. Положительное направление тока эквивалентного источника берется произвольно. При этом со знаком «плюс» в формуле пишутся токи тех источников, направления которых совпадут с направлением эквивалентного источника.

Полезно запомнить формулу соединения двух сопротивлений:

.

При параллельном соединении элементов эквивалентное сопротивление меньше наименьшего. При равенстве двух сопротивлений результат равен половине.

3. Эквивалентное преобразование источников электрических сигналов

Л 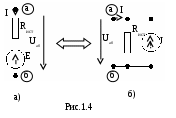юбой источник электрического сигнала может быть представлен одной из двух эквивалентных схем.

Схему 1 можно заменить схемой 2, если параметры схемы 2 выбраны из условий: I = E/R_i1, R_i2 = R_i1.

Схему 2 можно заменить схемой 1, если параметры схемы 1 выбраны из условий: E =IR_i1, R_i1 = R_i2.

Если источник ЭДС подключен к узлу, где сходится несколько ветвей, то возможно «расщепление» источника ЭДС (рис. 2.21, б). При этом, режим в цепи не изменится – всегда можно, соединив накоротко выводы всех источников, заменить их одним (показано пунктиром).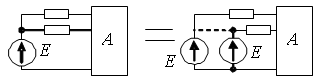

Рис.2.21б. Эквивалентный перенос источников ЭДС в смежные ветви

Источники тока тоже «расщепляют» (рис. 3.13), параллельно каждому сопротивлению. При этом режим в цепи не нарушается. Получившиеся источники токов с параллельно включенными проводимостями можно преобразовывать в эквивалентные источники ЭДС (рис.3.13).



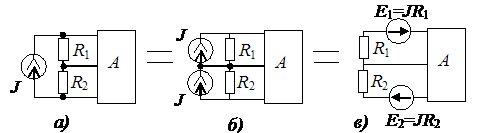
Рис. 3.13. Преобразование схем с источниками тока: а– исходная; б– преобразованная; в–с источником ЭДС

4. Эквивалентные преобразования при смешанное соединение элементов

Смешанным соединением называют сочетание последовательного и параллельного соединений резисторов.

При смешанном соединении элементов для эквивалентного преобразования пользуются

---

методом последовательных эквивалентных преобразований, т.е. последовательно преобразуются участки цепи, имеющие простое (только последовательное, или только параллельное) соединение элементов.

Поясним это на конкретном примере расчета электрической цепи (рис.1.3). Пример 1



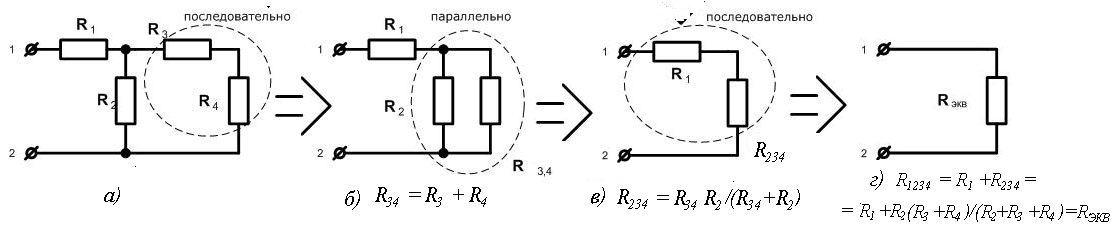
Пример 2.

Н
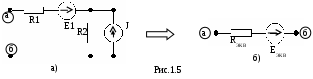
а рис. 1.5,а схема цепи со смешанным соединением элементов может быть преобразована в простую эквивалентную схему из двух элементов –(R_ЭКВ – E_ЭКВ) (рис. 1.5 б). Для этого сначала параллельный участок цепи (R₂ – J) преобразовать в последовательную схему – (R₂ – E₂). Получится участок цепи с последовательным соединением элементов (см. рис.1.6), который, как показывалось ранее, преобразуется в эквивалентную схему (см. рис. 1.5 б):

R _экв = R₁ + R₂; E₂ = J/R₂;

E_экв = E₁ – E₂ = E₁ – J/R₂.

5. Расчет неразветвленной цепи

В 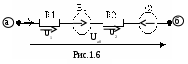неразветвленной ветви (см. рис. 1.6), содержащей различные резисторы и источники ЭДС, ток I₁ можно определить по формуле обобщенного закона Ома

,

где V_а, V_б – потенциалы точек а и б; U_аб =V_а –V_б – разность потенциалов или напряжение между точками а и б; ∑R – арифметическая сумма сопротивлений резисторов ветви; ∑E – алгебраическая сумма ЭДС источников. Со знаком “плюс” берут те ЭДС, направления которых совпадают с выбранным положительным направлением тока, а со знаком “минус” – ЭДС с противоположными направлениями.

В ветви, изображенной на рис. 1.6, ток определяется формулой:

.

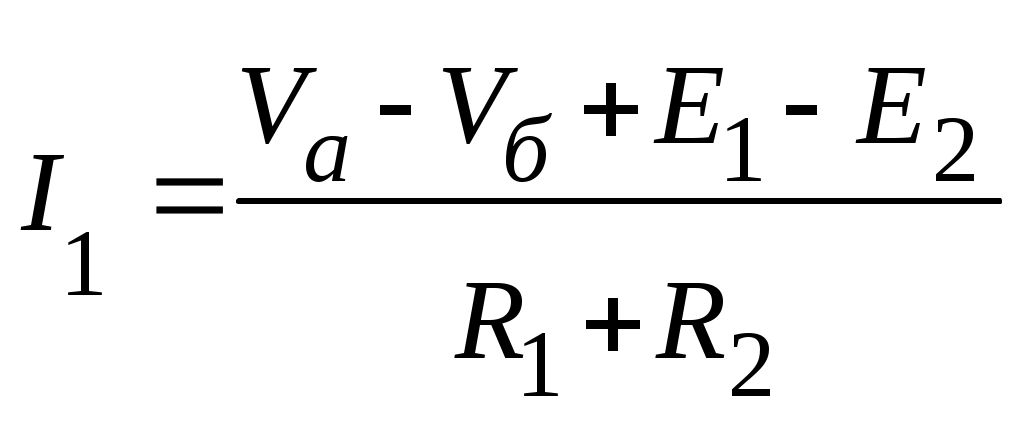6. Эквивалентные преобразования сложных схем

Если схема цепи, содержит большое число ветвей и различных источников, то такую схему можно преобразовать в простую эквивалентную путем преобразования отдельных участков схемы и уменьшения числа элементов. Это можно проиллюстрировать на примере.

---

Пример 1.1. Преобразовать схему цепи, изображенную на рис. 1.7 а, в эквивалентную (R_экв – E_экв) (рис. 1.7 б).

Решение. Задача решается в насколько этапов.

Следует начать преобразование не со стороны узлов а) и б), а с другой стороны схемы (справа).

С
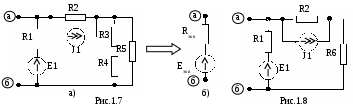
опротивления R₃ и R₄ соединены последовательно, а к ним параллельно подключено R₅. Этот участок преобразуется в одно сопротивление R₆:



Теперь образовался участок смешанной цепи из элементов (R₂ - J₁ - R₆) (см. рис.1.8). Его нужно преобразовать в последовательную цепь – (R₇ – E₂ ) (см. рис.1.9 а), где R₇ = R₂ + R₆, E₂ = J₁·R₂.

П
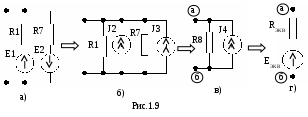
олученную схему нужно преобразовать в параллельные схемы (рис. 1.9 б, в).

Параметры преобразованных элементов определяются по формулам:

J₂ = E₁/R₁, J₃ = E₂/R₇, , J₄ = J₂ + J₃.

По условию задачи исходную схему (рис. 1.7 а) следует преобразовать в последовательную R_экв – E_экв (рис. 1.7 б или рис. 1.9 г).

Т аким образом,

R_ЭКВ = R₈; E_ЭКВ = J₄∙R₈.

Преобразование соединений треугольника и звезда

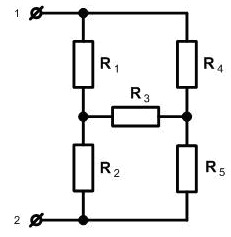
Иногда встречаются такие соединения нескольких элементов электрической цепи, в которых нет возможности выделить последовательное или параллельное соединение. Например схемы мостовой цепи изображен на рисунке ниже.

В таких случаях необходимо выполнить преобразование элементов соединенных по схеме звезда или треугольник. Это преобразование само по себе не является упрощением схемы (количество элементов цепи не меняется), однако приводит схему к виду в котором уже можно выделить последовательные или параллельные соединения элементов, а следовательно, упростить последующими преобразованиями.

---