Файл: Контрольная работа по дисциплине Теория информации, данные, знания Вариант 1. Выполнил(а) студент(ка) заочной формы обучения группы 21из замятина К. А.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 11.01.2024
Просмотров: 28
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Министерство образования науки и молодежной политики
Нижегородской области
Государственное бюджетное образовательное учреждение
высшего образования
«Нижегородский государственный инженерно-экономический университет» (ГБОУ ВО НГИЭУ)
Кафедра «Информационные системы и технологии»
Институт информационных технологий и систем связи
КОНТРОЛЬНАЯ РАБОТА
по дисциплине: «Теория информации, данные, знания»
Вариант №1.
Выполнил(а) студент(ка) заочной формы обучения группы 21-ИЗ Замятина К.А.
Проверил(а): к.ф.-м.н., доцент кафедры «Информационные системы и технологии» Астахова Т.Н.
г. Княгинино
2023 г.
Теоретическая часть:
Вопрос №I. Аналоговая и дискретная информация. Дискретизация информации
1. Дискретная информация характеризуется последовательными точными дискретными значениями некоторой величины. Аналоговая – непрерывным процессом (сигналом) изменения некоторой величины и может быть изменена в течение времени в соответствии с некоторыми физическими воздействиями. Непрерывные аналоговые сигналы, изменяются во времени или в пространстве от точки к точке.
2. Дискретизация – это преобразование непрерывного сигнала в дискретный формат, то есть представление этого сигнала по какому-либо конечномерному базису. Это представление состоит в проектировании сигнала на данный базис. Наиболее удобным с точки зрения организации обработки и естественным способом дискретизации является представление сигналов в виде выборки их значений (отсчетов) в отдельных, регулярно расположенных точках. Такой способ называют растрированием, а последовательность узлов, в которых берутся отсчеты – растром. Интервал, через который берутся значения непрерывного сигнала называется шагом дискретизации. Обратная шагу величина называется частотой дискретизации.
Вопрос №II. Семантическая мера информации
1. Семантическая мера информации — подход, при котором информация (сообщение) рассматривается с точки зрения своего содержания, смысла и существенности.
2. Среди семантических мер наиболее распространены содержательность, логическое количество, целесообразность и существенность информации:
Содержательность события определяется как отношение количества информации в сообщении к объёма сообщения и выражается через функцию меры
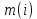 содержательности отрицания события. Оценка содержательности основана на математической логике, в которой логические функции истинности
содержательности отрицания события. Оценка содержательности основана на математической логике, в которой логические функции истинности 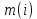 и ложности имеют формальное сходство с функциями вероятностей события
и ложности имеют формальное сходство с функциями вероятностей события 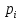 и антисобытия
и антисобытия 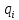 в теории вероятностей. Как и вероятность, содержательность события изменяется в пределах от 0 до 1.
в теории вероятностей. Как и вероятность, содержательность события изменяется в пределах от 0 до 1.Практическая часть:
I. Рассмотреть 3 распределения вероятностей символов алфавита: равномерное, P1(A) и P2(A). Для каждого распределения получить кодовые слова c использованием заданного алгоритма, вычислить среднюю длину кодового слова, избыточность и проверить неравенство Крафта.
| 2 | 0,4 | 0 |
| 20 | 0,1 | 1100 |
| 200 | 0,1 | 1101 |
| 0 | 0,5 | 1110 |
| 00 | 0,5 | 1111 |
| “_” | 0,3 | 110 |
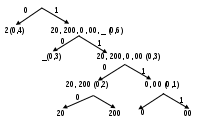
Таблица Вероятности символов и их кодовые слова
Вычисление кодовых слов символов
Вычислим количество информации воспользовавшись формулой Шеннона:
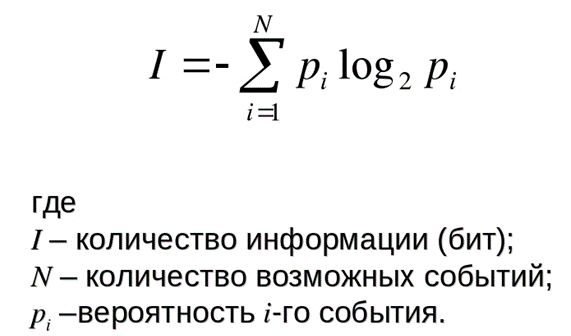
для вычисления избыточности кодирования
I = -0,4 * log2(0,4) - 0,01 * log2(0,01) - 0,1 * log2(0,1) - 0,05 * log2(0,05) - 0,05 * log2(0,05) - 0,3 * log2(0,3) = -0,4 * (-1,32) - 0,1 * (-3,32) - 0,1 * (-3,32) - 0,05 * (-4,32) - 0,05 * (-4,32) - 0,3 * (-1,74) = 0,528 + 0,332 + 0,332 + 0,216 + 0,216 + 0,519 = 2.146 бит.
Теперь необходимо вычислить среднюю длину кодового слова по формуле:

Формула вычисления средней длины кодового слова.
С = 0.4 + 0.01 * 4 + 0.1 * 4 + 0.05 * 4 + 0.05 * 4 + 0.3 * 3 = 2.5 бит
Вычислим избыточность кодирования по формуле R = C – I.
R = 2.5 – 2.146 = 0.354 бит
0 <= 0.354 < 1.
Проверим неравенство Крафта.
2^(-1) + 2^(-4) + 2^(-4) + 2^(-4) + 2^(-4) + 2^(-3) = 0.5 + 0.0625 +0.0625 + 0.0625 + 0.0625 + 0.125 = 0.875
Неравенство Крафта выполняется 0.875 <= 1.
Ответ:
Кодовые слова представлены в таблице “Вычисление кодовых слов символов”
Средняя длина кодового слова (C) = 2.5 бит.
Избыточность (R) = 0.354 бит.
Неравенство Крафта выполняется 0.875 <= 1.
II. Закодировать сообщение «LKJDD» при помощи арифметического кодирования.
Рассматриваем кодирование на отрезке [0;1], тогда вероятности появления каждого из символов в алфавите A = {L, K, J, D}
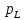 =0.2
=0.2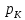 =0.2
=0.2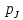 =0.2
=0.2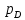 =0.4
=0.4Теперь с помощью отрезков начинаем кодирование:





Ответ:
Ответом является число имеющее наименьшее количество символов и находящееся в последнем отрезке алгоритма: 0,063