ВУЗ: Новосибирский государственный технический университет
Категория: Решение задач
Дисциплина: Информатика
Добавлен: 13.02.2019
Просмотров: 479
Скачиваний: 7
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Новосибирский государственный технический университет»
Факультет Автоматики и Вычислительной Техники
Кафедра Автоматизированных Систем Управления
РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА
по дисциплине «Методы анализа данных»
на тему «Классификация с помощью нейронной сети в пакетах STATISTICA и Deductor»
Выполнил студент группы АВТ-412:
Лазаревич М.М.
Проверил доцент кафедры АСУ:
Ганелина Н.Д.
Новосибирск
1 Цель работы
Для выбранного массива данных решить задачу классификации при использовании нейронной сети в пакетах STATISTICA и Deductor. Исследовать влияние параметров сети на качество решения в каждом из пакетов. Сравнить полученные результаты.
2 Постановка задачи
Необходимо построить нейронную сеть для классификации машин по значениям, основанным на множестве снимков моделей с разных ракурсов.
3 Исходные данные
Используемый массив содержит данные о силуэтах четырёх моделей машин. Данные основаны на снимках автомобилей с различных ракурсов. Все изображения были сняты с разрешением 128x128 пикселей в монохромном режиме в 6-х битном представлении. Изображения были использованы для получения бинарных силуэтов машин и отфильтрованы для удаления шума. Для каждой машины, за исключением машин класса “van” было сделано четрые набора по 60 изображений, покрывающих полный поворот вокруг оси.
Классы: opel, saab, bus, van
Количество экземпляров: 946
Количество пропущенных значений: 0
Количество экземпляров каждого класса:
opel 240
saab 240
bus 240
van 226
Количество атрибутов: 19
Атрибуты:
Compactness –
Компактность –
Circularity - Округлость
–
Distance circularity – Расстояние
округлости –
Radius ratio – Соотношение радиусов
–
Pr.axis aspect
ratio – Соотношение сторон
по главной оси –
Max.length aspect
ratio – Соотношение
максимальных длин –
Scatter ratio –
Коэффициент рассеяния –
Elongatedness – Вытянутость
–
Pr.axis
rectangularity – Прямоугольность
по главной оси –
Max.length
rectangularity – Прямоугольность
по максимальной длине –
Scaled variance along major axis – Масштабированная дисперсия вдоль главной оси
Scaled variance along minor axis – Масштабированная дисперсия вдоль минорной оси
Scaled radius of gyration – Масштабированный радиус вращения
Skewness about major axis – Асимметрия вдоль главной оси
Skewness about minor axis – Асимметрия вдоль минорной оси
Kurtosis about major axis – Эксцесс вдоль главной оси
Kurtosis about minor axis – Эксцесс вдоль главной оси
Hollows ratio –
Коэффициент пустот –
Class – Класс
Все значения неклассовых атрибутов являются целыми числами.
Описательные статистики представлены на рисунке 1. По ним видно, что ни один параметр выборки не близок к нормальному.
Рис 1. Описательные статистики значений атрибутов исследуемого массива данных
На рисунке 2 представлено распределение наблюдений по классам, оно примерно равномерное.
Рис 2. Распределение наблюдений по классам
На рисунке 3 представлена корреляционная матрица. Как видно по матрице, в ней довольно много пар с коэффициентом корреляции больше 0.7 по абсолютному значению, на основе этого принято решение о проведении факторного анализа.
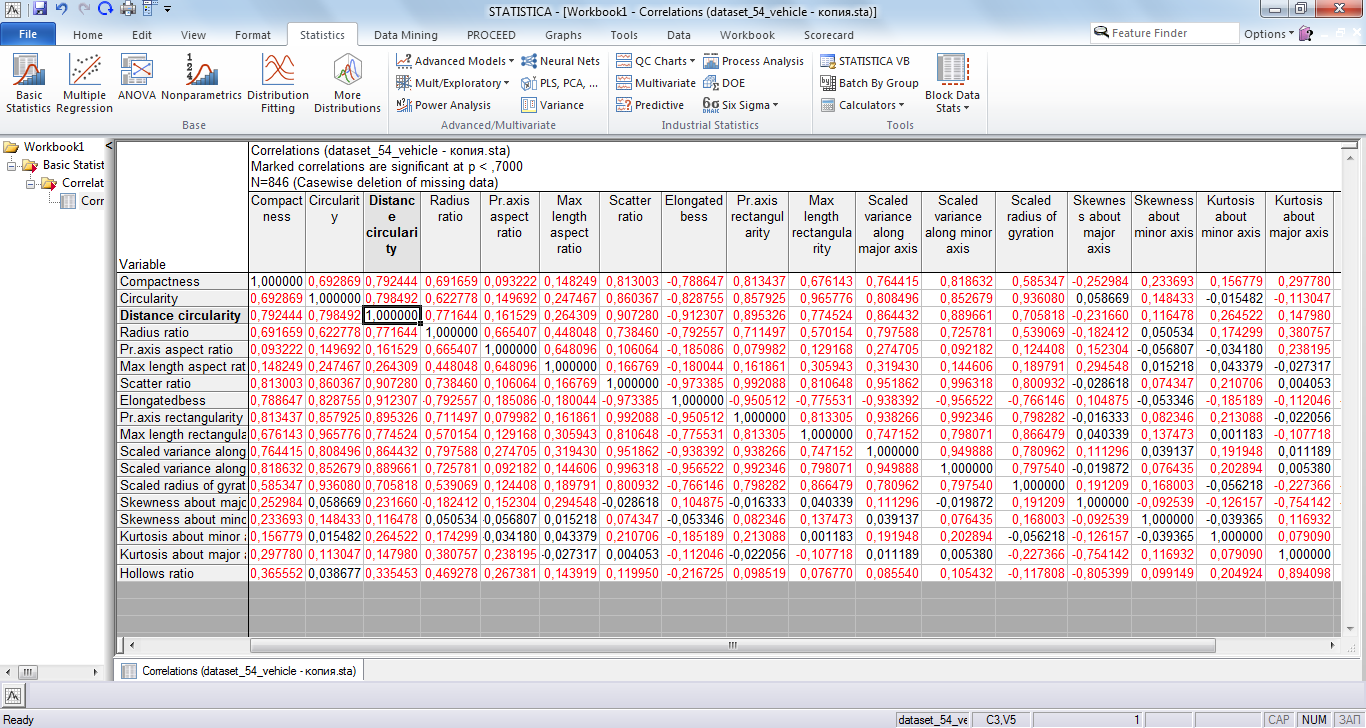
Рис 3. Корреляционная матрица
В результате проведения факторного анализа было выделено 4 фактора, факторные нагрузки для которых представлены на рисунке 4. Интерпретация выделенных факторов оказалась довольна затруднительна. Попытки использовать выделенные факторы в решении задачи классификации не привели к хорошему результату, об этом будет указано ниже при анализе результатов решения задачи классификации в STATISTICA.
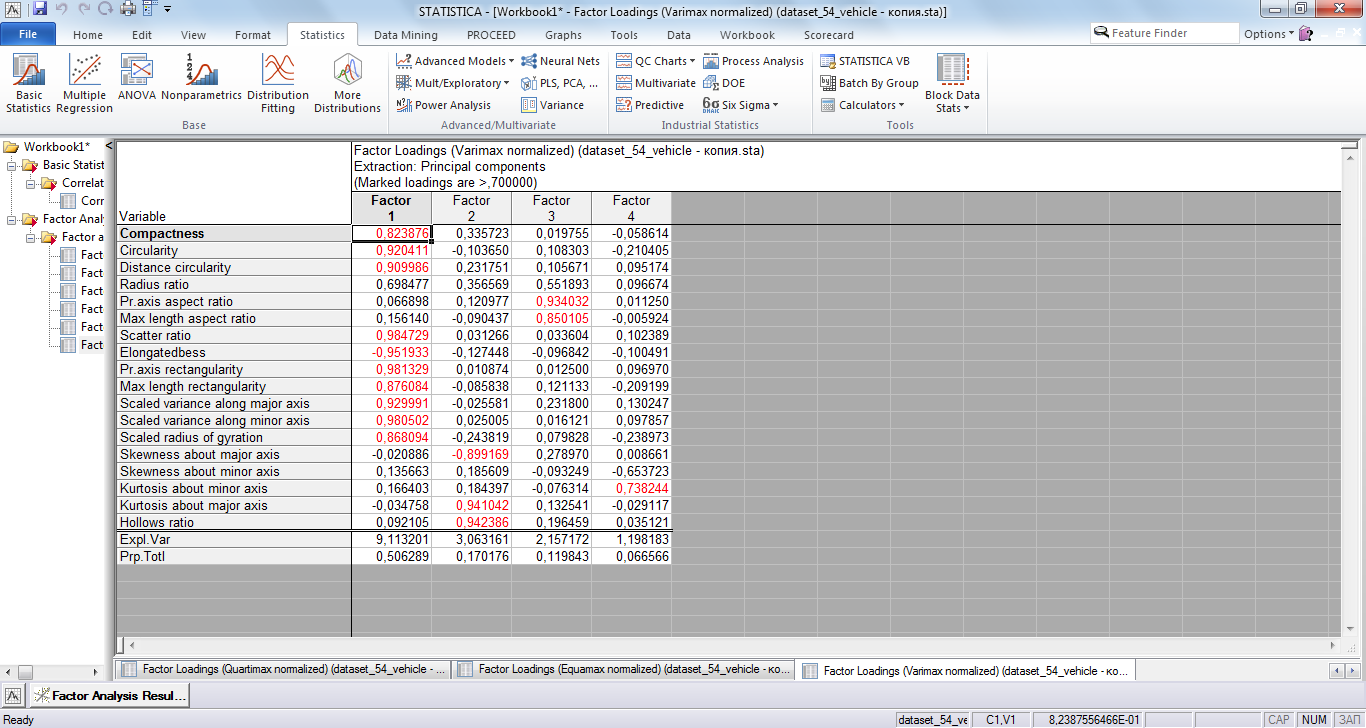
Рис 4. Факторные нагрузки
2 Описание метода
Задача классификации заключается в отнесении наблюдения с некоторым набором атрибутов к одному из нескольких заранее определённых классов. Классы определяются по множеству наблюдений, принадлежность к классам, для которых задана.
Нейронная сеть – набор взаимосвязанных элементов, так называемых нейронов. Каждый нейрон обладает входными синапсами и выходом – аксоном. Значения на синапсах умножаются на соответствующий весовой коэффициент и складываются, полученная сумма трансформируется специальной активационной функцией, которая обычно осуществляет отображения из интервала (-∞,+∞) в ограниченный интервал, обычно [0,1] или [-1,1]. Нейронная сеть позволяет осуществлять аппроксимацию различных многомерных функций. В задаче классификации в качестве выхода может служить как один нейрон с дифференциацией по значения, так и множество нейронов, значение на которых определяет степень принадлежности к классу, хотя возможны и другие варианты. По структуре нейронные сети делятся на сети различных типов, в данной работе используется тип многослойного перцептрона. Применение нейронных сетей для классификации происходит следующим образом. В начале сеть обучается на некоем известном множестве входов и выходов. Обучение заключается в настройке весов таким образом, чтобы уменьшить ошибку на обучающем множестве. После обучения, на вход сети подаётся наблюдение для классификации, по выходному значению определяется класс, к которому принадлежит наблюдений.
3 Решение задачи в STATISTICA
Используем автоматизированные нейронные сети для решения поставленной задачи классификации в пакете STATISTICA. Выходной является переменная “Класс”, все остальные переменные используются как входные.
Рис 5. Выбор переменных для анализа
Настроим разделение данных на 3 части случайным образом для обучения, тестирования и валидации полученных нейронных сетей. Соотношения размеров разделений представлены на рисунке 6.
Рис 6. Разделение данных
Укажем тип исследуемых сетей: MLP – многослойный перцептрон, количество нейронов в скрытых уровнях (от 5 до 17), количество проверяемых и отбираемых сетей (20 и 5), тип функций ошибок, используемых для обучения (сумма квадратов и перекрёстная энтропия).
Рис 7. Настройка параметров сети
Зададим типы активационных функций для скрытых слоёв нейронов и выходного слоя отдельно.
Рис 8. Выбор активационных функций
Запустим процесс обучения и выборки нейронных сетей. Две наилучшие сети представлены на рисунке 9.
![]()
Рис 9. Отобранные сети
Наилучший результат при валидации и тестировании получен нейросетью MLP 18-11-4. Наилучший результат при обучении получен нейросетью MLP 18-9-4. Обе сети используют гиперболический тангенс в качестве активационной функции для нейронов в скрытых слоях, различие заключается в количестве нейронов в скрытых слоях, алгоритме обучения, функции ошибки и функции активации нейронов выходного слоя.
Анализ чувствительности изображён на рисунке 10. По нему видно, что выбранные сети довольно сильно отличаются, во второй сети более равномерное распределение чувствительности, в то время как в первой наибольшее значение превосходит наименьшее где-то в 18 раз.
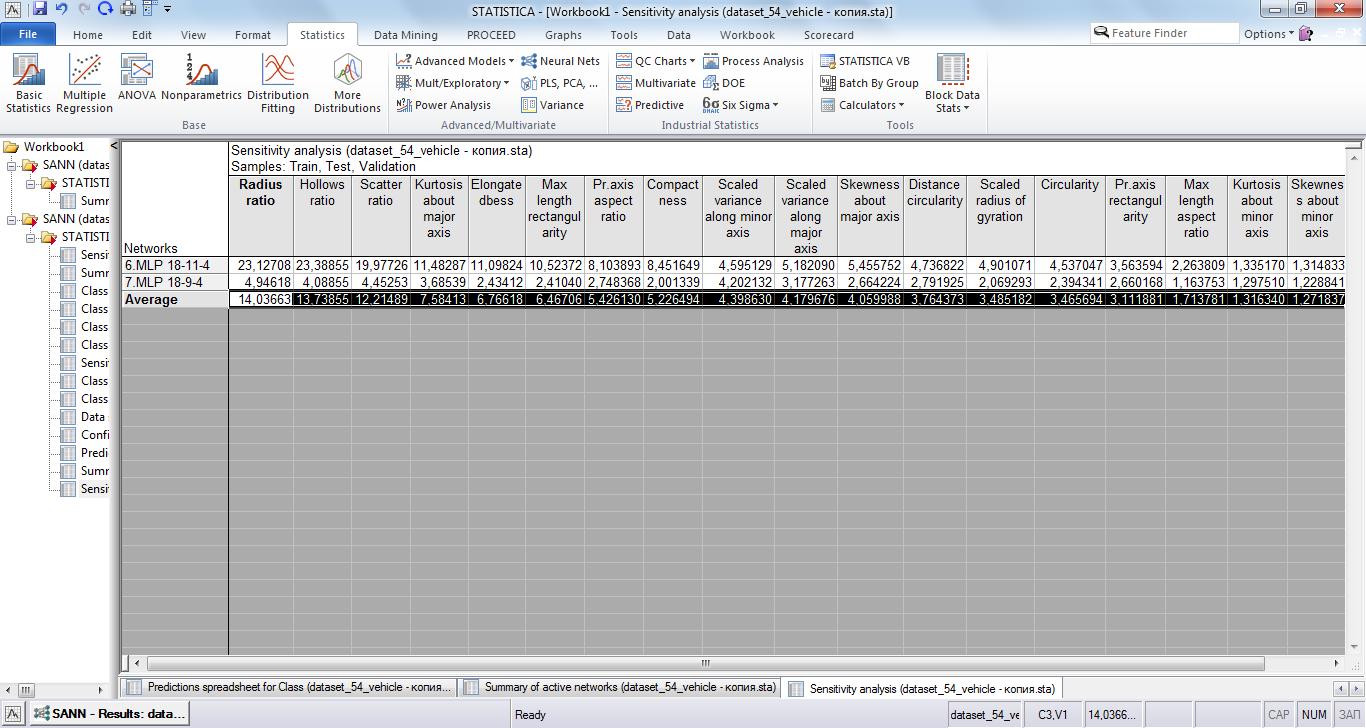
Рис 10. Анализ чувствительности
На рисунке 11 изображены результаты классификации в сумме по обучению, тестированию и валидации. Видно, что наибольшее количество некорректно определённых классов относится к классам “opel” и “saab”. При этом обе сети имеют примерно одинаковые показатели, несмотря на ранее рассмотренное различие в чувствительности к разным атрибутам.
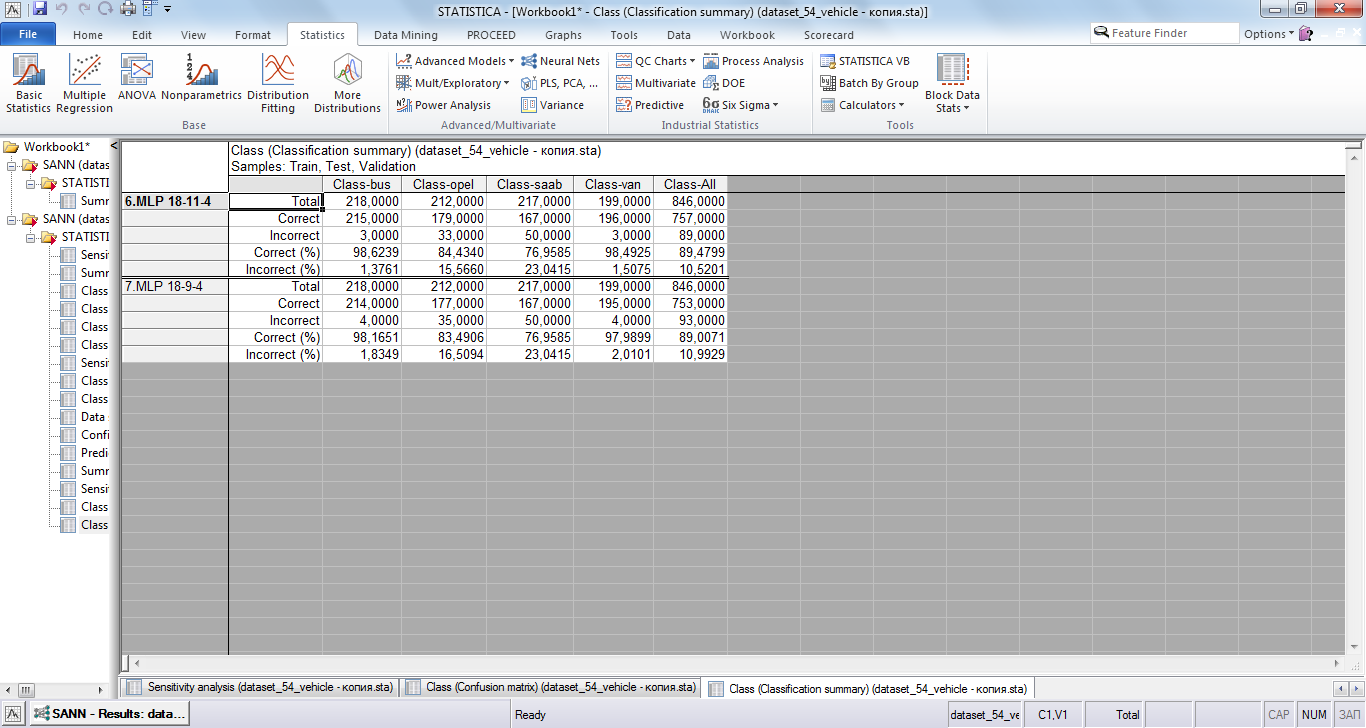
Рис 11. Сводка классификации
При попытке заменить атрибуты соответствующими им факторами точность классификации полученных нейронных сетей была довольно низкой, порядка 50%. При использовании лишь фактора с наибольшей объясняемой им дисперсий (то есть первого) вместо части атрибутов исходного массива данных наилучшими результатами были сети, показанные на рисунке 12.
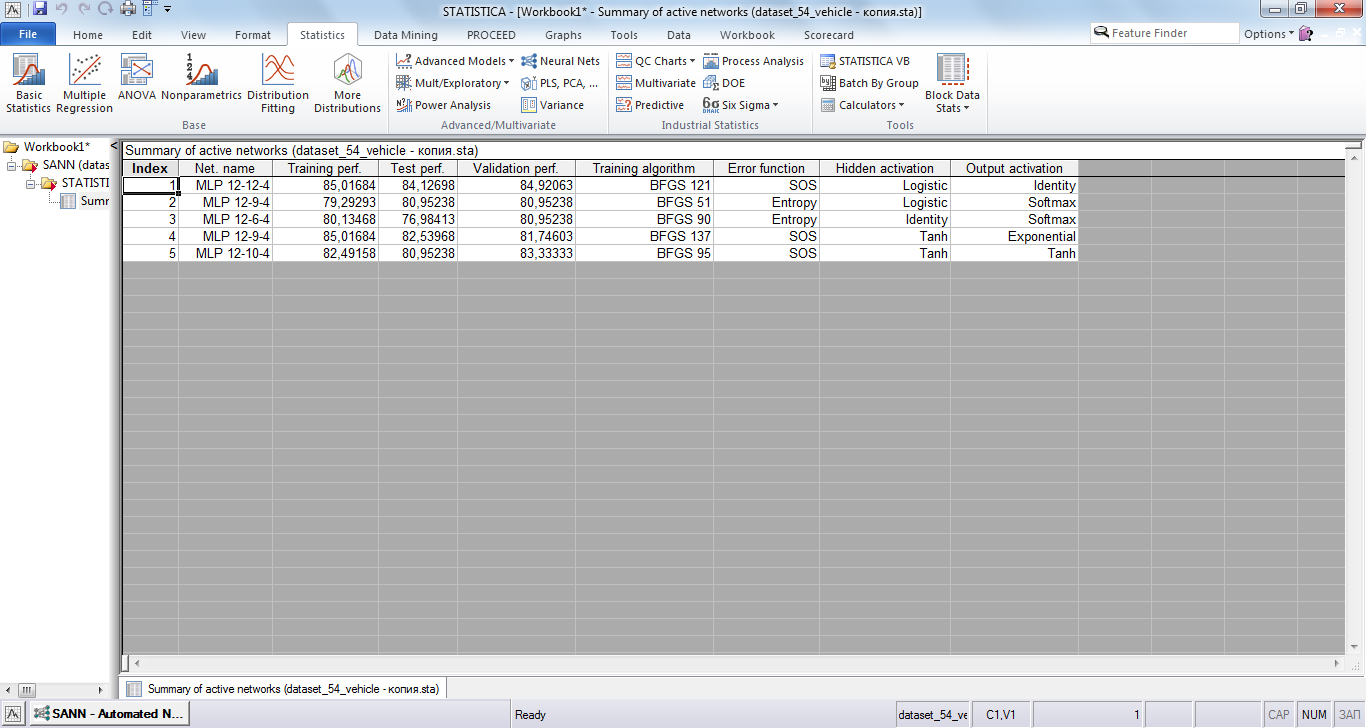
Рис 12. Наилучшие сети при попытке снижения размерности задачи
4 Решение задачи классификации в Deductor
Произведём обучение нейросети в программе Deductor. Так же, как и в случае использования пакета STATISTICA выберем переменную Class в качестве выходной, все остальные переменные будут использоваться в качестве входных (Рисунок 11). По умолчанию в Deductor для выходной переменной класса определяется по битам значения на выходе нейросети.
Рис 13. Выбор переменных
Разобьём исходный массив в соотношении 90 к 10 на обучающее и тестовое множества.
Рис 14. Разделение на обучающее и тестовое множества
Используем следующие настройки сети: кол-во слоёв 1, кол-во нейронов в слоях 18 – 8 – 2, функция активации – сигмоида с крутизной 1.5. В качестве алгоритма обучения используется алгоритм обратного распространения ошибки. Указанные параметры представлены на рисунках 15, 16 и 17.
Рис 15. Настройка структуры нейросети
Рис. 16. Выбор алгоритма обучения нейросети
Запустим обучение сети при заданных параметрах. Результаты показаны на рисунке 17.
Рис. 17. Результаты обучения сети
Как видно из рисунка, процент распознанных наблюдений довольно мал, а именно равен 69 процентам. Такие результаты не являются удовлетворительными, поэтому повторим процесс с другими параметрами.
Прежде всего поменяем нормализатор классовой переменной с битовой маски на уникальные значения (рисунок 18).
Рис. 18. Изменение нормализатора выходной переменной
Уменьшим крутизну сигмоиды до значения 1, количество нейронов в скрытом слое – 6. Также можно заметить, что Deductor автоматически уменьшил количество выходных нейронов до 1 (Рисунок 19).
Рис. 19 Настройка структуры нейронной сети
Проведём обучение нейронной сети с новыми параметрами.
Рис. 20 Результаты обучения
Как видно из рисунка 20, на этот раз результаты проверки обученной нейросети гораздо лучше – 92% распознано на тестовом множестве и 95% распознано на обучающем множество. На рисунке 21 представлена таблица сопряжённости, из неё видно, что наибольшее количество ошибок при классификации происходит у наблюдений, относящихся к классам “saab” и “opel”, причём нейросеть в основном путает их между собой, но в целом нейросеть работает довольно хорошо.
Обученная нейросеть некорректно классифицировала 93 наблюдения из 846, что примерно совпадает со значениями, полученными для лучших нейросетей в STATISTICA, то есть нейросети работают примерно на одном уровне, хотя данная нейросеть имеет более простую структуру.
Рис. 21 Таблица сопряжённости
Рис. 22 Статистика переменных
На рисунке 22 представлена статистика фактических и классифицированных значений класса для наблюдений, как можно увидеть, характеристики данных переменных довольно близки.
Теперь попробуем улучшить результаты изменив алгоритм обучения на алгоритм упругого распространения(Рисунок 23). Укажем в качестве функции активации гиперболический тангенс с крутизной 1. Количество скрытых нейронов – 5.
Рис. 23 Выбор алгоритма обучения сети
Результаты показаны на рисунках 24 и 25. Проценты распознанных наблюдений на обучающем и тестовом множествах вполне удовлетворительны: 92 и 86. Полученная нейросеть тоже имеет трудности при классификации классов “opel” и “saab”, возможно увеличений количества нейронов в скрытых слоях поможет уменьшить процент ошибок распознавания на этих классах. В целом количество некорректно распознанных классов больше чем в предыдущих вариантах.
Рис 24. Результаты обучения сети
Рис. 25 Таблица сопряжённости
Попробуем увеличить количество нейронов в скрытых слоях и число самих скрытых слоёв. Указанные параметры изображены на рисунке 26.
Рис. 26 Настройка структуры нейронной сети
Результаты представлены на рисунках 27 и 28. Данная нейросеть также имеет проблемы с распознаванием классов “opel” и “saab”, однако по сравнению с предыдущей сетью, данная сеть имеет меньшее количество некорректно распознанных моделей – 93, точно такое же число, что и в самой с 6 нейронами в скрытом слое и алгоритмом обратного распространения ошибки. На рисунке 29 изображена структура текущей сети, на ней можно увидеть синапсы нейронов сети, синапсы окрашены в цвет, показывающий значение веса.
Рис. 27 Результаты обучения сети
Рис. 28 Таблица сопряженности
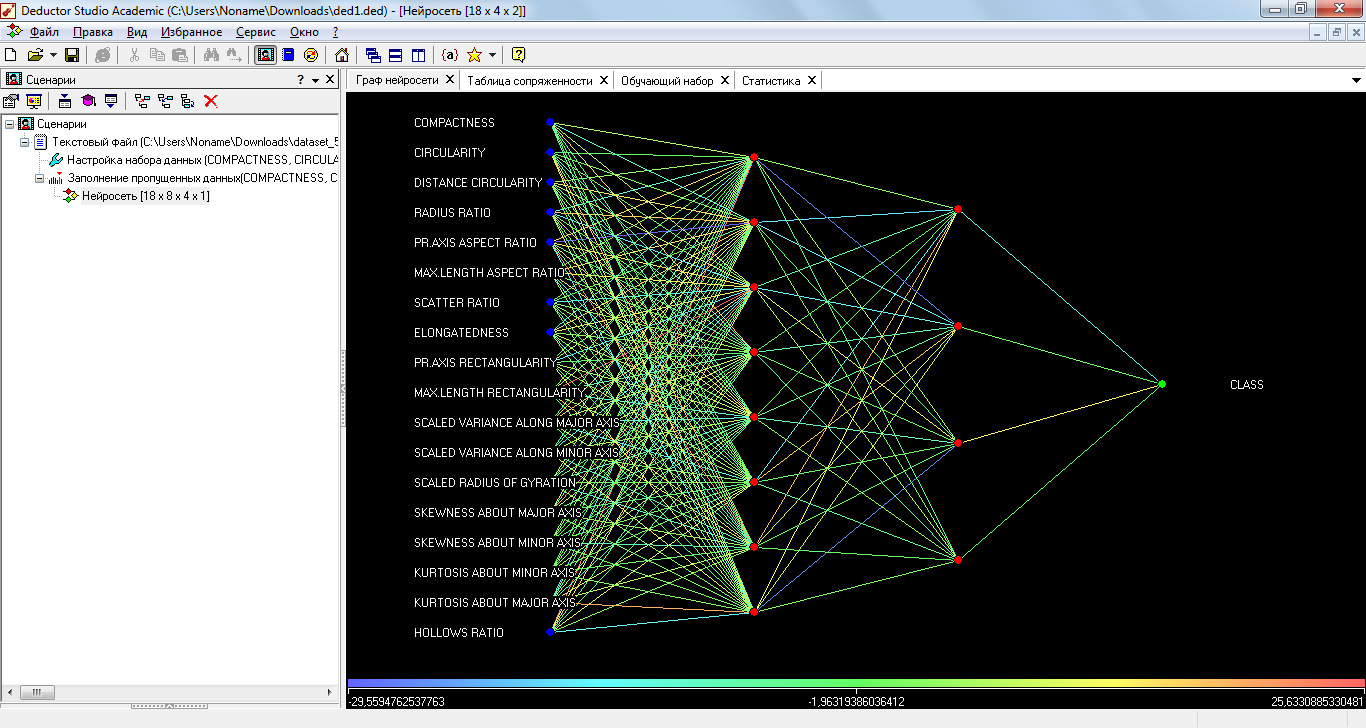
Рис. 29 Граф нейросети
5 Описание результатов
STATISTICA позволяет проводить автоматическое пакетное обучение нейросетей, что позволяет уменьшить время при классификации, также в ней имеются возможности для более тонкой настройки обучаемой нейросети, однако они не были рассмотрены в данной работе. Deductor имеет несколько настроек, не представленных в STATISTICA, однако работа в нём требует больших временных затрат. При решении конкретной поставленной задачи Deductor позволил получить нейросеть, показывающую результат, сравнимый с результатом, полученным в Statistica.
Вывод
В рамках данной работы было организовано решение задачи классификации моделей машин на основе параметров силуэтов в двух программных средах: STATISTICA и Deductor. С помощью обеих программных сред были получены нейросети, обеспечивающие хороший процент распознавания и работающие примерно на одном уровне. STATISTICA обладает более широким функционалом по сравнению с Deductor, хотя в данной задаче не удалось обнаружить большой разницы в полученных результатах.