ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 48
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
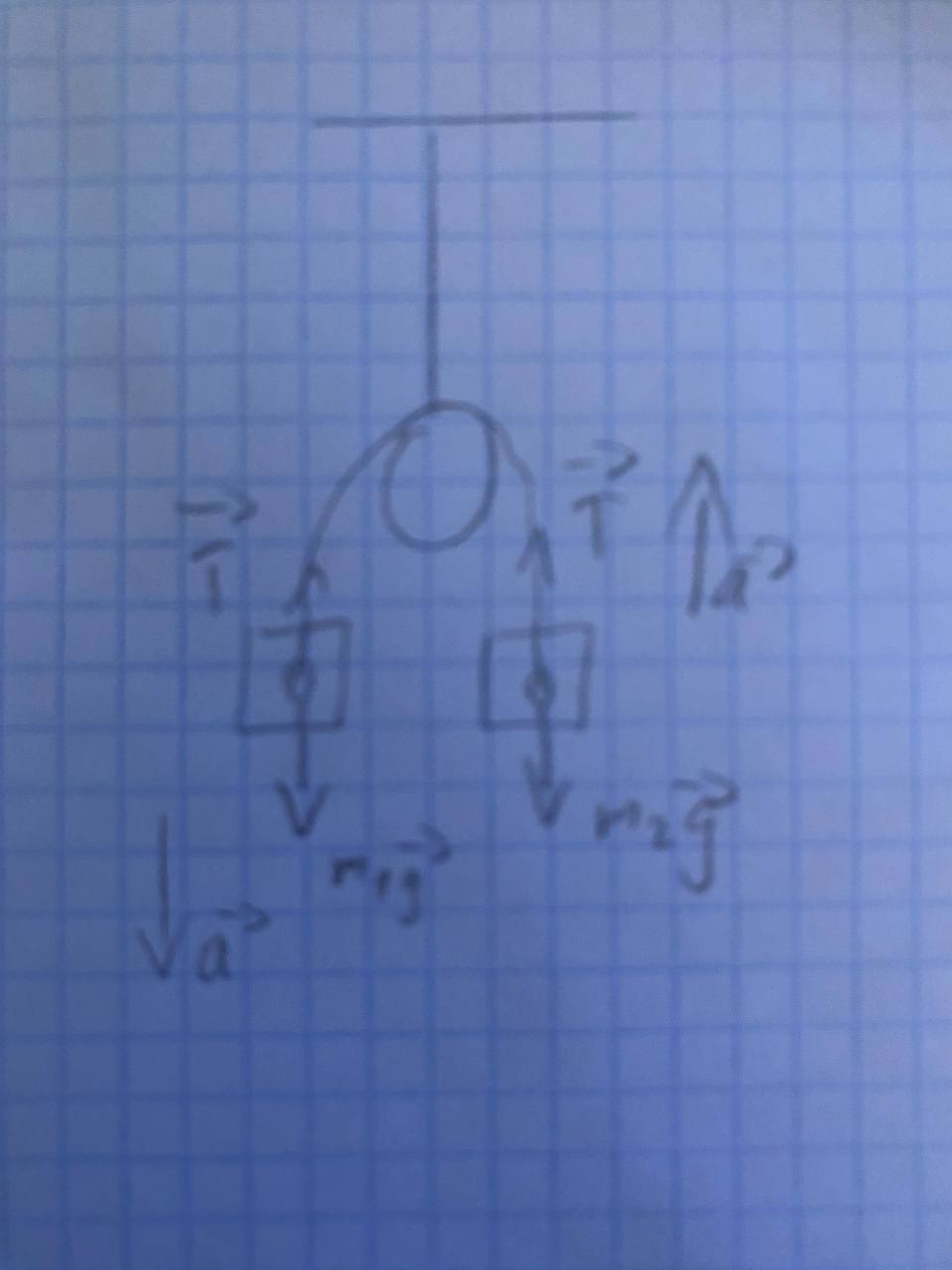
101* Два одинаковых груза массами m1= m2 = 0,5 кг связаны нитью, перекинутой через блок, укрепленный на конце стола (рис.1). Радиус блока R=0,2 м, масса блока m=1кг. Найти угловое ускорение блока, если коэффициент трения груза m2 о стол µ=0,2. Блок считать сплошным диском
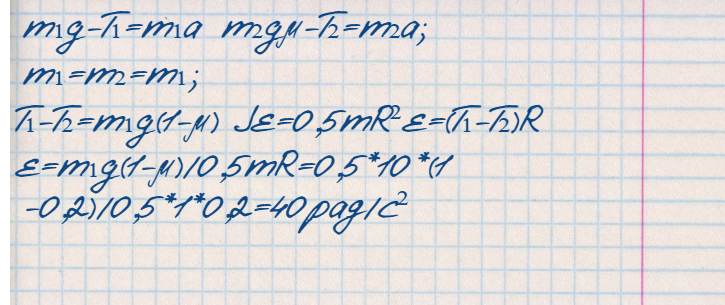
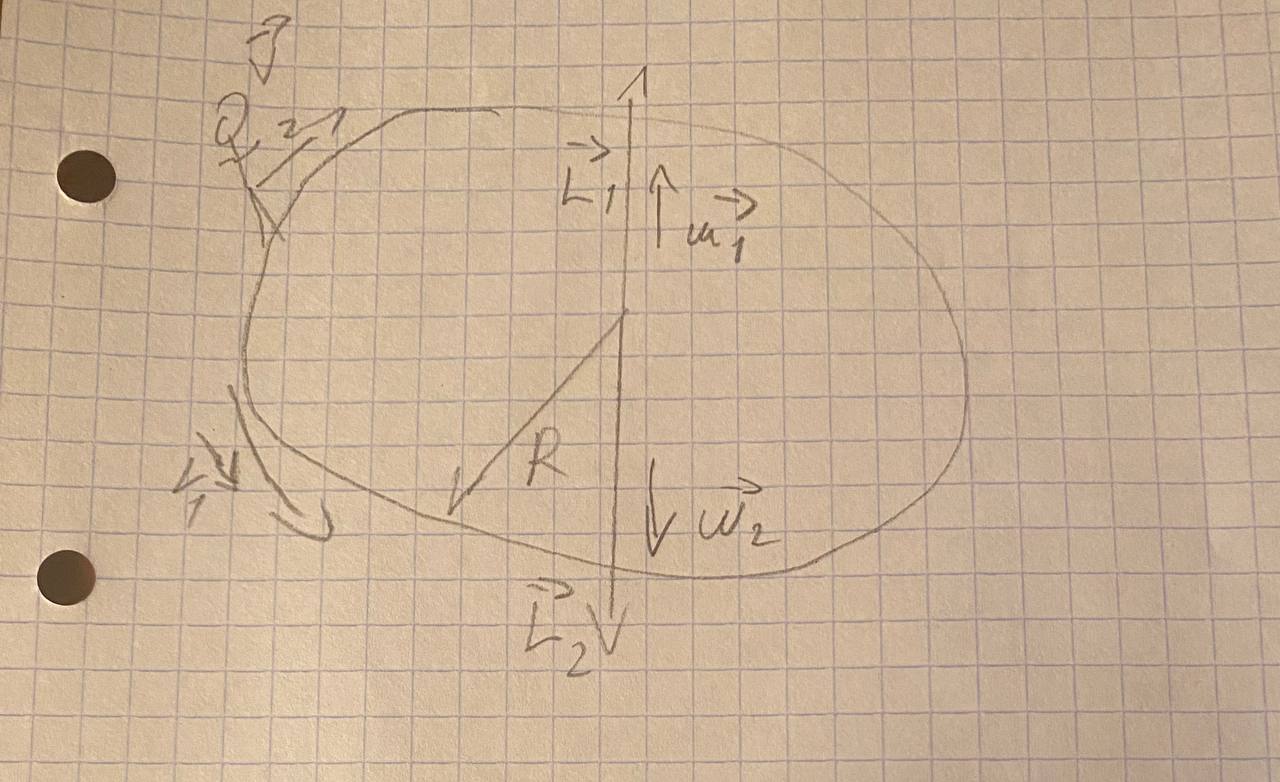
111* Платформа в виде горизонтально расположенного диска может вращаться вокруг вертикальной оси, проходящей через центр платформы. На платформе находится человек, которого в условии задачи можно рассматривать как материальную точку. Расходом энергии на преодоление сил трения пренебречь. Человек массой 60 кг стоит на краю платформы массой 120 кг, делающей 3,0 об/мин. Сколько оборотов в минуту будет делать платформа, если человек перейдет на середину между краем и центром платформы?

121* Два одинаковых заряженных шарика подвешены в одной точке на нитях одинаковой длины. При этом нити разошлись на угол α. Шарики погружаются в масло плотностью ρ=8.102 кг/м8. Какова диэлектрическая проницаемость ε масла, если угол расхождения нитей при погружении шариков в масло остается неизменным? Плотность материалов шариков ρ=1,6.103 кг/м3.
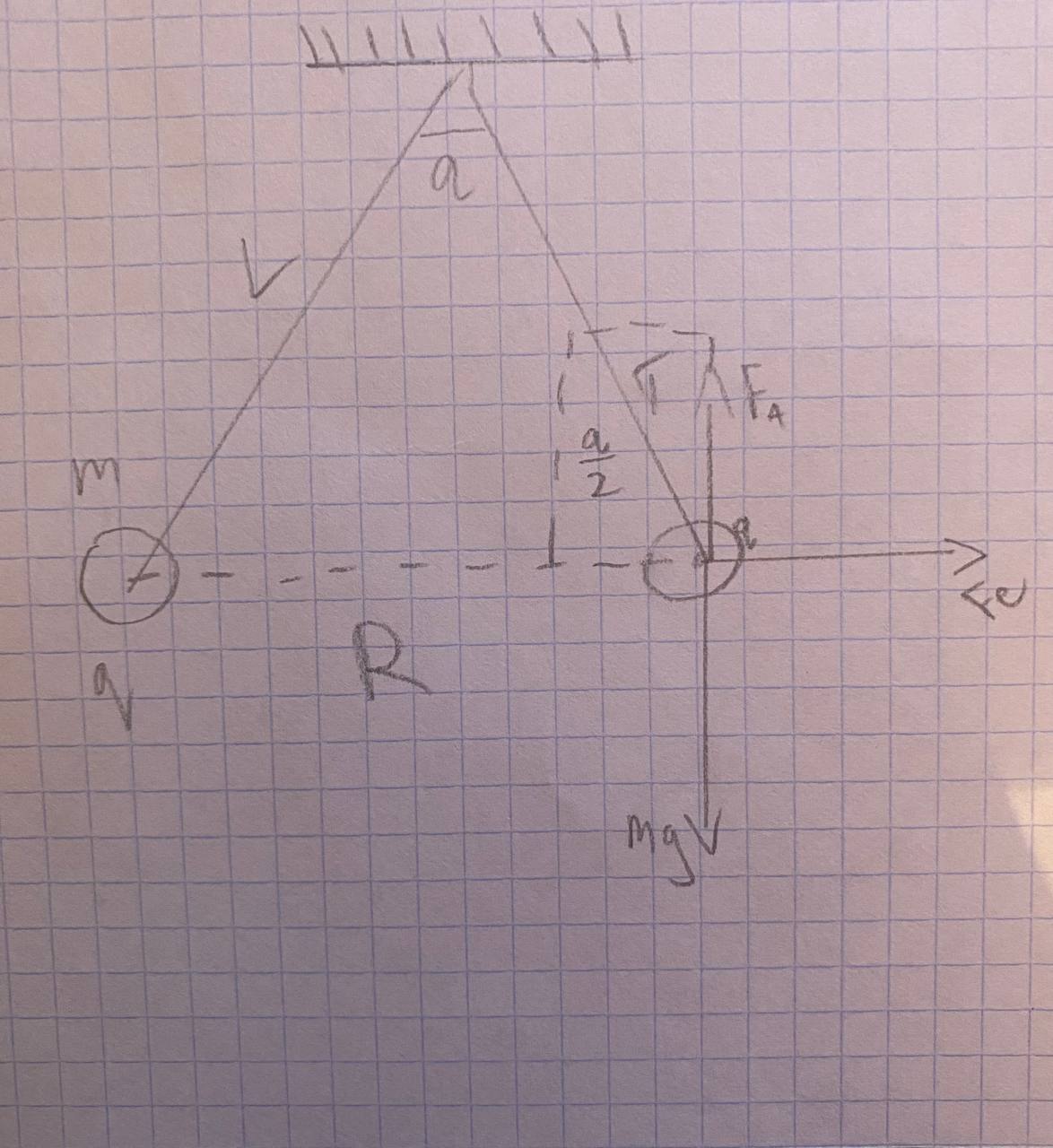
F⃗ +F⃗ A+T⃗ +mg⃗ =0F→+F→A+T→+mg→=0
1/4πϵ0*Q1Q/2r^2=x1
Fк=x/ϵ
1)вариант:
FA1=0; ϵ=1; FA1=0;ϵ=1
x:−Fк1+T1sinα2=0
x:−Fк1+T1sinα/2=0
y:T1cosα/2−mg=0
{T1=mg/cos(α/2)
{−Fк1+mgtgα/2=0
tgα/2 = Fк1/mg = x/mg ϵ=
2) вариант:
x:−Fк2+T2sinα2=0x
y:FA2+T2cosα2−mg=0
{T2=Fк2/sin(α/2)
{FA2+Fк2tgα2−mg=0 (4)
m=ρV (5)
FA2=ρ0gV (6)
Подставим (2),(3),(5) и (6) в (4):
ρ0gV+xϵρVgx−ρVg=0
ρ0+ρ/ϵ−ρ=0
ρ=ϵ(ρ−ρ0)
ϵ=ρ/ρ−ρ0
ϵ=1,6⋅10^3/1,6⋅10^3−8⋅10^2=2
131* Между двумя бесконечно длинными, коаксиальными и разноименно заряженными цилиндрическими поверхностями малых радиусов R1 = 4 см и R2 = 10 см находится слой диэлектрика ( ε = 3), прилегающего к цилиндрической поверхности большего радиуса R2 . Меньший радиус диэлектрического слоя R0 = 7 см. Линейная плотность заряда поверхности радиусом R1 составляет -3 нКл/м, а внешней поверхности радиусом R2 - + 3 нКл/м. Построить графики функций f1(r) и f2(r) для случаев:
I) r
Вычислить разность потенциалов ∆φ между точками r1=4 см и r2= 9 см.
1) Внутри обоих цилиндров (r < R1) результирующая напряженность поля
Е = 0;
электрическое смещение
D = εε0Е = 0.
2) Между цилиндрами результирующая напряженность поля:
в области без диэлектрика (R1 ≤ r ≤ R0)
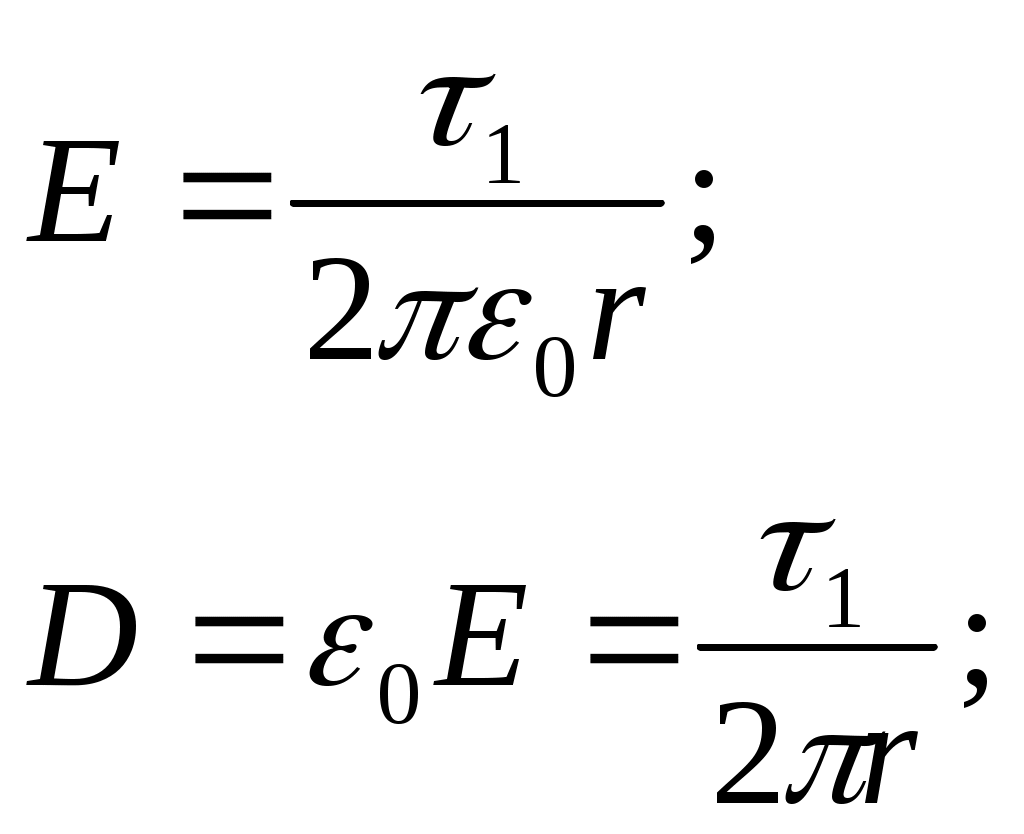
в области с диэлектриком (R0 < r ≤ R2)
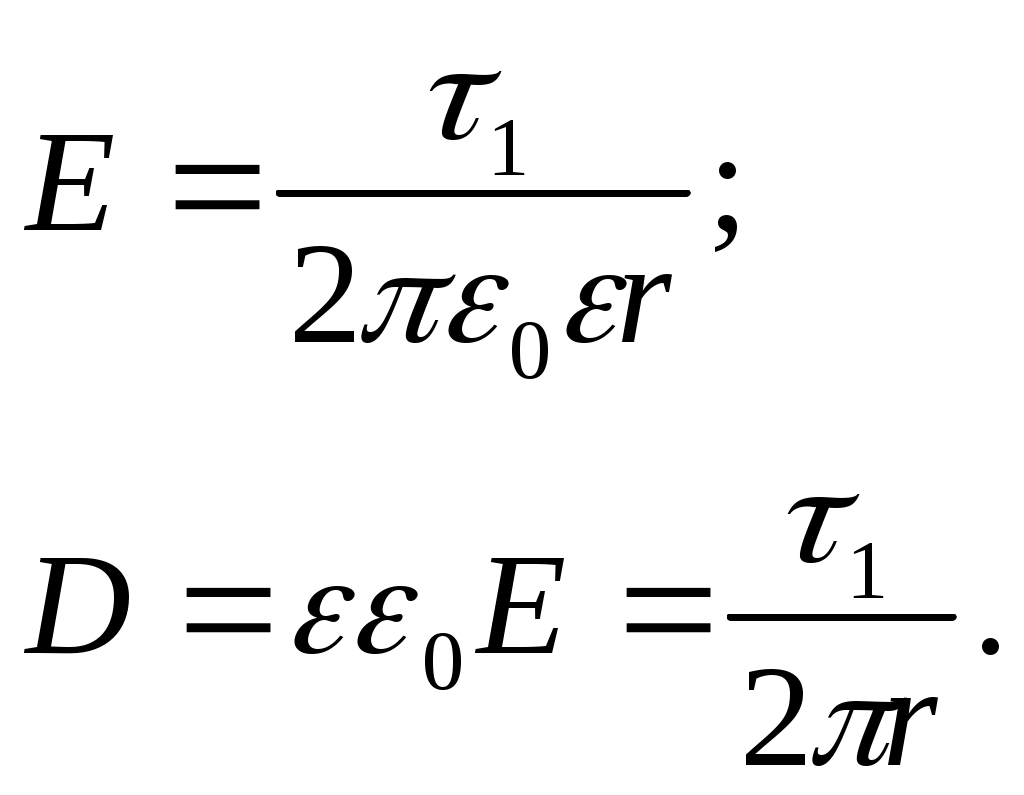
3) Вне цилиндров (r > R2)
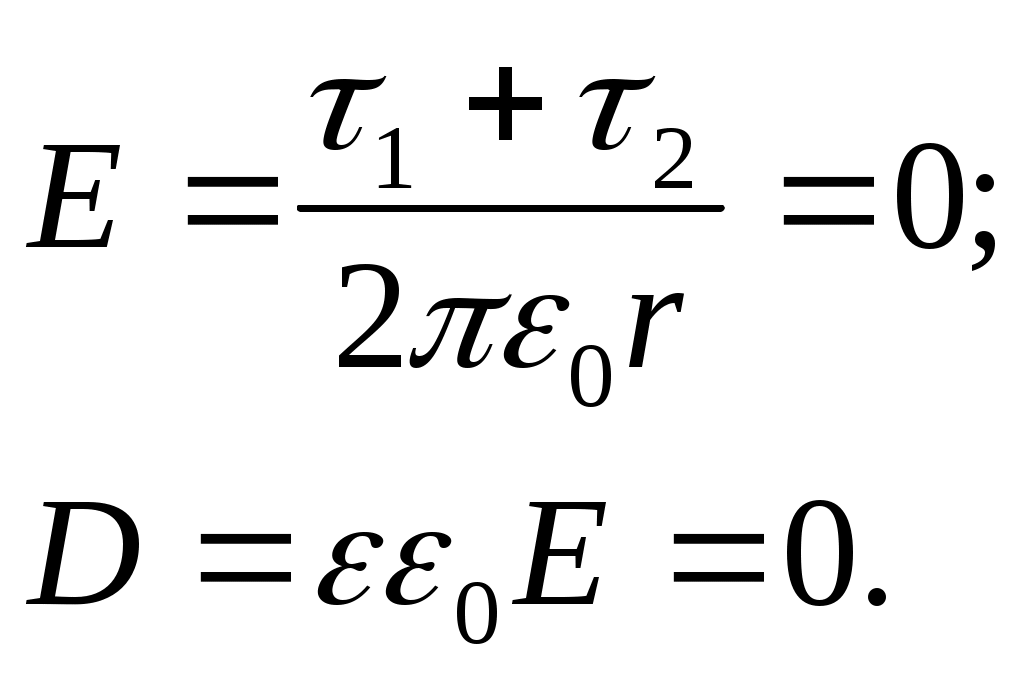
Для построения графиков E(r) и D(r) вычислим значения E и D в характерных точках (r = 7–0 см — это значение r чуть меньшее, чем r = 7 см):
| r, см | 0 | 4–0 | 4+0 | 7–0 | 7+0 | 10–0 | 10+0 |
| E, В/м | 0 | 0 | –1350 | –771 | –257 | –180 | 0 |
| D, нКл/м2 | 0 | 0 | –12 | –6,8 | –6,8 | –4,8 | 0 |
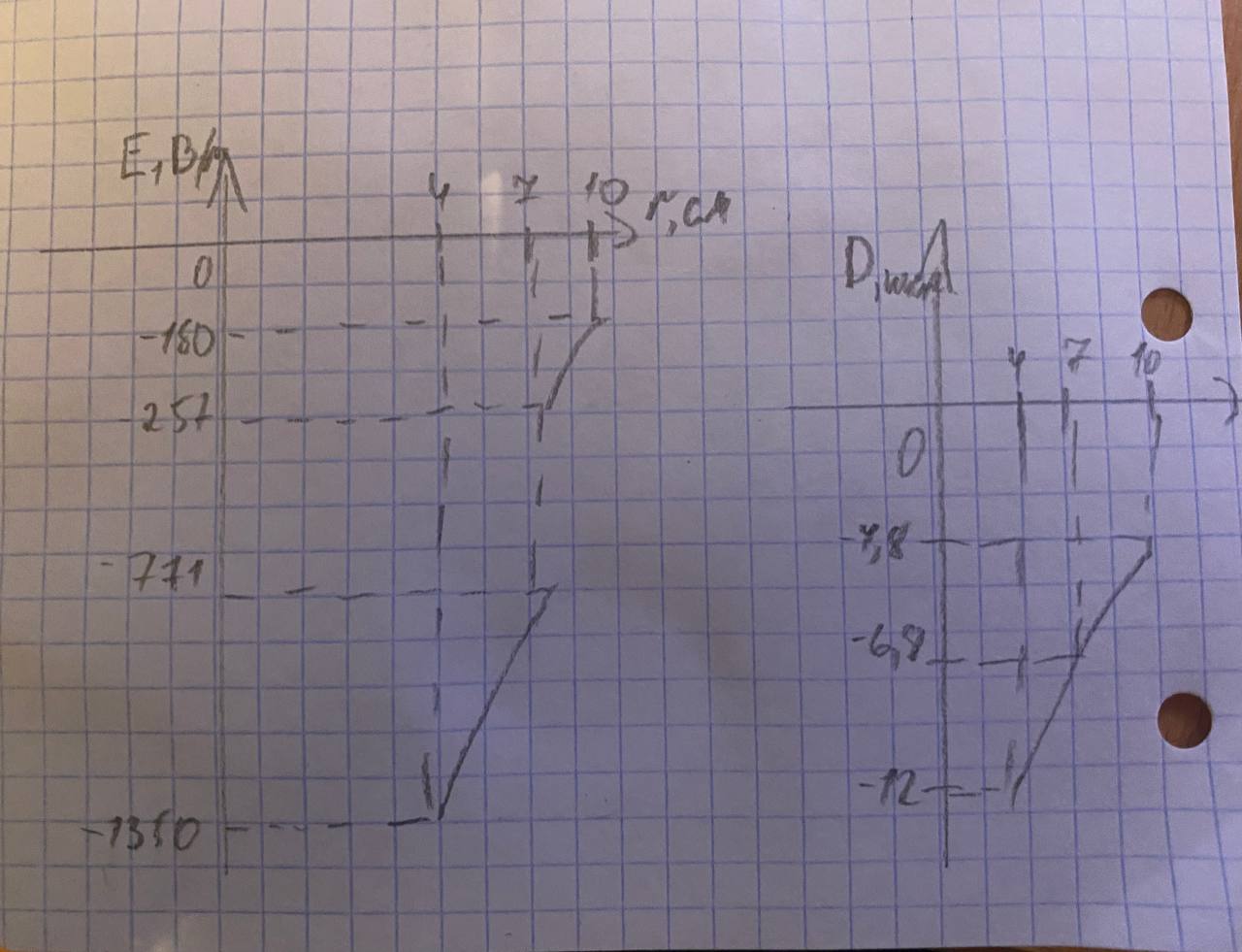
Найдем разность потенциалов между точками r1 = 4 см и r2 = 9 см по формуле
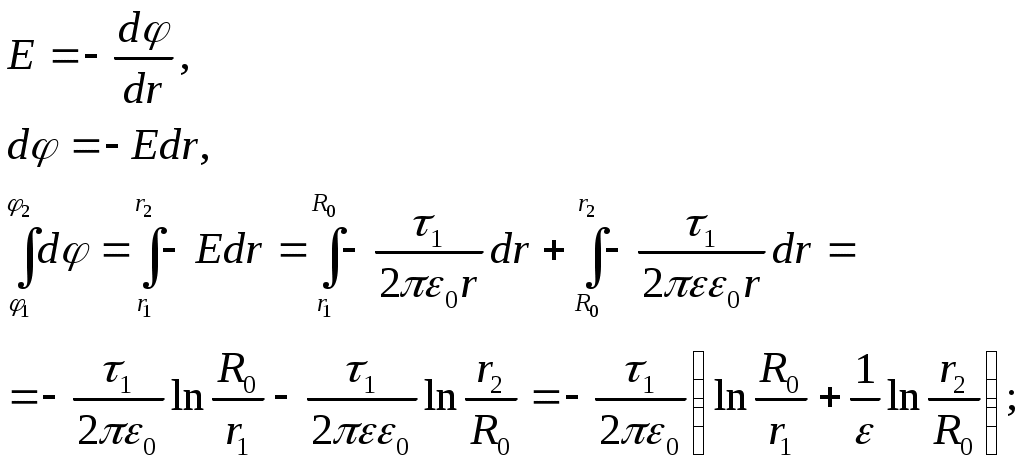
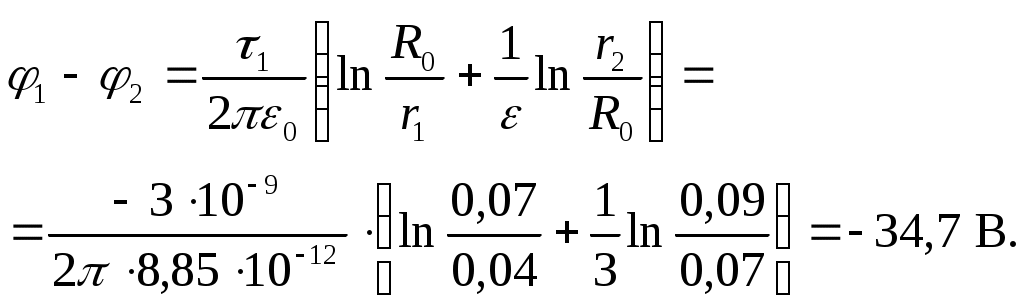
φ1–φ2 = –34,7 В.
141 Определить проводимость и удельную тепловую мощность тока в проводнике с концентрацией электронов n=8.1028 м-3 и средней дрейфовой скоростью u = 2,8.10-2 см/с, если разность потенциалов ∆φ двух точек однородного электрического поля в проводнике, отстоящих на l = 2.2 мм друг от друга, составила 1,4.10-4 В.
Напряженность электрического поля E = 1.4*10^-4 В / (0.0022 м) = 0.0(63) В/м
Заряд, протекающий через площадь S за время t, q = e*n*u*S*t
Плотность тока J = I/S = q/(t*S) = e*n*u = 1.6*10^-19 Кл * 8*10^28 м-3 * 2.8*10^-4 м/с = 3.584*10^4 А/м2
Проводимость σ = J/E = 3.584*10^4 / 0.0(63) = 5.632*10^5 1/(Ом*с)
Удельная тепловая мощность ω = jE2=3.584*10^4*(0.0(63))2 = 142( Дж*сек) /(см2)

151* Бесконечный прямолинейный провод на некотором участке образует петлю в виде равностороннего треугольника, вершина которого находится на самой прямой, а его основание длиной 10 см параллельно ей. Найти магнитную индукцию в центре петли, если по проводу протекает ток силой 30 А.
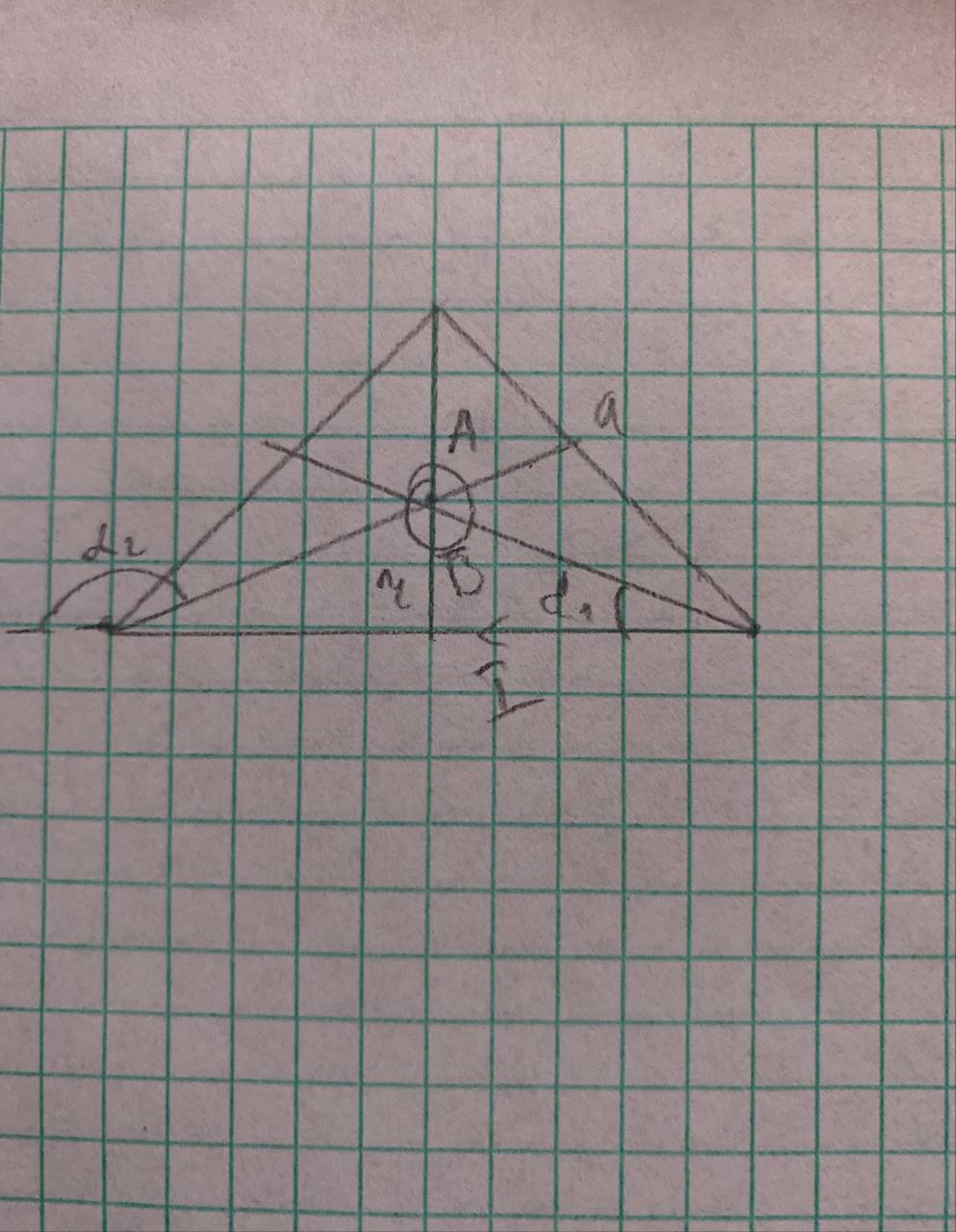
B0 = 3B = B1 + B2 + B3
B1 = (uu0/4 π) * (2I /atg10o) * (cos10o-cos170o)
B = (3*4 π *10-7*1/4 π )* (2 * 30/0,1 * 0,1763) * (0,984 + 0,984) = 0,000062 Тл = 0,62 мТл
