ПАРНАЯ РЕГРЕССИЯ1. В таблице приведены данные, опубликованные в марте 1984 года в журнале Wall Street и иллюстрирующие взаимосвязь между расходами на рекламу (в миллионах долларов) 21 фирмы за 1983 год и миллионами отзывов, оставляемых потребителями продукции этих фирм в среднем за неделю.

Компания	Отзывы, млн.	Расходы на рекламу (млн. дол.)
Miller Lite	32.1	50.1
Pepsi	99.6	74.1
Stroh’s	11.7	19.3
Fed’I Express	21.9	22.9
Burger King	60.8	82.4
Coca Cola	78.6	40.1
McDonald’s	92.4	185.9
MCI	50.7	26.9
Diet Cola	21.4	20.4
Ford	40.1	166.2
Levi’s	40.8	27.0
Bud Lite	10.4	45.6
ATT/ Bell	88.9	154.9
Calvin Klein	12.0	5.0
Wendy’s	29.2	49.7
Polaroid	38.0	26.9
Shasta	10.0	5.7
Meow Mix	12.3	7.6
Oscar Meyer	23.4	9.2
Crest	71.1	32.4
Kibbles ‘N Bits	4.4	6.1

---

1. 
   Постройте график, отложив на вертикальной оси «Отзывы» и «Расходы на рекламу» по горизонтали.
   

2. 
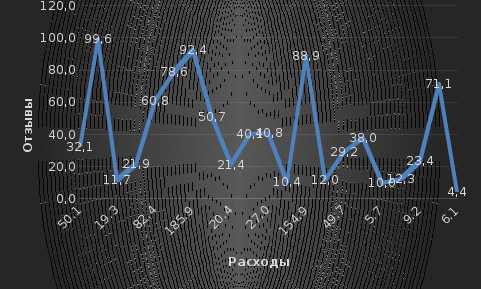
   Связь между признаками прямая, поскольку с увеличением расходов на рекламу увеличиваются отзывы потребителей.
   

с) Оправданы. Так как видна тенденция увеличения отзывов с увеличением расходов на рекламу.2. Исследуется зависимость объема продаж бензина от динамики потребительских цен. Были получены следующие данные по 9 регионам:

Квартал	1	2	3	4	5	6	7	8	9
Индекс потребительских цен (в %) Х	139	132	126	121	117	112	106	100	100
Средний за день объем продаж бензина в течение квартала (тыс. л.) Y	65	68	72	75	77	80	83	85	89

1. 
   Построить поле корреляции результативного и факторного признаков (график), сделать вывод о форме связи между ними.
   

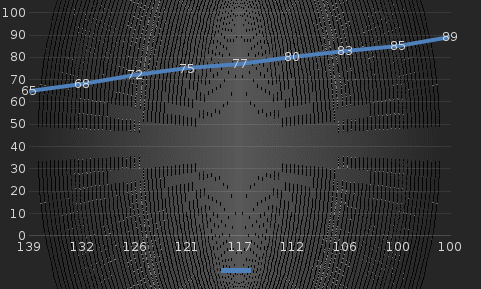
Вывод: Связь между объемом продаж бензина и потребительскими ценами обратная (С увеличением Х, уменьшается Y – из 2 в 4 четверть).

2. 
   Рассчитать линейный коэффициент корреляции; среднее квадратическое отклонение
   

x	y	x-xср	y-yср		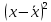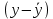2	xy	(x-xср)(y-yср)
139	65	22	-12,11	484	146,6521	9035	-266,42
132	68	15	-9,11	225	82,9921	8976	-136,65
126	72	9	-5,11	81	26,1121	9072	-45,99
121	75	4	-2,11	16	4,4521	9075	-8,44
117	77	0	-0,11	0	0,0121	9009	0
112	80	-5	2,88	25	8,2944	8960	-14,4
106	83	-11	5,89	121	34,6921	8798	-64,79
100	85	-17	7,89	289	62,2521	8500	-134,13
100	89	-17	11,89	289	141,3721	8900	-202,13
1053	694			1530	506,8312	80325	-872,95
117	77,11			170	56,31458	8925

---

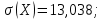
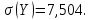
Var(x)= 170;Var(y) = 56,31458;Среднее квадратическое отклонение:r_xy=–872,95/ 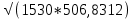= - 0,99131612 - коэффициент корреляции0,7< r_{xy <1}

3. 
   Вывод:
   

Коэффициент корреляции между количеством продаваемого товара и ценой за единицу обратный и имеет сильную степень связи (коэффициент корреляции близок к -1). Это означает, что с увеличением цены продажи количество продаваемого товара снижается, а при снижении цены количество продаваемого товара увеличивается. Также можно заметить, что наблюдения не равномерно распределены вдоль линии регрессии, что может указывать на наличие других факторов, влияющих на спрос на товар, помимо цены.

---

Смотрите также файлы

• Для железодефицитной анемии характерно a нормохромная анемия.docx

• Средства индивидуальной защиты органов дыхания.docx

• Химический состав в материала 40хнр.docx

• Методы культурологического исследования.docx

• По эскизу детали разработайте эскиз отливки с модельно литейными указаниями, приведите эскизы модели, стержневого ящика и собранной литейной формы в разрезе Опишите последовательность изготовления формы методом ручной формовки.doc