Федеральное агентство связи ОрденаТрудового Красного Знаменифедеральное бюджетное образовательное учреждение высшего образования«Московский Технический Университет Связи и Информатики»(МТУСИ)Кафедра ИнформатикиПредмет: Численные методыЛабораторная работа № 1Тема:

«Методы решения нелинейных уравнений»

Вариант 22Выполнил: Иван ИвановОбщее задание

1. 
   Выбрать индивидуальное задание из табл. 1-1:
   

• 
  нелинейное уравнение;
  
• 
  методы решения нелинейного уравнения для выполнения 3-х итераций;
  

1. 
   Отделить корни заданного уравнения графическим и аналитическим методом с использованием средств пакета Mathcad.
   

1. 
   Для каждого из заданных методов провести исследование функции нелинейного уравнения:
   

• 
  проверить выполнение условий сходимости вычислительного процесса, в случае расходящегося процесса – сделать необходимые преобразования для обеспечения сходимости;
  
• 
  выбрать начальное приближение к корню;
  
• 
  сформулировать условие окончания этапа уточнения корня.
  

1. 
   С использованием итерационной формуле 1-го заданного методу провести расчет трех итераций с использованием средств мат. пакета. Результаты расчета свести в табл. 1-2.
   

1. 
   Оценить погрешность результата после 3-х итераций.
   

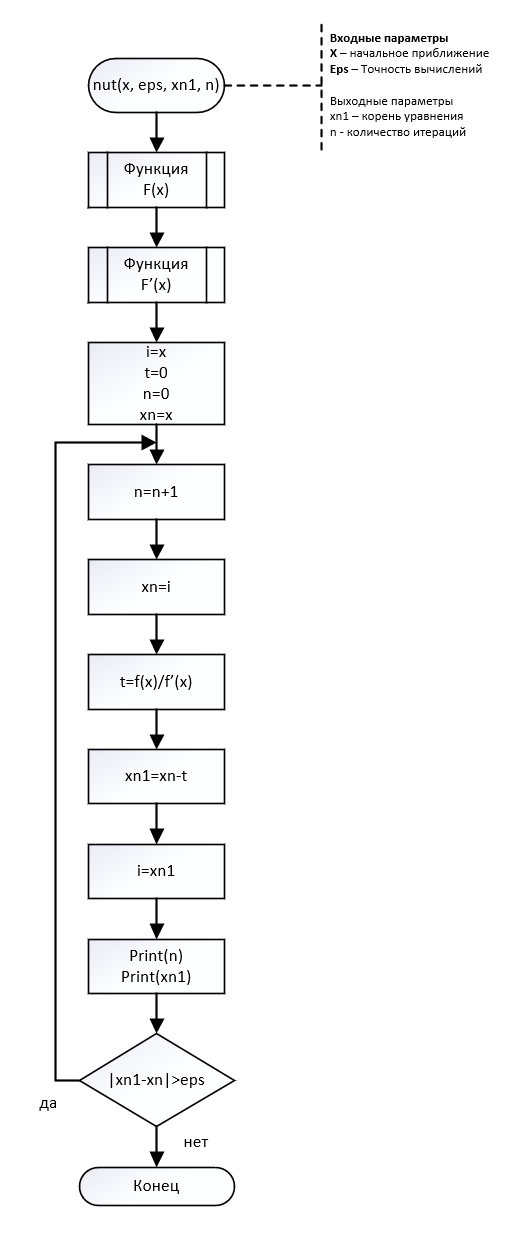
Для 2-го заданного метода выполнить решение уравнения с точностью 10^-4, создав программу, реализующую заданный метод. Произвести расчет, а результаты решений свести в табл. 1-2.Индивидуальное заданиепервый заданный метод — метод Ньютонавторой заданный метод – метод итерацииПервый этап - отделение корней

---

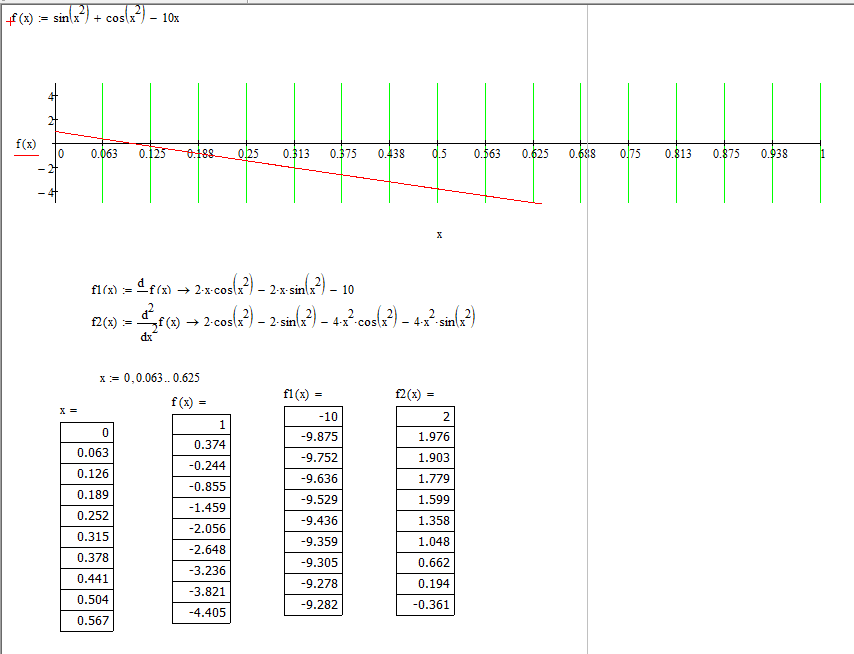
Из построенного графика функции видно, что на отрезке (0;0.625) есть один корень.Второй этап – ручной расчетВоспользуемся методом Ньютона.

k	Xk	f(xk)
0	0	1
1	0.1	9.95*10-3
2	0.10101508097	9.99*10-7
3	0.10101518291	9.992*10-15

Третий этап – расчет с использованием программыВоспользуемся методом простых итерацийКод программы:import mathx = float(input('Введите начальное приближение: '))eps = float(input('Введите необходимое значение точности: '))def f(x): #заданная функцияreturn 4*(x*x+1)*math.log(x, math.e)-1def f1(x): #функция первой производнойreturn 8*x*math.log(x, math.e)+4*x+4/xi = xt = 0n = 0xn = xxn1 = 0while abs(xn1-xn) > eps:n += 1xn = it = f(xn)/f1(xn)xn1 = xn - ti = xn1print("│ кол-воитераций: " + str(n) + " │ значениекорня: " + str(xn1))breakРезультат работы программы:Введите начальное приближение: 1Введите необходимое значение точности: 0.0001│ кол-во итераций: 1 │ значение корня: 1.125│ кол-во итераций: 2 │ значение корня: 1.1176051231553725│ кол-во итераций: 3 │ значение корня: 1.1175756445147635Вычисленное значение корня на калькуляторе: x = 1.11757564404935Вычисленное значение корня с помощью программы: X = 1.1175756445147635Всего за три итерации мы достигли точности аж до 9 знака после запятой.

---

Смотрите также файлы

• Инструкция по выполнению задание выполняется, опираясь на лекции по Разделу ii (темы 913), материалам основной и дополнительной литературы..docx

• Исследование биоритмов учащихся 89 классов моу сош 1 р п. Дергачи.docx

• Детство является уникальным периодом в жизни человека. Именно с детства формируется здоровье, происходит становление человека. Опыт детства во многом определяет взрослую жизнь человека.docx

• Уверенное владение навыками чтения и письма является одним из основных условий успешности детей в учении.doc

• Пояснительная записка по предмету История Казахстана.docx