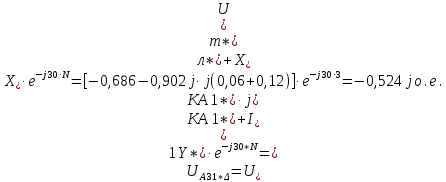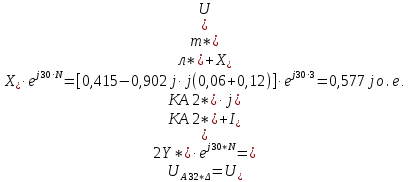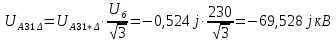Файл: Отчет по лабораторной работе 2 распределение симметричных составляющих напряжений при несимметричных коротких замыканиях.docx
Добавлен: 12.01.2024
Просмотров: 53
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Федеральное государственное автономное образовательное учреждение
высшего образования
«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

Инженерная школа энергетики
Отделение электроэнергетики и электротехники
Направление − 13.03.02 Электроэнергетика и электротехника
Отчет
по лабораторной работе №2
РАСПРЕДЕЛЕНИЕ СИММЕТРИЧНЫХ СОСТАВЛЯЮЩИХ НАПРЯЖЕНИЙ ПРИ
НЕСИММЕТРИЧНЫХ КОРОТКИХ ЗАМЫКАНИЯХ
Вариант №10
| Выполнил: | | Тюленев Данила Алексеевич |
| студент группы: 5А98 | (подпись, дата) | (Ф.И.О) |
| Проверил | | Вымпина Юлия Николаевна |
| преподаватель: | (подпись, дата) | (Ф.И.О) |
Томск 2023 г.
Цель работы:
Исследовать закономерности распределения симметричных составляющих остаточных напряжений в узлах схемы при несимметричных коротких замыканиях (КЗ).
Общие положения и расчетные выражения:
Несимметричные КЗ в электрических системах приводят к нарушению симметрии фазных и линейных величин токов и напряжений. Моделирование несимметричных режимов можно осуществить методом симметричных составляющих, используя системы прямой, обратной и нулевой последовательностей. Тогда интересуемые несимметричные величины фазных токов и напряжений будут представлены геометрической суммой соответственно токов и напряжений прямой, обратной и нулевой последовательностей. Согласно принципу независимости действия симметричных составляющих, каждая из трех последовательностей может рассматриваться автономно.
Для симметричных составляющих остаточных напряжений двух соседних узлов i и j, связанных между собой в схеме прямой последовательности через
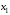 и в схеме обратной и нулевой последовательностей соответственно через
и в схеме обратной и нулевой последовательностей соответственно через 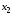 и
и 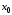 , справедливы уравнения Кирхгофа (в относительных единицах):
, справедливы уравнения Кирхгофа (в относительных единицах): 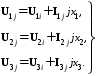
Положительное направление тока принято от узла j к узлу i.
Эти уравнения (1) и определяют характер распределения симметричных составляющих напряжений в схеме в зависимости от симметричных составляющих токов и соответствующих значений сопротивлений элементов для различных последовательностей токов.
Фазные значения напряжений определяются геометрической суммой ее симметричных составляющих:
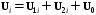 ,
, где i = А, В, С – индекс фазы.
Для перевода фазных величин напряжения (равно как и симметричных составляющих) из относительных единиц в именованные используют коэффициент
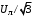 , где
, где 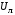 (кВ) – действующее значение междуфазного (линейного) базисного напряжения соответствующей ступени трансформации.
(кВ) – действующее значение междуфазного (линейного) базисного напряжения соответствующей ступени трансформации.При переходе через трансформатор симметричные составляющие напряжения прямой и обратной последовательностей изменяются не только по величине, но и по фазе в зависимости от группы (N) соединения его обмоток. Уравнения связи симметричных составляющих напряжений на выводах трансформатора с соединением обмоток звезда-треугольник в системе относительных единиц запишутся так:
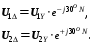
При этом имеется в виду, что
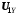 ,
, 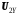 включают падение напряжения в трансформаторе, т.е.
включают падение напряжения в трансформаторе, т.е. 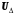 и
и 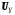 соответствуют одному и тому же узлу схемы.
соответствуют одному и тому же узлу схемы.Уравнения (3) справедливы и при переходе со стороны треугольника на сторону звезды, при этом угловые смещения симметричных составляющих меняют свой знак на противоположный.
Исследование режимов КЗ в настоящей работе ведется на основе схемы (рис. 1), в которой последовательно соединены генератор, трансформатор и высоковольтная ЛЭП.
Исходные данные
Таблица 1 – Исходные данные
| № вар. | 10 |
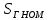 , МВА , МВА | 77,5 |
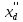 , о.е. , о.е. | 0,28 |
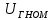 , кВ , кВ | 13,8 |
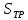 , МВА , МВА | 100 |
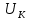 , % , % | 12 |
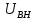 , кВ , кВ | 230 |
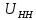 , кВ , кВ | 13,8 |
| L, км | 100 |
1. Построение эпюр распределения симметричных составляющих напряжения в о.е. для всех видов КЗ.
Принципиальная схема электропередачи представлена на рисунке 1. Эпюры распределения симметричных составляющих напряжения представлены на рисунках 2,3,4.
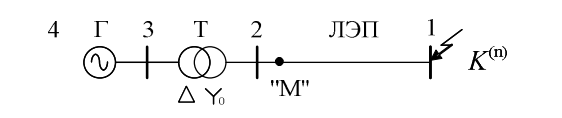
Рисунок 1 - Принципиальная схема электропередачи. 1, 2, 3, 4 - номера узлов схемы
Таблица 2 – Результаты расчета
| № | 1 | 2 | 3 | 4 |
| Двухфазное КЗ | ||||
| U1,о.е. | 0,550 | 0,625 | 0,743 | 1,100 |
| U2, о.е. | 0,550 | 0,475 | 0,357 | 0,000 |
| Двухфазное КЗ на землю | ||||
| U1, о.е. | 0,305 | 0,413 | 0,584 | 1,100 |
| U2, о.е. | 0,305 | 0,264 | 0,198 | 0,000 |
| U0, о.е. | 0,305 | 0,106 | 0,000 | - |
| Однофазное КЗ | ||||
| U1, о.е. | 0,681 | 0,738 | 0,828 | 1,100 |
| U2, о.е. | -0,419 | -0,362 | -0,272 | 0,000 |
| U0, о.е. | -0,261 | -0,090 | 0,000 | - |
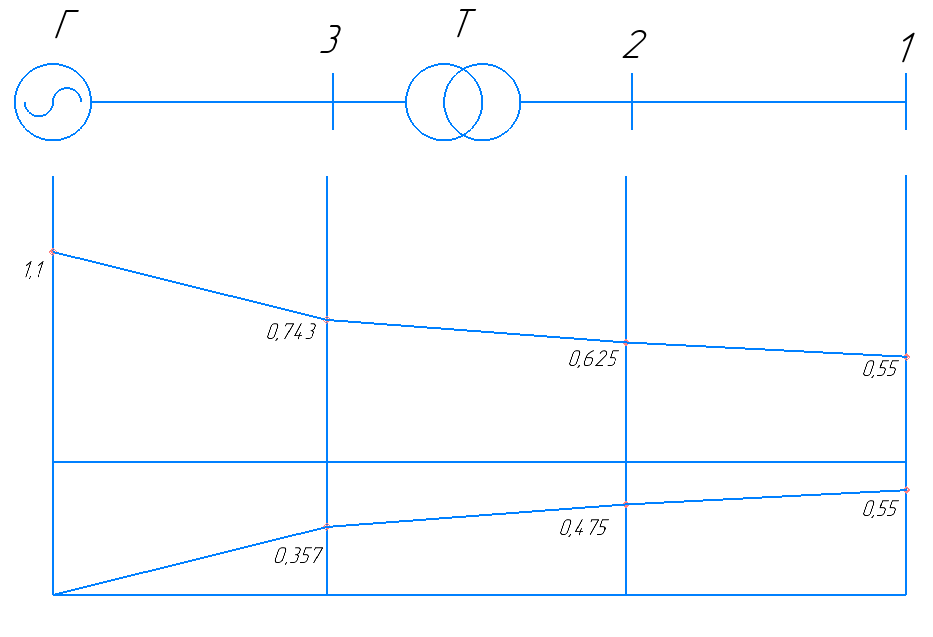
Рисунок 2 – Эпюры распределения симметричных составляющих напряжения для двухфазного КЗ
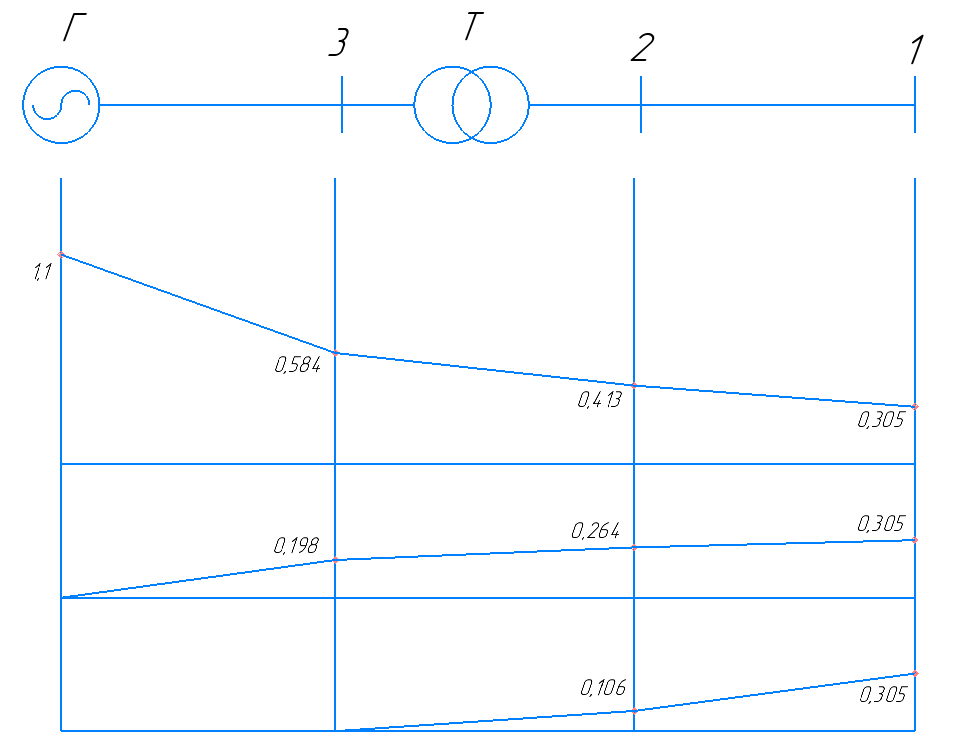
Рисунок 3 – Эпюры распределения симметричных составляющих напряжения для двухфазного КЗ на землю
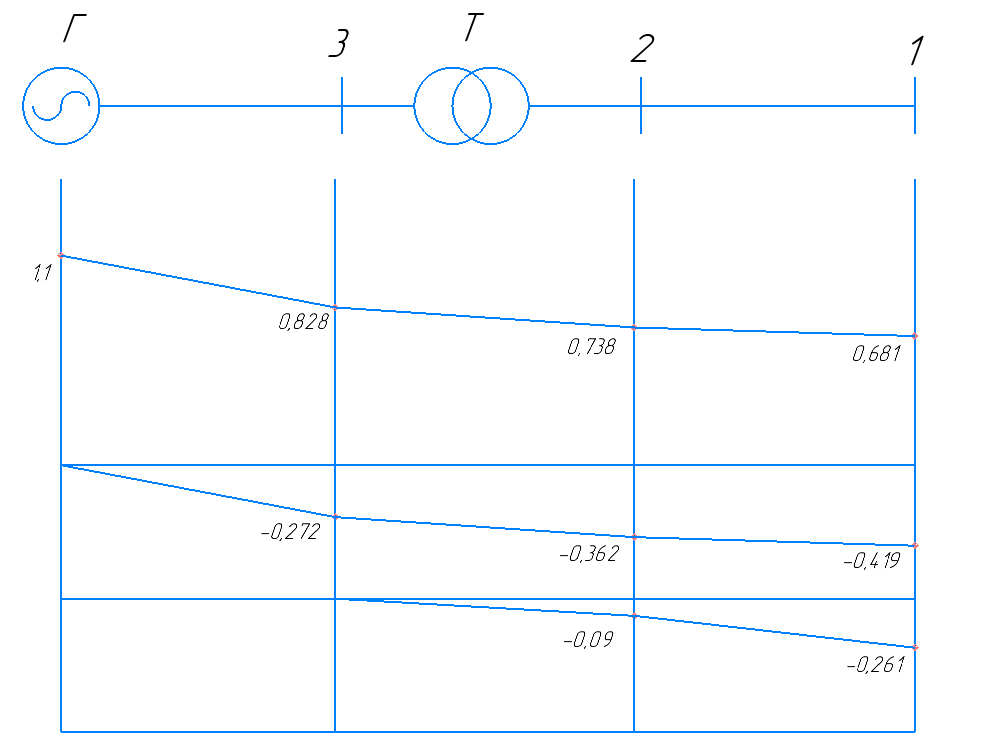
Рисунок 4 – Эпюры распределения симметричных составляющих напряжения для однофазного КЗ
2. Расчет симметричных составляющих напряжений в относительных и именованных единицах для точки М.
Схема замещения представлена на рисунке 5.
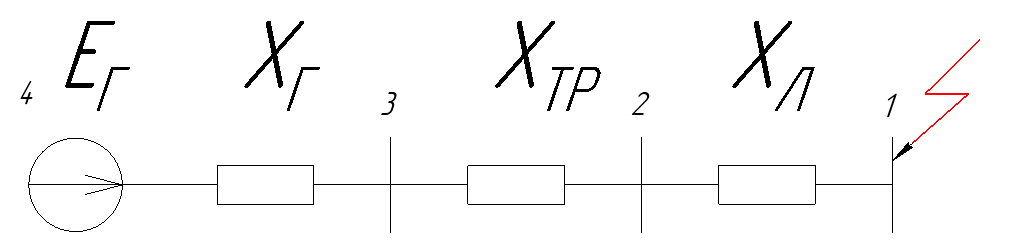
Рисунок 5 – Схема замещения
При расчетах режимов КЗ принимаем следующие условия по параметрам схемы:
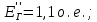
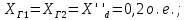
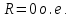
X1(L) = 0,4 Ом/км – погонная реактивность ЛЭП в схеме прямой последовательности;
X0(L) = 3X1(L) – погонная реактивность ЛЭП в схеме нулевой последовательности;
Расчет осуществляется аналитическим методом в системе относительных единиц, в качестве «особой» фазы принимаем фазу «А».
Параметры схемы замещения:
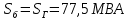
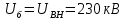
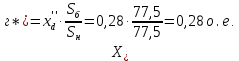
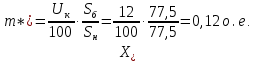
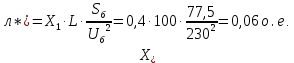
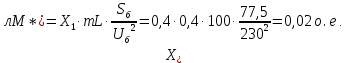
Прямая последовательность:
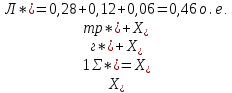
Обратная последовательность:
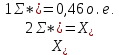
Нулевая последовательность:
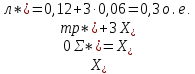
Граничные условия однофазного КЗ:
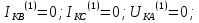
Эти условия дают соотношения между симметричных составляющими напряжения:
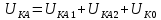
Определение симметричных составляющих тока и напряжения в фазе А:
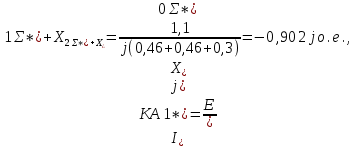
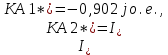
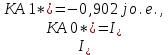
Нахождение симметричных составляющих напряжений для точки КЗ:
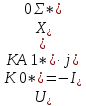
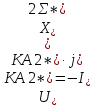
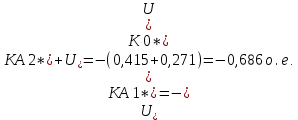
Расчет симметричных составляющих напряжений для точки М ЛЭП:
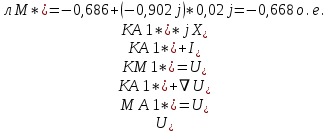
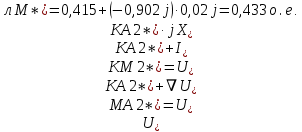
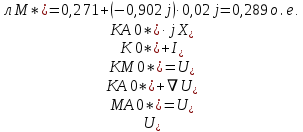
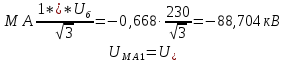
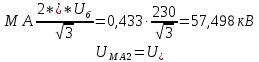
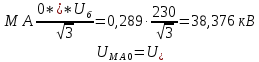
3. Построение векторных диаграмм напряжений для точки M.
Фаза А:
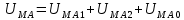
Фаза В:
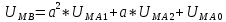
Фаза С:
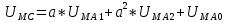
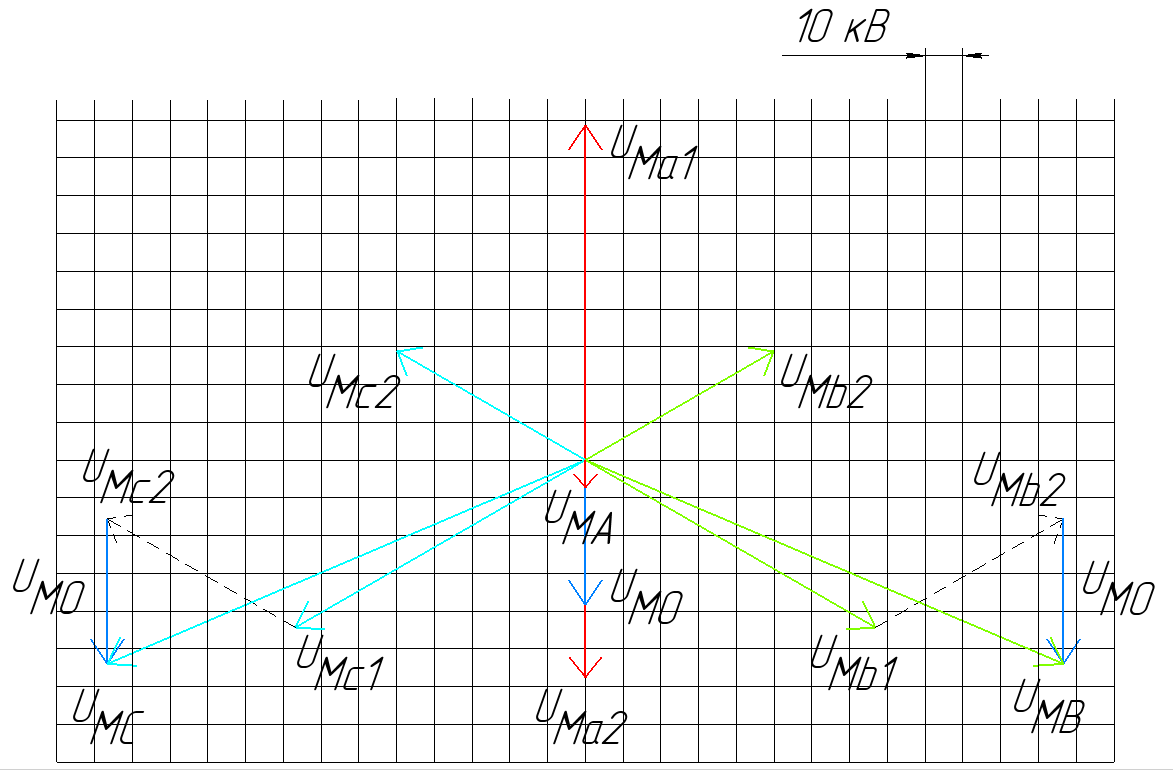 Рисунок 6 - Векторная диаграмма напряжений для точки M
Рисунок 6 - Векторная диаграмма напряжений для точки M4. Определение фазы симметричных составляющих напряжений с учетом группы соединения обмоток трансформатора для узла 3.