Федеральное агентство связи

ФГБОУ ВО «СибГУТИ»
Кафедра физики

Лабораторная работа 4.1

ОПРЕДЕЛЕНИЕ УДЕЛЬНОГО ЗАРЯДА ЭЛЕКТРОНА МЕТОДОМ МАГНЕТРОНА

Выполнил студент группы:
РИ-11 Труфанов Дмитрий Викторович

Проверил преподаватель:
Власов Александр Александрович

Измерения сняты
	Дата, подпись преподавателя
Отчет принят
	Оценка, дата, подпись преподавателя
Работа зачтена
	Оценка, дата, подпись преподавателя

1.ЦЕЛЬРАБОТЫ

1. 
   Ознакомиться с законами движения заряженных частиц в электрическом и магнитном полях.
   
2. 
   Определить удельный заряд электрона с помощью цилиндрического магнетрона.
   

2. 
   ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
   

Магнетроном называется электровакуумное устройство, в котором движениеэлектронов происходит во взаимно перпендикулярных электрическом имагнитном полях. Одно из применений магнетрона в том, что он являетсяисточником электромагнитного излучения СВЧ диапазона: ƒ10⁹÷10¹²ГцМагнетрон является основным элементом СВЧ печей (микроволновых печей),магнетроны широко используют в современных радиолокационных станциях. Внашей работе магнетрон имеет самую простую конструкцию и представляетсобой радиолампу-диод прямого накала, электродами которой являютсякоаксиальные цилиндры. Катодом является спираль по оси радиолампы, аанодом - цилиндр вокруг катода, с максимальной эффективностью собирающийэмитированные с катода электроны (рис.1). Радиолампа помещена во внешнееаксиальное магнитное поле, создаваемое соленоидом с током (Образец такогоустройства

---

приведенна рис. 2). Схематическое изображение устройства магнетрона (продольное сечение)представлено на рис.3. При этом силовые линии электрического поля имеютрадиальное направление, а линии индукции магнитного поля совпадают с осьюэлектродов.Нарис.4показанопоперечноесечениерадиолампысуказанием→направленийвекторовмагнитнойиндукцииBинапряженностиэлектрического→поляEПринагреваниикатодалампысегоповерхностиначинаютвылетатьэлектроны. Это явление называется термоэлектронной эмиссией.Эмитированные электроны движутся к аноду во взаимноперпендикулярныхэлектрическом и магнитном полях (рис.4). Электрическое поле создается междукатодом и анодом магнетрона источником анодного напряжения, а магнитноеполе – соленоидом (цилиндрической катушкой) с током, внутри которого инаходится вакуумный диод. Таким образом, электроны могут двигаться внутрицилиндрическогообъёма,ограниченногоанодомэлектроннойлампы.По второму закону Ньютона движение электрона в скрещенных электрическомимагнитномполяхможет быть описано: → → _→→ma= qE+ q_[υB_]В нашем случае m — масса электрона, q= – e, где е — абсолютная величиназаряда электрона, υ — скорость электрона. В правой части уравнения (1)записана сила, состоящая из двух слагаемых: силы Кулона, действующей состороны электрического поля и направленной вдоль силовых линий, и

---

магнитнойсилыЛоренца,действующейсосторонымагнитногополянадвижущийся заряд и направленной перпендикулярно траектории движенияэлектрона. Направление силы Лоренца определяются по правилу «левой руки»для положительного заряда. Траектория движения заряженной частицы вэлектромагнитном поле существенно зависит от величины удельного заряда —отношения зарядачастицы к её массе. Вид траектории может быть получен изрешения уравнения (1), но даже в случае цилиндрической симметрии этоуравнение не имеет решения в аналитическом виде. Рассмотрим накачественном уровне движение электрона в цилиндрическом магнетроне. Дляупрощения предположим, что электроны вылетают из катода с нулевойначальной скоростью, движение происходит в плоскости, перпендикулярнойоси электродов, т. е. в плоскости рис.2, и что радиус катода существенноменьше радиуса анода. При протекании тока в цепи накала в результатетермоэлектронной эмиссии вокруг катода в лампе образуются свободныеэлектроны.Вэлектрическомполе,обусловленноманоднымнапряжениемU_a , , эти электроны двигаются от катода к аноду, что может бытьзафиксировано по анодному току лампы. Постоянный ток в обмотке соленоидасоздаетмагнитноеполе,искривляющеетраекториюдвиженияэлектронов.Выяснимхарактердвиженияэлектроноввэлектрическомимагнитномполях.В

---

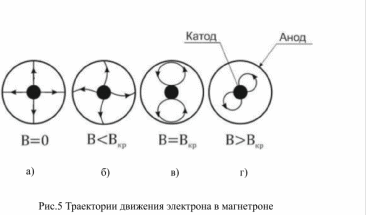В магнетроне электрон движется в скрещенных электрическом и магнитномполях. В отсутствии магнитного поля траектория движения приведена нарис.5а. При наложении «слабого» магнитного поля траектория электроновискривляется, но, тем не менее, все электроны долетают до анода (рис. 5б).Увеличивая индукцию магнитного поля, можно получить ситуацию, когдаэлектрон, двигаясь по криволинейной траектории, едва не коснется анода ивозвратится на катод (рис. 5в). Криволинейная траектория в этом случаепредставляетсобойокружность,радиускоторойдляэлектронавблизианода 2примерно равен половине радиуса анода двухэлектродной лампы R= ₍^Ra₎Используя формулу (4) можно переписать выражение для радиуса траекторииэлектронав этомслучае:

---

=^Ramυ2 eBАнодныйтокприэтомпрекращается.Таким образом, если известна индукция критического магнитного поля приопределенном анодном напряжении, то из формул (2) и (5) можно рассчитатьудельныйзаряд электрона: =_e8·U_a^m R²·B^2a кр 2При дальнейшем увеличении магнитного поля электроны, двигаясь по криволинейным замкнутым траекториям, удаляются от катода на меньшие расстояния и никогда не долетают до анода (рис. 5г). В этом случае, когда

---

Смотрите также файлы

• Ведомост ь учета результатов вождения упражнения.docx

• Практическая работа 2 Построение диаграммы контрольных событий. Диаграмма Ганта.pdf

• День до сдачи работы мы справимся, и ты получишь Отлично по своему предмету! Только представь ты занимаешься своим любимым делом, пока твои лохиодногруппники теряют свои нервные клетки Проникнись Это бесценное ощущение Курсовая,.docx

• 1. Что такое электромагнитные волны.ppt

• Банкир ос сия всем бедам назло вопросы кб ан ко в с кой системе наго д.pdf