Файл: 1 2 Земной эллипсоид и его основные элементы. Общий земной эллипсоид и референцэллипсоид, требования к ним. Уровенные поверхности и их свойства..doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 12.01.2024
Просмотров: 94
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
М, будет перпендикулярно меридианному сечению точки М.
Обозначим через M и N радиусы кривизны меридиана и первого вертикала. Не приводя выводы формул, запишем:
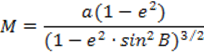
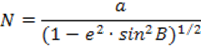
, где: a – большая полуось эллипсоида; e – первый эксцентриситет эллипсоида; B – геодезическая широта точки M.
Из формул видно, что радиусы кривизны возрастают при увеличении широты. Запишем отношение N и M.
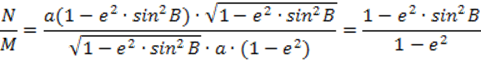
Н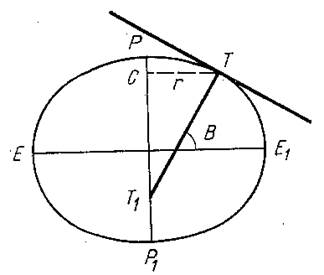
а полюсе B=90˚, поэтому на полюсе M и N будут равны. Во всех остальных случаях N больше M. Если меридиан имеет меньший радиус, то кривизна наибольшая. Радиусом кривизны первого вертикала является отрезок нормали ТТ1.
Средним радиусом кривизны в данной точке поверхности называется предел, к которому стремится среднее арифметическое из радиусов кривизны нормальных сечений, когда число их стремится к бесконечности.
Для точек эллипсоида средний радиус кривизны Rравен среднему геометрическому из радиусов кривизны главных нормальных сечений, меридиана и первого вертикала, проведенных для той же точки.
Радиус кривизны меридиана применяют при вычислении длин дуг меридианов и разности широт.
Разность кривизны первого вертикала применяют при вычислении длин дуг параллелей, разности долгот и азимутов.
Средний радиус кривизны применяют, когда Землю принимают за шар; при вычислении сферических избытков и других случаях.
Если TT1 радиус кривизны первого вертикала, а r – радиус кривизны параллели, проходящей через точку T, то
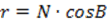
Вычисление длин дуг меридианов и параллелей.
Пусть требуется определить длину дуги меридиана между точками A и C с широтами B1 и B2. Разобьем этот отрезок дуги на бесконечно малые отрезки
, тогда дуга малого отрезка выразится формулой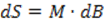
, как малый отрезок дуги окружности радиуса M.
Д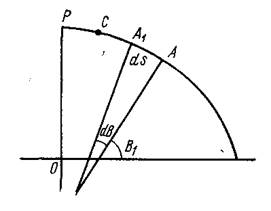
лина всей дуги Ac определится из интегрирования функции 
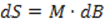в пределах от B1 до B2:
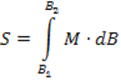
В триангуляции, при длинах дуг свыше 45 км используется формула:
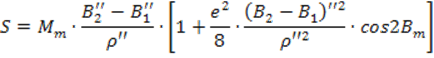
Здесь: Mm – радиус кривизны меридиана для средней широты
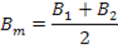
Для длин дуг менее 45 км можно воспользоваться формулой:
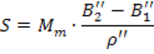
,это означает, что длину дуги можно определить, как дугу центрального угла окружности равном B2-B1.
Длина дуги параллели (окружности) определяется формулой:
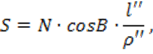
, где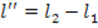
.
Понятие о взаимных нормальных сечениях и геодезической линии.
Возьмем на поверхности эллипсоида две точки A и B, не лежащие на одном меридиане с широтами BA и BС. Широта BС >BA. Проведем нормали в точках A и B. Нормали не пересекаются, так как лежат в разных плоскостях. Широты BA и BСне равны, значит нормали пересекают малую ось эллипсоида в разных местах. Нормаль с более северной широтой пересекает малую ось южнее, чем нормаль с меньшей широтой.
П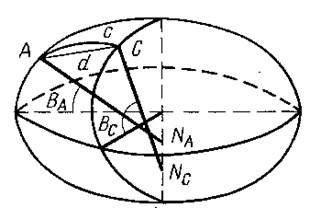
лоскость, проходящая через нормаль ANA и точку C, не совпадает с плоскостью, проведенной через нормаль CNC и точку A. Первая плоскость образует с поверхностью эллипсоида нормальное сечение
AAC, вторая нормальное сечение CCA. Между двумя точками поверхности эллипсоида проходят два нормальных сечения, которые называются взаимными нормальными сечениями. Сечение AAC прямое, а сечение CCA обратное в точке A.
Если начальная точка A лежит южнее точки C, то прямое нормальное сечение точки A отклоняется к югу от обратного.
Прямое нормальное сечение можно представить, если в точке A установить теодолит, чтобы его вертикальная ось совпадала с нормалью, то при визировании на вторую точку C, выставленные в створе вешки, обозначат прямое нормальное сечение на поверхности эллипсоида.
При измерении на земной поверхности вертикальная ось теодолита устанавливается по отвесной линии, в то время как прямое нормальное сечение является стороной триангуляции, полигонометрии на поверхности эллипсоида. Значит, при проектировании на поверхность эллипсоида надо вводить поправки за уклонение отвесных линий и за высоту наблюдаемой цели над поверхностью эллипсоида.
В равнинных районах принимают измеренные направления на поверхности Земли такими же и на поверхности эллипсоида. Если по измеренным направлениям составить треугольники, то стороны следует изобразить взаимно обратными нормальными сечениями. Значит, на поверхности эллипсоида не образуется замкнутой фигуры.
В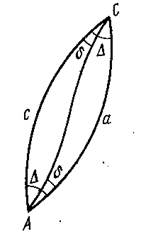
еличина угла Δ между взаимными нормальными сечениями небольшая и зависит от длины линии S, ее азимута A и широты B. Так при B=60˚, A=50˚ при:
· S=30 км Δ=0,004"
· S=100 км Δ=0,032"
При положении пунктов на одном меридиане или на одной параллели взаимные нормальные сечения сливаются в одну линию.
В триангуляции 2,3,4 класса двойственностью нормальных сечений пренебрегают.
В триангуляции 1 класса двойственность нормальных сечений устраняют тем, что пункты соединяют геодезическими линиями. Геодезическая линия – это кривая, являющаяся кратчайшим расстоянием между двумя точками на поверхности эллипсоида.
Геодезическая линия в точках A и C располагается к прямым нормальным сечениям и составляет с ним угол δ равный 1/3 Δ.
Обозначим через M и N радиусы кривизны меридиана и первого вертикала. Не приводя выводы формул, запишем:
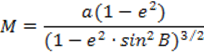
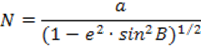
, где: a – большая полуось эллипсоида; e – первый эксцентриситет эллипсоида; B – геодезическая широта точки M.
Из формул видно, что радиусы кривизны возрастают при увеличении широты. Запишем отношение N и M.
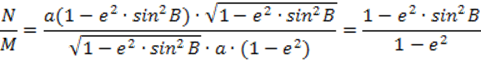
Н
а полюсе B=90˚, поэтому на полюсе M и N будут равны. Во всех остальных случаях N больше M. Если меридиан имеет меньший радиус, то кривизна наибольшая. Радиусом кривизны первого вертикала является отрезок нормали ТТ1.Средним радиусом кривизны в данной точке поверхности называется предел, к которому стремится среднее арифметическое из радиусов кривизны нормальных сечений, когда число их стремится к бесконечности.
Для точек эллипсоида средний радиус кривизны Rравен среднему геометрическому из радиусов кривизны главных нормальных сечений, меридиана и первого вертикала, проведенных для той же точки.
Радиус кривизны меридиана применяют при вычислении длин дуг меридианов и разности широт.
Разность кривизны первого вертикала применяют при вычислении длин дуг параллелей, разности долгот и азимутов.
Средний радиус кривизны применяют, когда Землю принимают за шар; при вычислении сферических избытков и других случаях.
Если TT1 радиус кривизны первого вертикала, а r – радиус кривизны параллели, проходящей через точку T, то
Вычисление длин дуг меридианов и параллелей.
Пусть требуется определить длину дуги меридиана между точками A и C с широтами B1 и B2. Разобьем этот отрезок дуги на бесконечно малые отрезки
, тогда дуга малого отрезка выразится формулой
, как малый отрезок дуги окружности радиуса M.Д
лина всей дуги Ac определится из интегрирования функции 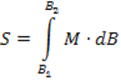в пределах от B1 до B2: В триангуляции, при длинах дуг свыше 45 км используется формула:
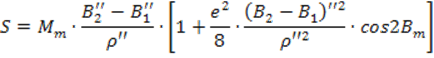
Здесь: Mm – радиус кривизны меридиана для средней широты
Для длин дуг менее 45 км можно воспользоваться формулой:
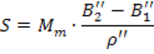
,это означает, что длину дуги можно определить, как дугу центрального угла окружности равном B2-B1.
Длина дуги параллели (окружности) определяется формулой:
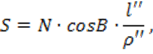
, где
.Понятие о взаимных нормальных сечениях и геодезической линии.
Возьмем на поверхности эллипсоида две точки A и B, не лежащие на одном меридиане с широтами BA и BС. Широта BС >BA. Проведем нормали в точках A и B. Нормали не пересекаются, так как лежат в разных плоскостях. Широты BA и BСне равны, значит нормали пересекают малую ось эллипсоида в разных местах. Нормаль с более северной широтой пересекает малую ось южнее, чем нормаль с меньшей широтой.
П
лоскость, проходящая через нормаль ANA и точку C, не совпадает с плоскостью, проведенной через нормаль CNC и точку A. Первая плоскость образует с поверхностью эллипсоида нормальное сечение
AAC, вторая нормальное сечение CCA. Между двумя точками поверхности эллипсоида проходят два нормальных сечения, которые называются взаимными нормальными сечениями. Сечение AAC прямое, а сечение CCA обратное в точке A.
Если начальная точка A лежит южнее точки C, то прямое нормальное сечение точки A отклоняется к югу от обратного.
Прямое нормальное сечение можно представить, если в точке A установить теодолит, чтобы его вертикальная ось совпадала с нормалью, то при визировании на вторую точку C, выставленные в створе вешки, обозначат прямое нормальное сечение на поверхности эллипсоида.
При измерении на земной поверхности вертикальная ось теодолита устанавливается по отвесной линии, в то время как прямое нормальное сечение является стороной триангуляции, полигонометрии на поверхности эллипсоида. Значит, при проектировании на поверхность эллипсоида надо вводить поправки за уклонение отвесных линий и за высоту наблюдаемой цели над поверхностью эллипсоида.
В равнинных районах принимают измеренные направления на поверхности Земли такими же и на поверхности эллипсоида. Если по измеренным направлениям составить треугольники, то стороны следует изобразить взаимно обратными нормальными сечениями. Значит, на поверхности эллипсоида не образуется замкнутой фигуры.
В
еличина угла Δ между взаимными нормальными сечениями небольшая и зависит от длины линии S, ее азимута A и широты B. Так при B=60˚, A=50˚ при: · S=30 км Δ=0,004"
· S=100 км Δ=0,032"
При положении пунктов на одном меридиане или на одной параллели взаимные нормальные сечения сливаются в одну линию.
В триангуляции 2,3,4 класса двойственностью нормальных сечений пренебрегают.
В триангуляции 1 класса двойственность нормальных сечений устраняют тем, что пункты соединяют геодезическими линиями. Геодезическая линия – это кривая, являющаяся кратчайшим расстоянием между двумя точками на поверхности эллипсоида.
Геодезическая линия в точках A и C располагается к прямым нормальным сечениям и составляет с ним угол δ равный 1/3 Δ.