Файл: Контрольная работа 1. Элементы линейной алгебры, векторной алгебры, аналитической геометрии и математического анализа. Задание 1.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 12.01.2024

Просмотров: 57

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


С осью Оу: .

Точка - точка пересечения с осью Оу.

  1. Находим производную.



при .

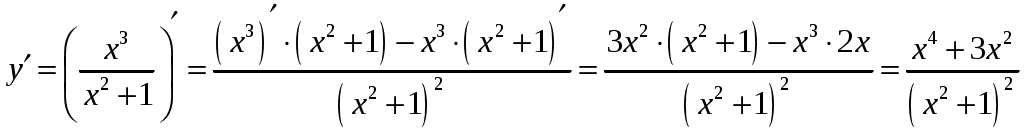
Критическая точка: .




+ +




0

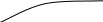
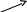
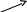
Функция возрастает на всей области определения, т.к. .

  1. Находим вторую производную.


при , и .
+ – + –



0

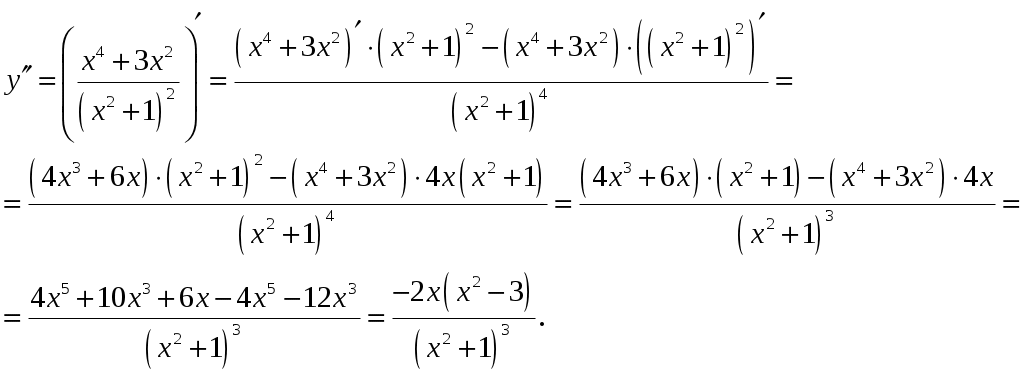
Функция выпукла на интервалах , функция вогнута на интервале .

Находим точки перегиба и значения функции в этих точках:







  1. Так как точек разрыва нет, то вертикальных асимптот нет.

Найдем наклонные асимптоты

Вычисляем пределы:





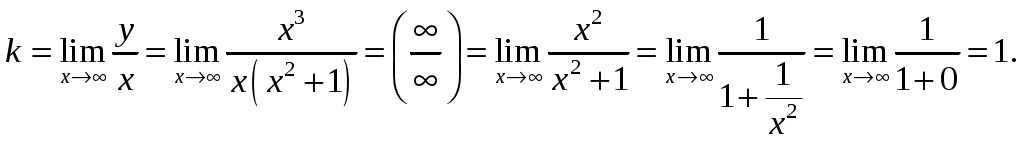
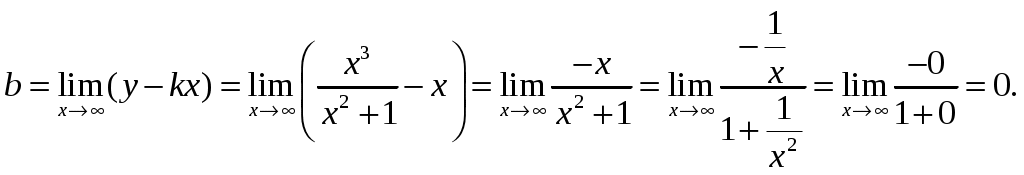
Тогда - наклонная асимптота графика функции.

  1. По полученным данным строим график функции.



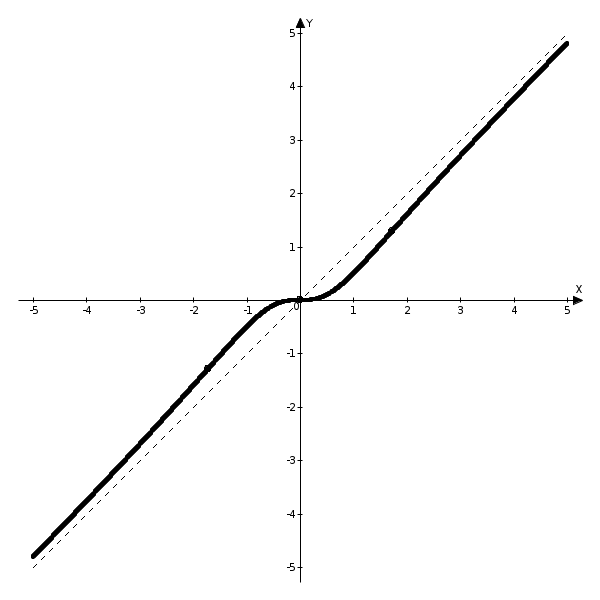
Задание 4.

8.2.61–8.2.70. Вычислить площадь фигуры, ограниченной заданными

линиями. Сделать чертеж.

8.2.65. .

Решение.

Построим фигуру.



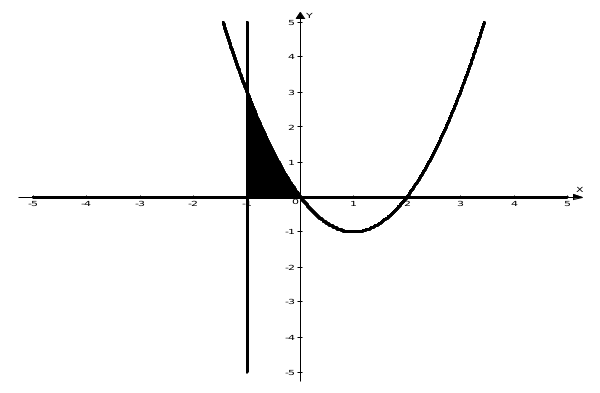
Пределы интегрирования заданы это и . Линии, ограничивающие сверху
данную фигуру и снизу . Найдем площадь фигуры по формуле



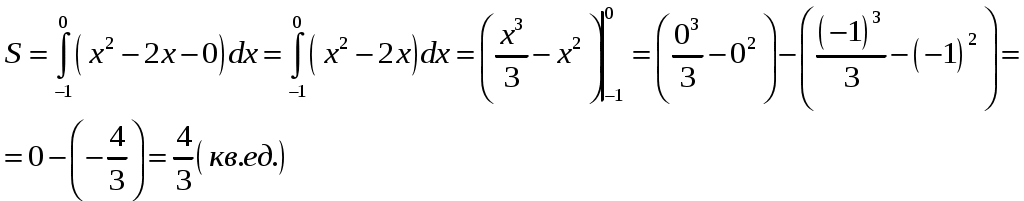
Ответ: .

Задание 5.

9.2.21-9.2.30. Найти стационарные точки функции F(x, y) и исследовать их на локальный экстремум.

9.2.25.

Решение.

Найдем частные производные данной функции:

;

.

Для нахождения точек экстремума, применим необходимое условие локального экстремума дифференцируемой функции:



Получаем:



Точка – точка экстремума.

Находим выражения:



Определяем характер точки экстремума:

В точке :

Тогда

Так как и
то в точке экстремум минимум.

Тогда

.

Ответ: .

Смотрите также файлы