Файл: 2 Сложное движение точки и твердого тела.docx

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯРОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждениевысшего образования«Тольяттинский государственный университет»Институт инженерной и экологической безопасности(наименование института полностью)Кафедра /департамент /центр___________________________(наименование кафедры/департамента/центраполностью) 20.03.01 Техносферная безопасность________(код и наименование направления подготовки, специальности)практическое ЗАДАНИЕ №_6__по учебному курсу ___Механика 1_____(наименование учебного курса)Вариант ___ (при наличии)Студент Группа

• 
  Преподаватель
  

Тольятти 2023 год.

Практическое задание 6

Тема 2.5. Сложное движение точки и твердого телаЗаданиеКруглая пластина (рис. 6.1) радиусом 0,1(С + 1) (м) вращается вокруг неподвижной оси, проходящей перпендикулярно рисунку через нижнюю точку О по закону Пt² – Гt (рад). По окружности пластины движется точка М из точки А. Закон ее относительного движения – длина дуги между точками А и М равна 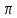(П + 1)t² (м). Определите абсолютную скорость и ускорение точки М в момент времени 1 с.Рис. 6.1РешениеВыполним рисунок 6.2, на котором покажем точку, совершающую сложное движение на теле, в заданный момент времени.Найдем все скорости точки.Определим положение точки на пластине при t = 1 c.S = 9π·1² = 28,3

---

м.Угол между радиусами:а = S/R = 28,3/0,8 = 35,4 рад или а = 2030,3° → а = 230,3°Так как точка участвует в нескольких движениях, то следует определить ее составные движения.1.Относительным движением точки является движение по окружности по заданному закону S(t) = 9πt².2.Переносным движением точки является вращение вместе с пластиной вокруг оси.3.Абсолютным движением точки М будет сложное движение по некоторой кривой. Известно, что 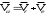. 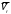= dS/dt = 18πt. При t = 1 c. 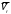= 18π·1 = 56,5 м/с.Вектор 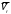направлен по касательной к окружности. 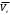= ωR_e.R_e определяем по теореме косинусов:R_e² = R² + R² - 2R²cos50,3° = 0,8² + 0,8² - 2·0,8²·0,639 = 0,462R_e = 0,68 мφ = 8t² – 6tω = dφ/dt = 16t – 6; при t = 1 с. ω = 10 с^-1. 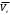= 10·0,68 = 6,8 м/с.С точкой связываем систему координат xy и на эти оси проецируем векторное равенство для Vв развернутом виде:V_x = - V_r·cos50,3º - V_e·cos64,9º = -56,5·0,639 – 6,8·0,424 = 40,0 м/с. V_y = V_r·sin50,3º -V_e·sin64,9º = 56,5·0,769 - 6,8·0,906 = 37,3 м/с. V = (V_х² + V_у²)^1/2 = (40² + 37,3²)^1/2 = 54,7 м/с.Определим направление вектора V:cos(V;i) = V_x/V = 40/54,7 = 0,731; 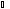(V;i) = 43,0º. cos(V;j) = V_y/V = 37,3/54,7 = 0,682; 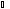(V;j) = 47,0º. Найдем все ускорения точки.Абсолютное ускорение точки М определится по формуле:

---

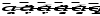
Вектор 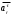направлен по касательной. 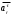= dV_r/dt = 18π. При t = 1 c. 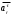= 18π = 56,5 м/с². Вектор 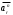направлен по радиусу R к центру окружности: 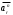= V_r²/R = 56,5²/0,8 = 3990 м/с².Вектор 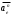направлен по радиусу R_e к оси вращения: 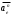= ω²R_e = 10²·0,68 = 68 м/с². 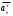= εR_e.ε = dω/dt = 16 c^-2 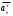= εR_e = 16·0,68 = 10,9 м/с². 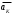= 2ωV_rsin(ω;V_r)Так как ω направлен по оси вращения, а V_r лежит в плоскости пластины, то: (ω;V_r) = 90º.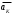 = 2·10·56,5·1 = 1130 м/с².Для определения направления вектора 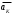применим правило Жуковского. Вектор V_r проецируем на плоскость, перпендикулярную оси переносного вращения, затем полученную проекцию поворачиваем на угол 90º в сторону переносного вращения. С точкой связываем систему координат ху и на эти оси проецируем векторное равенство для а в развернутом виде:а_x= - а_r^τ·cos50,3º - а_е^τ·cos64,9º + а_еⁿ·cos25,2º + а_rⁿ·cos39,7º - а_K·cos

---

39,7º = = -56,5·0,639 – 10,9·0,424 + 68·0,905 + 3990·0,769 - 1130·0,769 = 2220 м/с². а_y = а_r^τ·sin50,3º - а_е^τ·sin64,9º - а_еⁿ·sin25,2º + а_rⁿ·sin39,7º - а_K·sin39,7º = = 56,5·0,769 – 10,9·0,906 - 68·0,426 + 3990·0,639 - 1130·0,639 = 1832 м/с². а = (а_х² + а_у²)^1/2 = (2220² + 1832²)^1/2 = 2878 м/с².Определим направление вектора а:cos(а;i) = а_x/а = 2220/2878 = 0,771; (а;i) = 39,6º. cos(а;j) = а_y/а = 1832/2878 = 0,637; (а;j) = 50,4º.На рисунке покажем все векторы скоростей (рис. 6.2) и ускорений точки (рис. 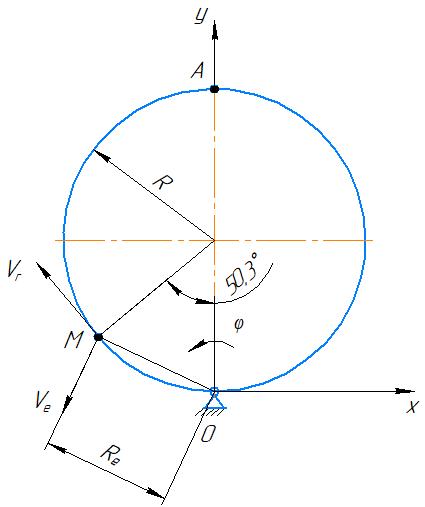6.3).Рис. 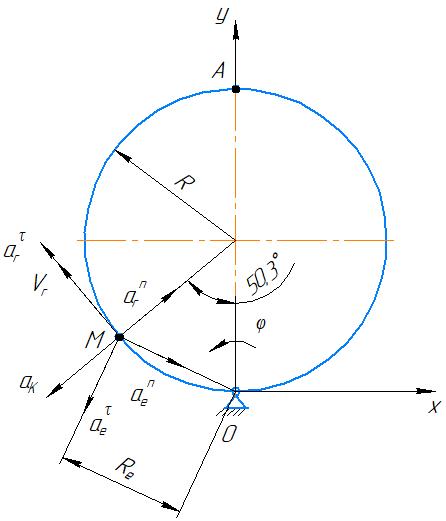6.2Рис. 6.3Ответ:V = 54,7 м/с; а = 2878 м/с².

---