МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное автономное образовательное учреждение высшего образования

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
АЭРОКОСМИЧЕСКОГО ПРИБОРОСТРОЕНИЯ»

КАФЕДРА № 52


ОТЧЕТ ЗАЩИЩЕН С ОЦЕНКОЙ__________________
ПРЕПОДАВАТЕЛЬ

Доцент, канд.техн.наук, доцент				Н.В. Марковская
должность, уч. степень, звание		подпись, дата		инициалы, фамилия

ОТЧЕТ О ЛАБОРАТОРНОЙ РАБОТЕ №3

ИССЛЕДОВАНИЕ ИНТЕНСИВНОСТИ ОТКАЗОВ ДЛЯ НЕВОССТАНАВЛИВАЕМЫХ СИСТЕМ

по курсу: НАДЕЖОСТЬ ИНФОКОММУНИКАЦИОННЫХ СИСТЕМ

СТУДЕНТ ГР. №		5922				К. Д. Камышников
	номер группы			подпись, дата		инициалы, фамилия

Санкт-Петербург

2022

1. 
   Цели работы:
   

• 
  Выбор периода жизни системы и соответствующей ему статистической модели;
  
• 
  Имитационное моделирование процесса функционирования невосстанавливаемой системы для выбранного периода жизни системы;
  
• 
  Построение зависимости ????̂(????) оценки интенсивности отказов от времени.
  

2. 
   Ход работы
   

Процесс функционирования невосстанавливаемой системы можно разделить на 3 периода:

---

1. 
   Период приработки
   

Время жизни системы:



– случайное число в интервале от 0 до 1.
Теоретическая функция надежности:



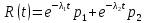
Теоретическая функция интенсивности отказа:



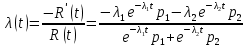
В результате моделирования системы получаем графики зависимости надежности и интенсивности отказов от времени функционирования системы (эти и последующие графики построены при входных данных: p₁ = 0.6; p₂ = 0.4; λ₁ = 0.7; λ₂ = 1.3).



Рис.1 Теоретический и практический графики функции надежности



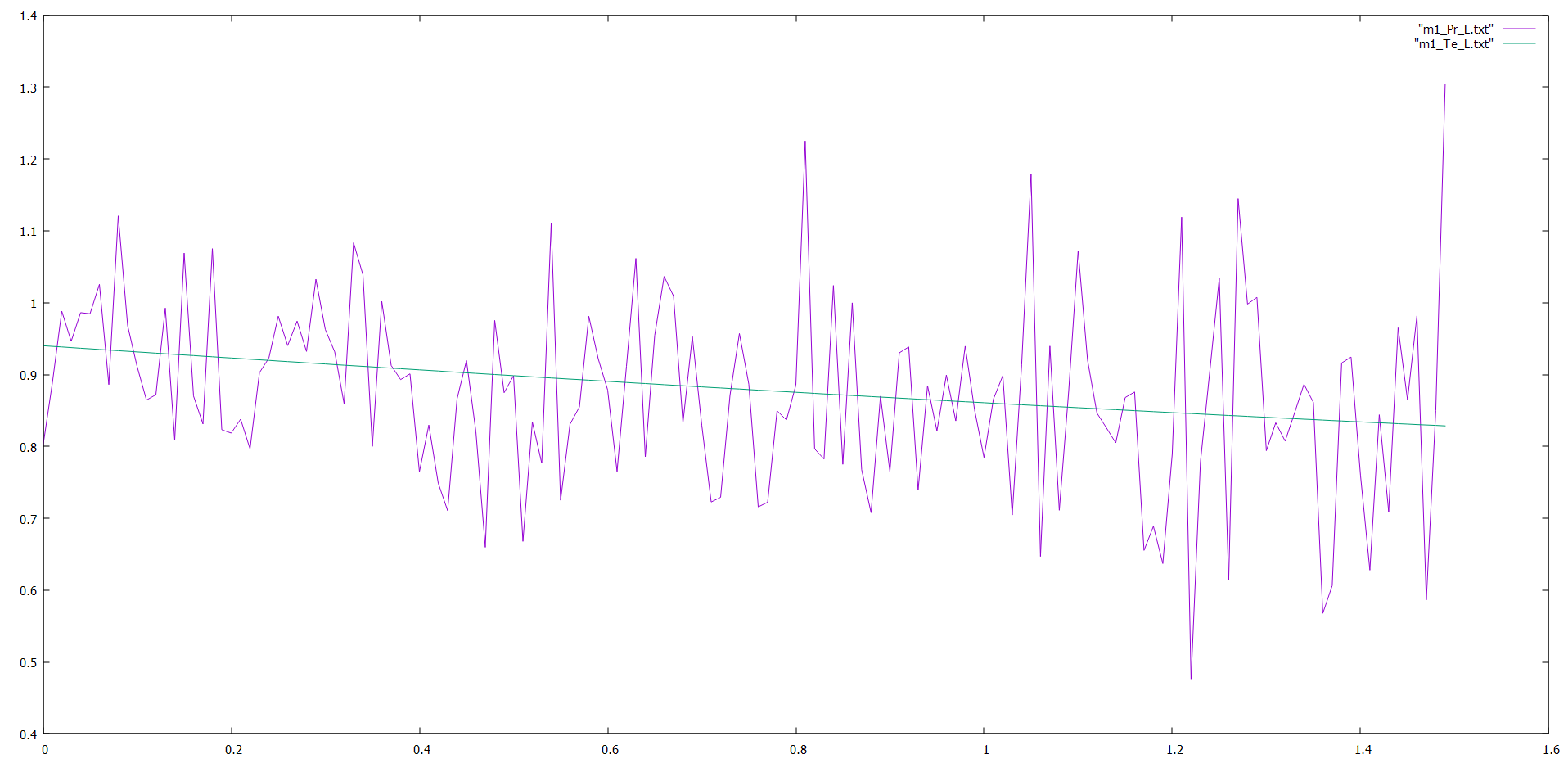
Рис.2 Теоретический и практический графики интенсивности отказов

2. 
   Период нормального функционирования
   

Время жизни системы:







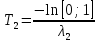
Теоретическая функция надежности:



Теоретическая функция интенсивности отказа:



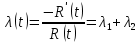
В результате моделирования системы получаем следующие графики:



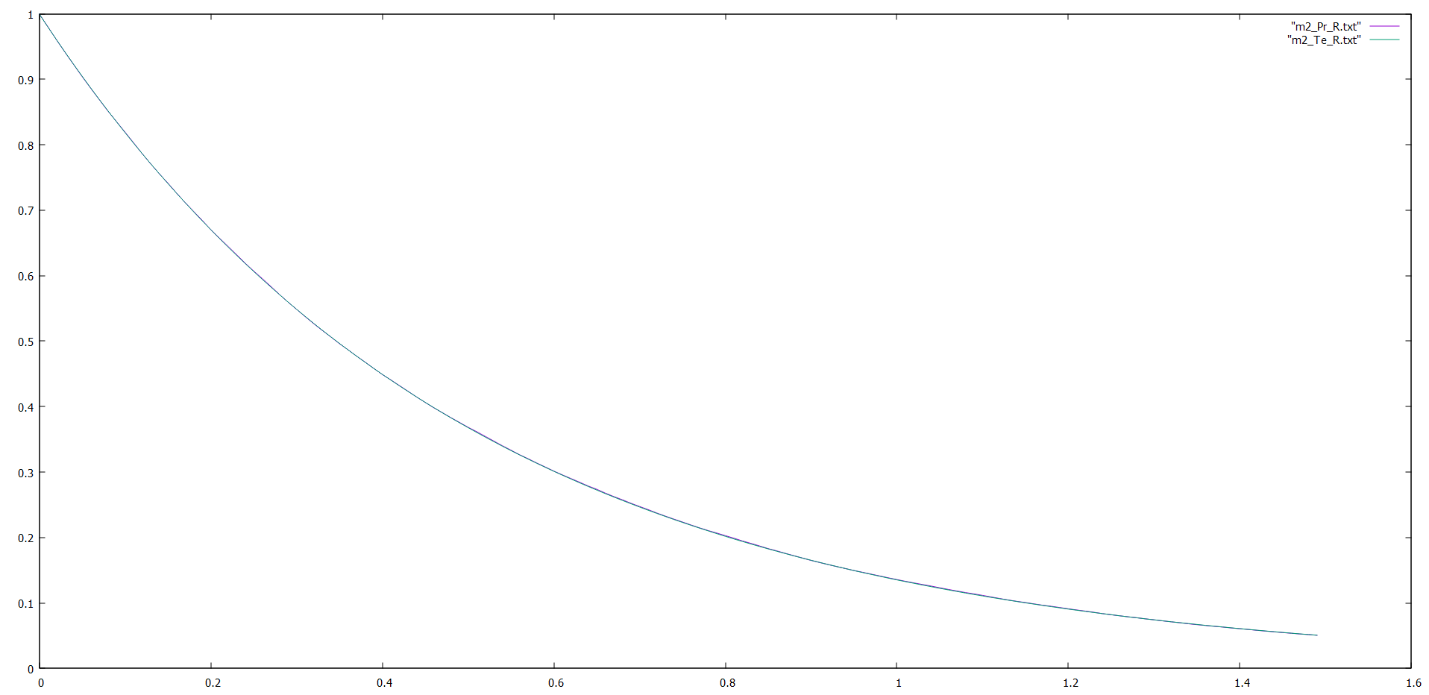
Рис.3 Теоретический и практический графики функции надежности



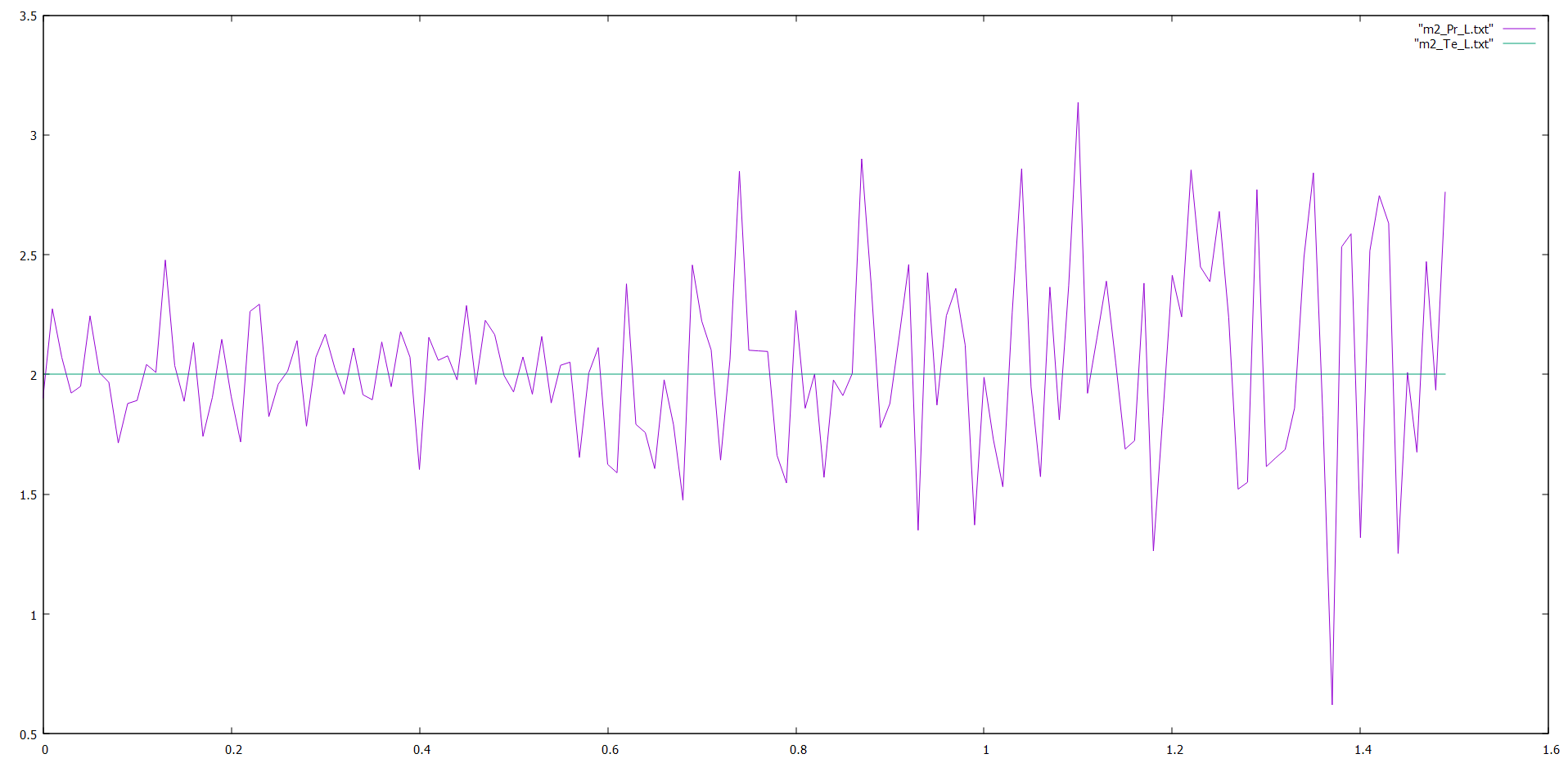
Рис.4 Теоретический и практический графики интенсивности отказов

3. 
   Период старения
   

Время жизни системы:

---

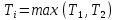
Теоретическая функция надежности:



Теоретическая функция интенсивности отказа:



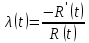
В результате моделирования системы получаем следующие графики:



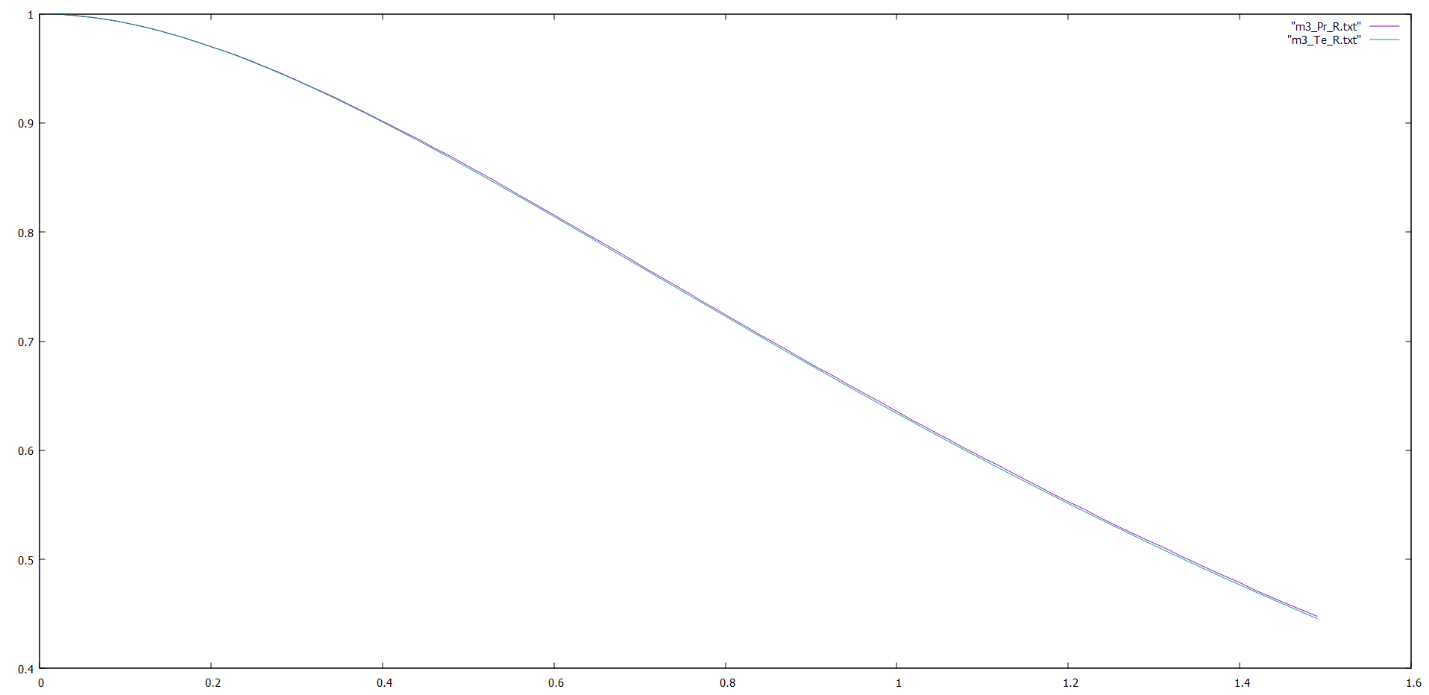
Рис.5 Теоретический и практический графики функции надежности



Рис.6 Теоретический и практический графики интенсивности отказов

3. 
   Вывод
   

В ходе лабораторной работы было реализовано имитационное моделирование процесса функционирования невосстанавливаемой системы для всех периодов жизни. Были построены графики зависимости надежности и интенсивности отказов от времени функционирования системы. Графики функции надежности не сильно отличаются друг от друга. Практические графики интенсивности отказов имеют колебательную форму, но если провести среднюю линию, то она будет схожа с теоретическим графиком. Таким образом, моделирование системы выполнено правильно.

4. 
   Листинг
   

Приложение 1

#include

#include

#include
using namespace std;
double p[] = { 0.6, 0.4 };

double lambda[] = { 0.7, 1.3 };

int N = 10000;
void write(string filename, vector Ti, int num)

{

vector R;

vector Lambda;

vector R_T;

vector Lambda_T;

int Nt = 0;

int Ntdt = 0;

fstream outR(filename + "_Pr_R.txt", ios::out);

fstream outL(filename + "_Pr_L.txt", ios::out);

for (double t = 0; t < 3; t += 0.01)

{

for (int i = 0; i < N; ++i)

{

if (Ti[i] >= t)

{

Nt++;

}

if (Ti[i] >= (t + 0.001))

{

Ntdt++;

}

}

R.push_back((double)Nt / (double)N);

Lambda.push_back(((double)Nt - (double)Ntdt) / ((double)Nt * 0.001));

outR << t << " " << R[R.size() - 1] << endl;

outL << t << " " << Lambda[Lambda.size() - 1] << endl;

Nt = 0;

Ntdt = 0;

}

outR.close();

outL.close();

outR.open(filename + "_Te_R.txt", ios::out);

outL.open(filename + "_Te_L.txt", ios::out);

for (double t = 0; t < 3; t += 0.01)

{

if (num == 1)

{

R_T.push_back(exp(-lambda[0] * t) * p[0] + exp(-lambda[1] * t) * p[1]);

Lambda_T.push_back(-((exp(-lambda[0] * t) * p[0] * (-lambda[0]) + exp(-lambda[1] * t) * p[1] * (-lambda[1])) / R_T[R_T.size() - 1]));

}

if (num == 2)

{

R_T.push_back(exp(-lambda[0] * t) * exp(-lambda[1] * t));

Lambda_T.push_back(lambda[0] + lambda[1]);

}

if (num == 3)

{

R_T.push_back(exp(-lambda[0] * t) + exp(-lambda[1] * t) - exp(-(lambda[0] + lambda[1]) * t));

Lambda_T.push_back(-(((-lambda[0] * exp(-lambda[0] * t)) - (lambda[1] * exp(-lambda[1] * t)) + (lambda[0] + lambda[1]) * exp(-(lambda[0] + lambda[1]) * t)) / (R_T[R_T.size() - 1])));

}

outR << t << " " << R_T[R_T.size() - 1] << endl;

outL << t << " " << Lambda_T[Lambda_T.size() - 1] << endl;

}

outR.close();

outL.close();

}
void model1()

{

vector Ti;

srand(time(0));

for (int i = 0; i < N; ++i)

{

double tmp = ((double)rand() + 1) / RAND_MAX;

if ((rand() / RAND_MAX) > p[0])

{

Ti.push_back(-log(tmp) / lambda[1]);

}

else

{

Ti.push_back(-log(tmp) / lambda[0]);

}

}

write("m1", Ti, 1);

}
void model2()

{

vector Ti;

for (int i = 0; i < N; ++i)

{

double first = -log((double)rand() / RAND_MAX) / lambda[0];

double second = -log((double)rand() / RAND_MAX) / lambda[1];

Ti.push_back(min(first, second));

}

write("m2", Ti, 2);

}
void model3()

{

vector Ti;

double first = 0, second = 0;

for (int i = 0; i < N; ++i)

{

double tmp = ((double)rand() + 1) / RAND_MAX;

first = -log(tmp) / lambda[0];

tmp = ((double)rand() + 1) / RAND_MAX;

second = -log(tmp) / lambda[1];

Ti.push_back(max(first, second));

}

write("m3", Ti, 3);

}
int main()

{

model1();

model2();

model3();

}

---

Смотрите также файлы

• Тема Знакомство с базой практики Задание Собрать сведения со страниц сайта учреждения об одном учителе начальных классов Ф. И. О.docx

• Исследование влияния показателя пол сотрудника.docx

• Биография Мэрилин Монро без семьи.docx

• Теплолечение.pptx

• Пояснительная записка к курсовой работе по дисциплине Оптимальное управление системами производственной и технической эксплуатации ттм и нефтегазового оборудования .docx