Файл: Закон больших чисел.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 17.01.2024

Просмотров: 34

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

  1. Вероятностная мера

  2. Классическое вероятностное пространство

  3. Условная вероятность, формула умножения вероятностей

  4. Формулы полной вероятности и Байеса

  5. Независимость событий

  6. Биноминальная случайная величина – число успехов в схеме Бернулли

  7. Гипергеометрическая модель

  8. Равномерное распределение в отрезке

  9. Нормальная вероятностная модель

  10. Показательное распределение

  11. Функция распределения случайной величины

  12. Функция распределения случайного вектора

  13. Дискретный тип распределения, функция вероятностей

  14. Абсолютно непрерывный тип распределения, функция плотности

  15. Маргинальная функция распределения

  16. Медиана и квартили распределения

  17. Математическое ожидание дискретной случайной величины

  18. Математическое ожидание абсолютно непрерывной случайной величины

  19. Свойства дисперсии

  20. Правило 3-х сигм

  21. Независимость случайных величин

  22. Критерий независимости случайных величин через функцию плотности

  23. Критерий независимости случайных величин через функцию распределения

  24. Линейная среднеквадратическая регрессия

  25. Коэффициент корреляции

  26. Сходимости по вероятности

  27. Сходимость по распределению (слабая)

  28. Центральная предельная теорема

  29. Закон больших чисел

  30. Дискретная цепь Маркова



  1. Вероятностная мера

Пусть дано ???? – пространство элементарных исходов, ???? – сигма-алгебра измеримых подмножеств ????. Функция P : ???? ↦ [0, 1], приписывающая каждому измеримому подмножеству неотрицательное значение называется вероятностной мерой, если:

  1. Оно принимает значения от нуля до единицы

  2. Вероятность достоверного события омега (подкова) равна единице. Вероятность невозможного события равна нулю.

  3. Свойство сигма-аддитивности (т. е. вероятность объединения пересекающихся событий равна сумме вероятностей) для любого набора непересекающихся подмножеств.

Доп.

«Измеримых» означает что для них мы можем вычислить вероятность

В пункте три при эквивалентном распределении вместо сигма-аддитивности требуется условие конечной аддитивности и условие непрерывности.

Условие непрерывности это значит вероятность возрастающей последовательности или убывающей, вероятность этих событий равна предельному значению.

  1. Классическое вероятностное пространство

Задается для конечного множества. Пусть ???? (омега) – конечное множество. Классический способ задания вероятностной меры:



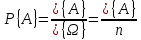
#{A} – количество элементов множества А, #{ ????} – количество всех событий.

Решетка означает количество элементов.

Вероятность каждого элемента равна , n – общее число элементов.

  1. Условная вероятность, формула умножения вероятностей

Условная вероятность определяется для событий, которые имеют положительную вероятность (потому что они в знаменателе будут).

Тогда условная вероятность события А относительно события В (т. е. вероятность А при условии, что произошло В):



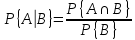
Вероятность пересечения этих событий деленное на вероятность условия.

Если перейти к общему знаменателю, то получим формулу умножения вероятностей:



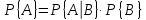
  1. Формулы полной вероятности и Байеса

Формула определяется для полной группы событий (т. е. события, которые не пересекаются, имеют положительную вероятность и в сумме дают единицу). Тогда полная вероятность равна:



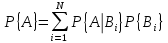
Т. е. условная вероятность, умноженная на вероятность условия.

Формула Байеса:



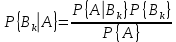
В знаменателе P{A} - формула полной вероятности, не расписываю, просто стрелочку от предыдущей формулы проведи вниз.

  1. Независимость событий

Пара событий называется несовместной если для них вероятность пересечения равна произведению вероятностей:



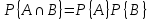
Независимость в совокупности определяется для некой совокупности различных событий, например . Вероятность любых сочетаний подмножеств равна произведению вероятностей.



Доп.

Если попарно выполняется то не обязательно будет независимость. Существуют примеры, для которых попарная независимость не влечет независимость совокупности.

  1. Биноминальная случайная величина – число успехов в схеме Бернулли

Биноминальная случайная величина используется для описания ситуаций, когда подсчитывается количество «успехов» в n независимых испытаниях.

Вероятность того, что в n испытаниях с постоянной вероятностью успеха p, произойдет ровно k «успехов» равна:



  1. Гипергеометрическая модель

Используется для описания ситуаций, когда у нас имеется урна N элементов, в которых всего два типа этих элементов. Например M – белые шары, К – красные шары. Из урны без возвращения отбираются ровно n шаров. Мы хотим узнать, что в этой выборке будет ровно m белых шаров.



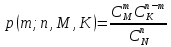
Доп.

Эти значки С – биномиальный коэффициент, он означает число всех возможных вариантов выборки k элементов из множества n.





  1. Равномерное распределение в отрезке

Равномерное распределение характеризуется тем, что вероятность любого интервала [c, x] из подмножества [a, b] пропорциональна длине этого интервала и не зависит от его расположения.



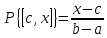
Равномерное распределение — это абсолютно непрерывное распределение с постоянной плотностью

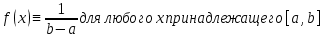
  1. Нормальная вероятностная модель

Нормальная вероятностная модель – абсолютно непрерывная модель с функцией плотности:



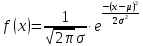
(Последняя дробь — это все степень, экспонента в степени)

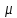– это математическое ожидание, 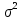- дисперсия

  1. Показательное распределение

Показательное распределение – это показательная модель срока службы объектов с постоянной интенсивностью отказов. Для нее вероятность «прожития» больше t времени («дожить до t») равна 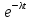. Коэффициент лямбда – это интенсивность отказов.



, где i – количество объектов

  1. Функция распределения случайной величины

Пусть дана случайная величина i. Тогда функция распределения случайной величины равна:



Доп.

Свойства:

  1. Функция распределения случайной величины на минус бесконечности равна нулю.

  2. На плюс бесконечности равна единице.

  3. Вероятность попадания случайной величины в интервал: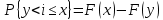



  1. Функция распределения случайного вектора



Доп.

В формуле запятая интерпретируется как «и», т. е. мы можем поставить вместо запятой знак пересечения.

Свойства:



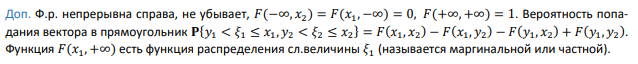
  1. Дискретный тип распределения, функция вероятностей



  1. Абсолютно непрерывный тип распределения, функция плотности

Принадлежит абсолютно непрерывному типу если вероятность любого события вычисляется как интеграл по этому событию относительно функции плотности f(x) по dx, где функция плотности положительная функция, интеграл от которой равен единице.


Эта же запись в математическом виде:



Доп.

Если в первой функции B заменить на интервал от минус бесконечности до x, то станет функция распределения:



И в этом случае, для функции распределения, функция плотности это производная функции распределения.

  1. Маргинальная функция распределения

Маргинальные функции распределения – это функции распределения компонента случайного вектора.

Пусть дана совместная 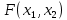- функция распределения случайного вектора Она вычисляется по формуле:





  1. Медиана и квартили распределения

Квантиль порядка альфа распределения случайной величины определяется как . Квантиль — это решение уравнения 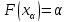. Этого решения может не быть, т. е. функция может иметь скачок в этом месте, поэтому надо как-то по-другому определить.

Медиана – это квантиль порядка .

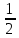Первый квартиль — это квантиль порядка 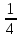, третий квартиль – это квантиль порядка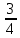



  1. Математическое ожидание дискретной случайной величины



Смотрите также файлы