Файл: Закон больших чисел.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 17.01.2024

Просмотров: 35

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


  1. Математическое ожидание абсолютно непрерывной случайной величины

Абсолютно непрерывная величина должна задаваться функцией плотности.



  1. Свойства дисперсии



А – способ вычисления (мат. ожидание квадрата минус квадрат мат. ожидания)

B – от сдвига (просто плюс b) дисперсия не меняется. От масштабирования (константа а) – масштаб выносится с квадратом

С –

D – дисперсия суммы независимых случайных величин равна сумме дисперсий

  1. Правило 3-х сигм

Вероятность попасть в интервал средний плюс-минус 3 сигмы – это не меньше, чем 8/9 всегда.



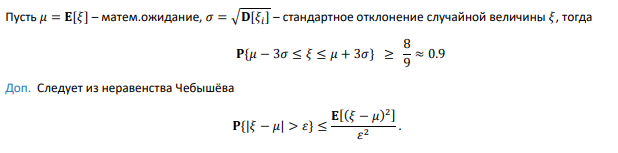
  1. Независимость случайных величин

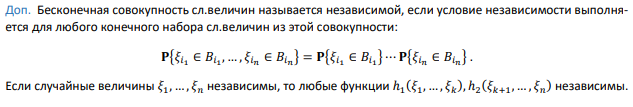
Даны случайные величины и они независимы если у них выполняется соотношение:





  1. Критерий независимости случайных величин через функцию плотности



  1. Критерий независимости случайных величин через функцию распределения



  1. Линейная среднеквадратическая регрессия

Линейная среднеквадратическая регрессия – это минимум среднеквадратической ошибки прогноза одной случайной величины посредством линейной функции другой случайной величины.



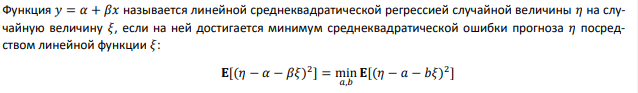
Если минимум брать по всем функциям, а не только по линейным. Это будет называться уже не линейной, а просто среднеквадратическая регрессия:



  1. Коэффициент корреляции



Если попадется – пояснение свойств в консультации, время 40:20.

  1. Сходимости по вероятности



  1. Сходимость по распределению (слабая)



  1. Центральная предельная теорема



  1. Закон больших чисел



  1. Дискретная цепь Маркова

Смотрите также файлы