ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 17.01.2024
Просмотров: 63
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Объемы шарового сегмента, шарового слоя и шарового сектора
Определение:
Итак, шар – это совокупность всех точек пространства, находящихся от данной точки на расстоянии, не больше данного. Причём, данная точка называется центром шара, а данное расстояние – радиусом шара.
Определение:
Шаровым сегментом называется часть шара, отсекаемая от него какой-нибудь плоскостью.
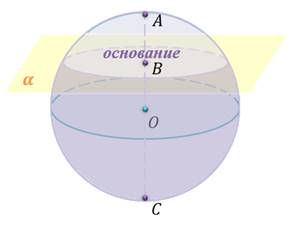
Утверждение: если радиус шара равен
, а высота сегмента равна 
, то объем 
шарового сегмента можно вычислить по формуле:
Определение:
Шаровым слоем называется часть шара, заключённая между двумя параллельными секущими плоскостями.
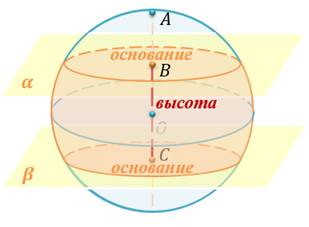
Круги, получившиеся в сечении шара плоскостями, называются основаниями шарового слоя, а расстояние между плоскостями – высотой шарового слоя.
Нетрудно заметить, что объём шарового слоя можно вычислить, как разность объёмов двух шаровых сегментов.
Если высота шарового слоя равна
, а радиусы 
и 
– радиусы оснований шарового слоя соответственно, то объем шарового слоя можно вычислить по формуле:
Определение:
Шаровым сектором называется тело, которое получается при вращении кругового сектора с углом, меньшим 90о, вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов.
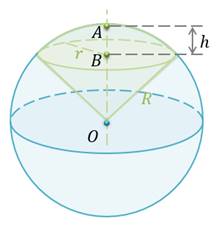
Если радиус шара равен
, а высота шарового сегмента равна 
, то объем 
шарового сектора можно найти по формуле:
Задача: радиус шара равен
см. Вычислите объем шарового сегмента, если его высота равна 
см.
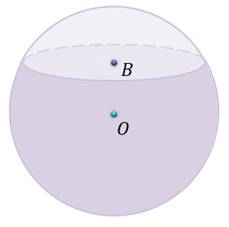
Решение: запишем формулу для вычисления объёма шарового сегмента.
И подставим в неё радиус шара и высоту шарового сегмента.
Задача: по разные стороны от центра шара проведены два параллельных сечения с площадью
и 
см2. Расстояние между сечениями равно 
см. Определите объём получившегося шарового слоя.
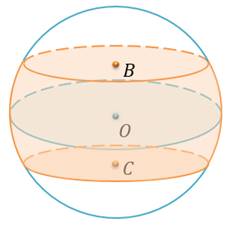
Решение: запишем формулу для вычисления объема шарового слоя.
Чтобы найти объём шарового слоя нам необходимо знать его высоту и радиусы двух его оснований.
По условию задачи нам дано расстояние между сечениями, как раз-таки это расстояние и есть высота данного шарового слоя, и она равна
. Теперь найдём чему равны радиусы оснований шарового слоя. Напомню, что сечением шара плоскостью является круг. Площадь круга вычисляется по формуле
. Отсюда найдём радиусы оснований шарового слоя. Тогда имеем, радиус одного основания равен 
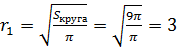(см), радиус второго основания равен 
(см).Подставим радиусы оснований и высоту шарового слоя в формулу его объёма. Посчитаем. Получаем, что объём данного шарового слоя равен
.Задача: радиус шара равен
см. Найдите объем шарового сектора, если высота шарового сегмента равна 
см.
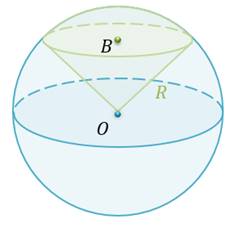
Решение: запишем формулу для вычисления объёма шарового сектора.
Подставим в неё радиус шара и высоту шарового сегмента. Посчитаем. Получим, что объём данного шарового сектора равен
.