Файл: Практическая работа Тема. Вычисление вероятностей событий по классической формуле определения вероятностей с использованием элементов комбинаторики.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 18.01.2024
Просмотров: 176
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ПРАКТИЧЕСКАЯ РАБОТА № 1.
Тема. Вычисление вероятностей событий по классической формуле определения вероятностей с использованием элементов комбинаторики.
Цель: вычисление вероятностей событий по классической формуле определения вероятности, развитие самостоятельной мыслительной деятельности, вычислительных навыков, творческого мышления студентов.
Порядок выполнения работы:
1. Ознакомиться с основными формулами комбинаторики (размещения, сочетания, перестановки).
2. Рассмотреть примеры решения комбинаторных задач.
3. Ознакомиться с формулой классического определения вероятности.
4. Рассмотреть примеры решения задач на применение формулы классического определения вероятности и с использованием элементов комбинаторики.
5. Ответить на контрольные вопросы.
6. Получить и выполнить индивидуальные задания.
Теоретическая часть.
Комбинаторика.
Перестановками из n элементов называют такие соединения, которые отличаются друг от друга порядком расположения элементов.
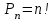
Размещениями из n элементов по m в каждом называют такие соединения, которые отличаются друг от друга либо самими элементами, либо порядком их расположения.
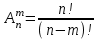 .
.Сочетаниями из n элементов по m в каждом называют такие соединения, которые отличаются друг от друга хотя бы одним элементом.
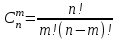 .
.Пример 1.
Вычислите:
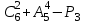
Решение:
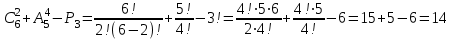 .
.Пример 2.
Сколько можно записать двузначных чисел, используя без повторения
все 10 цифр?
Решение:
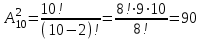 .
.Классическое определение вероятности.
События, явления могут быть достоверными
, невозможными и случайными. Те события, которые обязательно произойдут при осуществлении определённой совокупности условий (которую будем называть опытом или испытанием), называют достоверными и обозначают U. Событие, которое заведомо не произойдет, если будет осуществлена определенная совокупность условий, называют невозможным и обозначают V. События, которые при испытании могут произойти, а могут и не произойти, называют случайными и обозначают - А, В, С.
Случайные события называются несовместными, если каждый раз возможно появление только одного из них. События называются совместными, если в данных условиях появление одного из них не исключает появление другого при том же испытании. События называются противоположными, если в условиях испытания они, являясь единственными его исходами, несовместны. Случайные события бывают элементарные и составные. Множество всех элементарных событий, связанных с некоторым опытом, называется пространством элементарных событий (U). Каждое событие определяется как подмножество во множестве элементарных событий A. При этом те элементарные события из U, при которых событие А наступает (т.е. принадлежит подмножеству А), называются благоприятствующими событию А.
Пусть
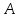 - случайное событие, связанное с некоторым опытом. Повторим опыт
- случайное событие, связанное с некоторым опытом. Повторим опыт 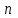 раз в одних и тех же условиях и пусть при этом событие
раз в одних и тех же условиях и пусть при этом событие 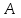 появилось
появилось 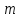 раз.Отношение
раз.Отношение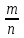 числа
числа 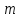 опытов, в которых событие
опытов, в которых событие 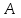 появилось, к общему числу
появилось, к общему числу 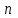 проведённых опытов называется частотой события
проведённых опытов называется частотой события 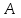 .
.Постоянная величина р, к которой все более приближается частота событий А при достаточно большом повторении опыта
, называется вероятностью события А и обозначается
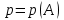 .
.Рассмотрим конечное пространство элементарных событий
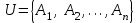 , где
, где 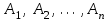 - попарно несовместные и равновозможные элементарные события. Пусть некоторому событию А благоприятствуют т из п элементарных событий пространства U.
- попарно несовместные и равновозможные элементарные события. Пусть некоторому событию А благоприятствуют т из п элементарных событий пространства U. Вероятностью события р(А) называется отношение числа т элементарных событий, благоприятствующих событию А, к общему числу п равновозможных элементарных событий:
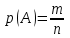 (1)
(1)Из определения вероятности вытекают следующие её свойства:
1. Вероятность любого события
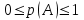 ;
; 2. Вероятность достоверного события
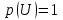 , так как
, так как 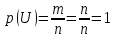 ;
; 3. Вероятность невозможного события
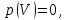 так как
так как 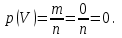
Примеры по выполнению практической работы
Пример 1.В урне 3 белых и 9 черных шаров. Из урны наугад вынимают один шар. Какова вероятность того, что вынутый шар окажется черным (событие А)?
Решение: Имеем п = 12, т = 9, и поэтому
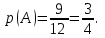
Пример 2. Подбрасывают две игральные кости. Найти вероятность того, что на них в сумме выпадает 6 очков (событие А).
Решение:При подбрасывании двух игральных костей общее число равновозможных элементарных исходов
равно числу пар
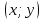 где х и у принимают значения 1, 2, 3, 4, 5, 6:
где х и у принимают значения 1, 2, 3, 4, 5, 6: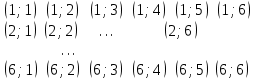
т.е.
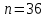 . Событию А благоприятствуют пять пар:
. Событию А благоприятствуют пять пар: 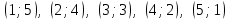 , т.е.
, т.е. 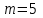 . Следовательно, искомая вероятность
. Следовательно, искомая вероятность 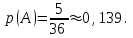
Пример 3. В урне
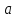 белых и
белых и 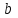 чёрных шаров. Из урны наугад вынимают
чёрных шаров. Из урны наугад вынимают 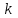 шаров. Найти вероятность того, что среди них будет
шаров. Найти вероятность того, что среди них будет 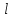 белых, а следовательно,
белых, а следовательно, 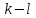 чёрных
чёрных 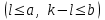 .
.Решение: Число элементарных событий
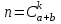 . Подсчитаем число элементарных событий, благоприятствующих интересующему нас событию
. Подсчитаем число элементарных событий, благоприятствующих интересующему нас событию 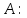 среди
среди 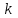 взятых шаров будет
взятых шаров будет 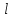 белых и
белых и 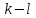 чёрных. Очевидно, что число способов, которыми можно выбрать
чёрных. Очевидно, что число способов, которыми можно выбрать 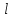 белых шаров из
белых шаров из 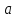 , равно
, равно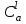 , а число способов, которыми можно к ним «довыбрать»
, а число способов, которыми можно к ним «довыбрать» 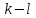 чёрных шаров, равно
чёрных шаров, равно 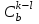 . Каждая комбинация белых шаров может сочетаться с каждой комбинацией чёрных, поэтому
. Каждая комбинация белых шаров может сочетаться с каждой комбинацией чёрных, поэтому 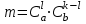 . Следовательно,
. Следовательно, 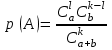 .
.Контрольные вопросы.
-
Сформулируйте определение сочетания, размещения, перестановки. -
Запишите формулу для нахождения сочетания, размещения, перестановки -
Какое событие называют достоверным? -
Какое событие называют невозможным? -
Дайте определение противоположных событий. -
Сформулируйте классическое определение вероятности. -
Чему равна вероятность достоверного события? -
Чему равна вероятность невозможного события? -
Что называется частотой события?
Индивидуальные задания к практической работе № 2.
Тема. Вычисление вероятностей событий по классической формуле определения вероятностей с использованием элементов комбинаторики.
1 вариант.
1. Вычислить: 1)
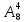 ; 2)
; 2) 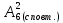 ; 3)
; 3) 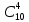 ; 4)
; 4) 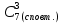 ;
;5)
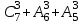 ; 6)
; 6) 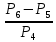 .
. 2. Сколькими способами могут разместиться пять человек вокруг круглого стола?
3. Сколько двузначных чисел можно составить из цифр 1;2;5;8;9 так чтобы в каждом числе не было одинаковых цифр?
4. В бригаде из двадцати пяти человек нужно выделить четырех для работы на определенном участке. Сколькими способами это можно сделать?
5. Каждая буква слова СТАТИСТИКА написана на разных карточках. Сколькими различными способами можно переставить эти буквы?
6. В ящике имеется 15 деталей, среди которых 10 окрашенных. Сборщик наудачу извлекает 3 детали. Найти вероятность того, что извлеченные детали окажутся окрашенными.
7. В цехе работают 10 мужчин и 5 женщин. По табельным номерам наудачу отобраны 7 человек. Найти вероятность того, что среди отобранных лиц окажутся 3 женщины.
8. В урне 10 белых и 5 черных шаров. Сколькими способами можно наугад вынуть 3 шара, чтобы 2 шара оказались белыми, а один черным?
2 вариант.
1. Вычислить: 1)
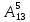 ; 2)
; 2) 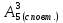 ; 3)
; 3) 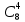 ; 4)
; 4) 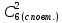 ;
;