Файл: Решение с помощью метода сечений, определим крутящие моменты на участках вала, начиная расчет со свободного конца.doc

Скачать файл (0,47Мб)

Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 18.01.2024

Просмотров: 9

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

Контрольная работа №2
Задача №8
Для заданного бруса построить эпюры продольных сил и нормальных напряжений в поперечных сечениях бруса, проверить прочность бруса на каждом участке, приняв значение допускаемого напряжения для стали

_р =160 МПа, на сжатии

_р =120 МПа, а также определить перемещение свободного конца бруса. Модуль продольной упругости Е=2·10⁵ МПа. Вес бруса не учитывать.
Дано: F₁=15 кН; F₂=2 кН; А₁=1,2 см²; А₂=1,4 см²;
Р

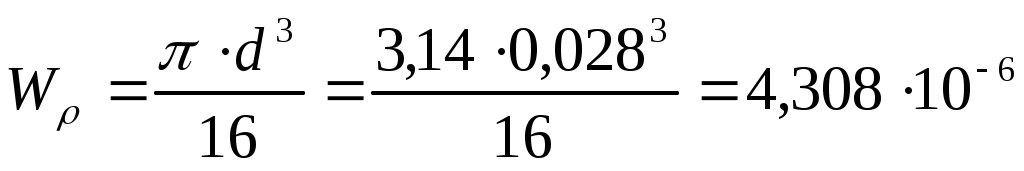ешение:
1. Разделим брус на участки, начиная от свободного конца. Границами участков являются сечения, в которых приложены внешние силы, и место изменения размеров поперечных сечений.

2.Используя метод сечений, определяем значения продольной силы на каждом участке:
N₁=-F₁=-15 кН;

N₂= -F₁=-15 кН;

N₃=-F₁-F₂=-15-2=-17 кН
На всех участках бруса действует деформация сжатия
3.По полученным значениям строим эпюру продольных сил.

4.Вычисляем значения нормальных напряжений на каждом участке.

5.Строим эпюру нормальных напряжений.

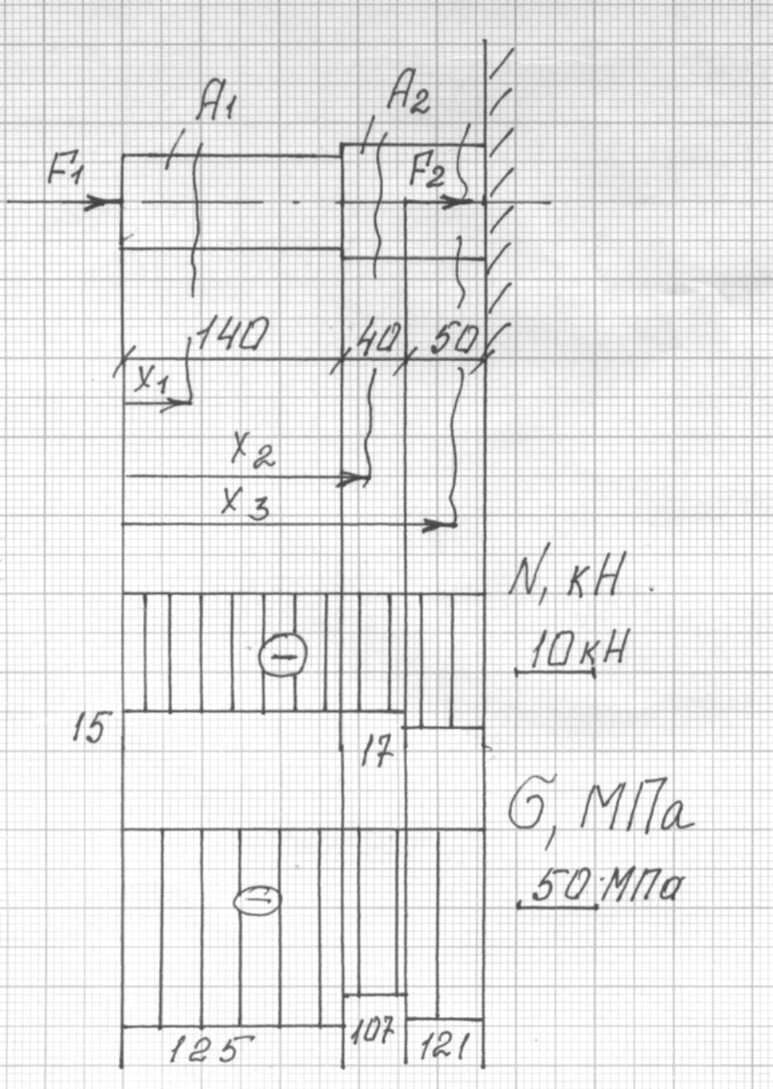
6.Проверяем брус на прочность. На первом и третьем участках условие прочности не выполняется

6. Определяем перемещение свободного конца бруса используя формулу Гука:

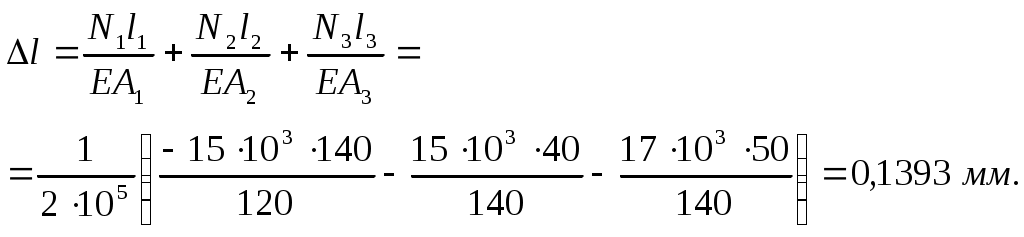
Ответ: брус станет короче на

Задача №15

Для заданного вала круглого поперечного сечения построить эпюру крутящих моментов и определить диаметр, обеспечив его прочность и жесткость, если

МПа;

рад/м; G=810⁴ МПа; М₁=4,2 кНм М₂=2 кНм М₃=1,2 кНм
Дано:

МПа;

рад/м; G=810⁴ МПа; М₁=4,2 кНм М₂=2 кНм М₃=1,2 кНм

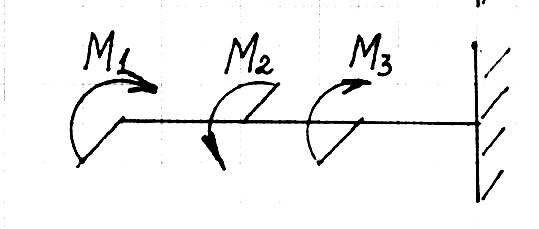
Решение:
С помощью метода сечений, определим крутящие моменты на участках вала, начиная расчет со свободного конца
1-1 М_Z₁=-М₁=-4,2 кНм
2-2 М_Z₂=-М₁+М₂=-4,2+2,0=-2,2 кНм
3-3 М_Z₃=-М₁+М₂-М₃=-4,2+2,0-1,2=-3,4 кНм

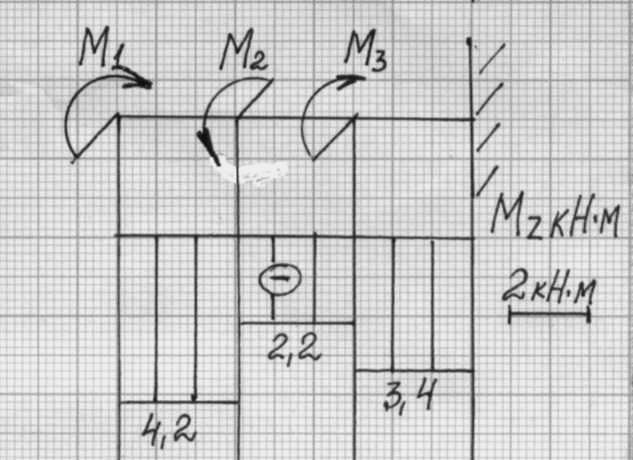
Из эпюры крутящих моментов видно, что максимальный крутящий момент на первом участке
M_Zmax=4,2 кНм
Из условия прочности вала на кручение

определяем необходимый полярный момент сопротивления поперечного сечения вала:

мм³=60 см³
Определяем необходимый диаметр вала.

то

см
Полученный диаметр округляем до ближайшего большего стандартного значения d=68 мм
Из условия прочности вала на жесткость

определяем необходимый полярный момент инерции поперечного сечения вала:

м⁴=262,5 см⁴
Определяем необходимый диаметр вала.

то

см
Полученный диаметр округляем до ближайшего большего стандартного значения d=72 мм

Требуемый размер сечения получился больше из расчета на жесткость, поэтому его принимаем как окончательный

Ответ: d=72 мм
Задача №39
Для двухопорной балки построить эпюры поперечных сил и изгибающих моментов. Подобрать сечение балки, составленное из двух швеллеров, если

=160 МПа
Дано:
F

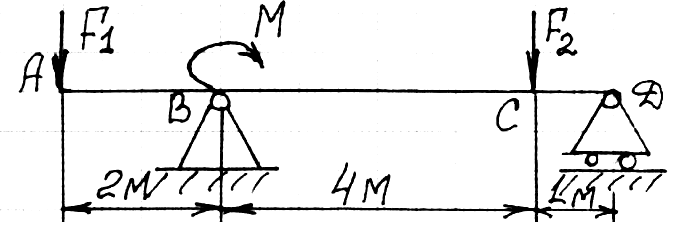₁=14 кН; F₂=8 кН; M=8 кНм

Решение;
Определим опорные реакции балки, для чего предварительно составим уравнения равновесия:

Решаем систему уравнений:

кН

кН
Делаем проверку :

Опорные реакции определены верно.
Делим балку на участки по характерным точкам.

Определяем поперечные силы в характерных точках.
Q_А=-F₁=-14 кН

кН

кН
Определяем изгибающие моменты в характерных точках

кНм

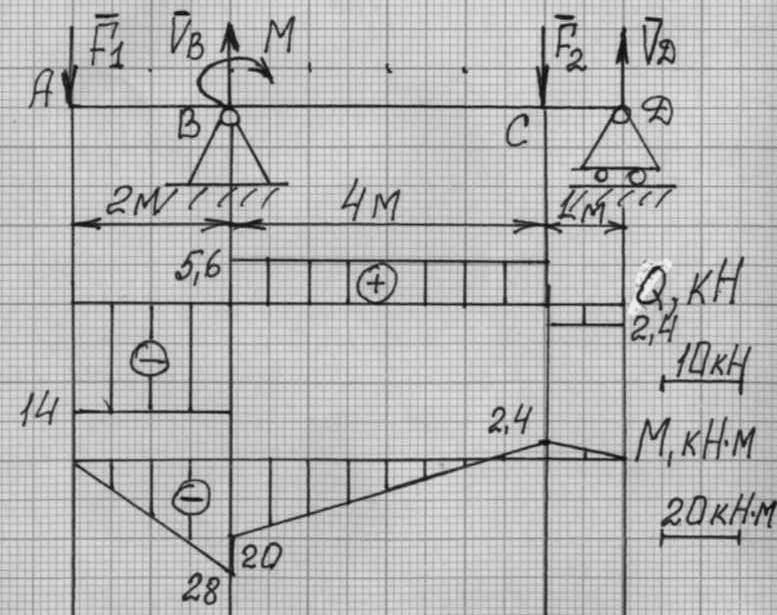
Из эпюры изгибающих моментов определим максимальный изгибающий момент:

M_Xmax=28 кНм

Из условия прочности балки на изгиб

определим необходимый осевой момент сопротивления поперечного сечения балки:

мм³=175 см³
Для одного швеллера расчетный момент сопротивления:

см³
Принято швеллер №16 у которого W_x=93,4 см³

Задача 25
Торсионная рессора представляет собой прямой стержень 2, один конец которого укреплен во втулке 1, установленной, например на раме тележки, а другой жестко связан с рычагом 4, который соединяется с обрессорной частью, например надрессорной балкой. Второй опорой стержня 2 служит подшипник 3, также укрепленный на раме тележки. Определить длину а рычага, угол закручивания , вертикальное перемещение точек приложения сил (прогиб) f жесткости торсиона, если G =810⁴ МПа;

=80 МПа; F=800 Н; d=28 мм; L=700 мм

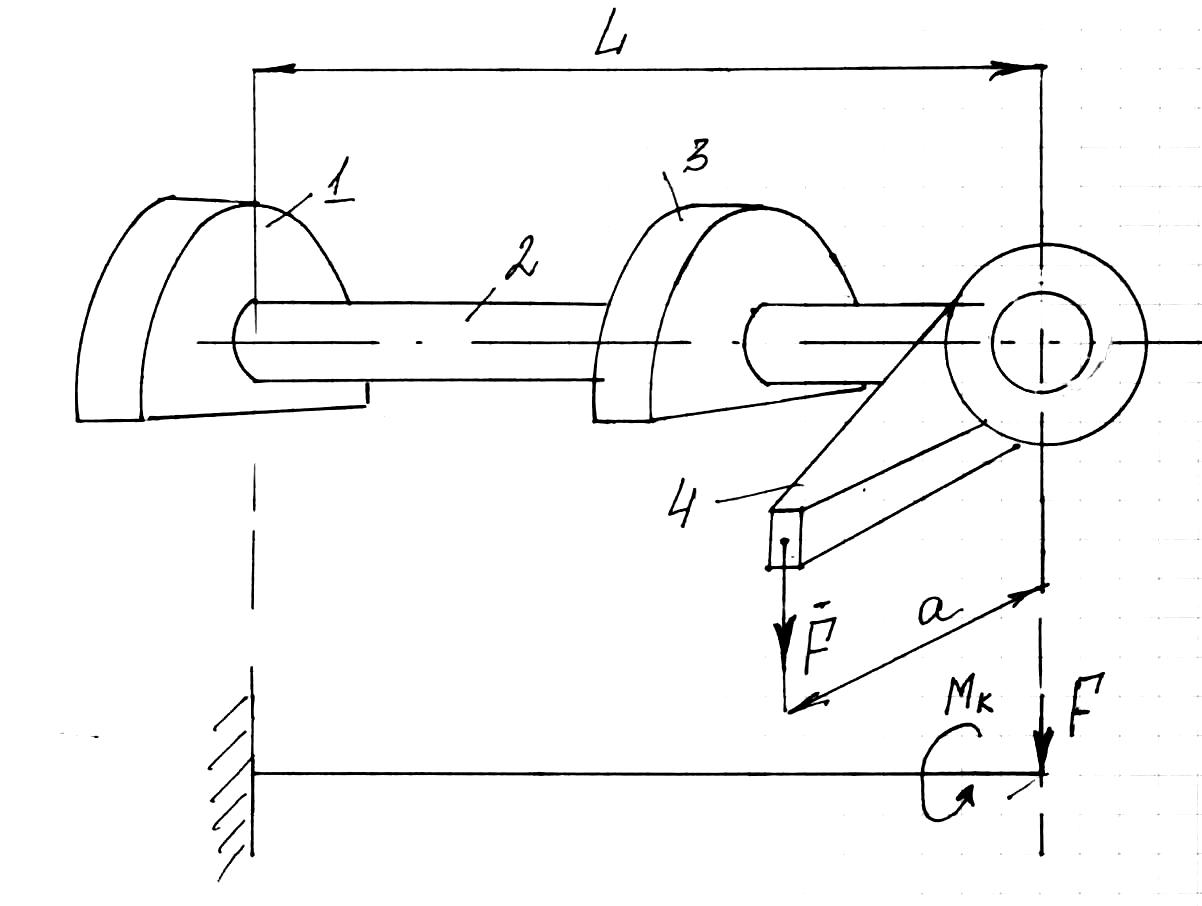
Решение
Торсион работает на скручивание, поэтому максимально допустимый крутящий момент в его сечении можно определить исходя из условия прочности на кручение