Файл: Синтез комбинационных устройств канонические формы представления логических функций.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 69
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СИНТЕЗ КОМБИНАЦИОННЫХ УСТРОЙСТВ
Канонические формы представления логических функций.
Синтез логического устройства распадается на несколько этапов. На первом этапе требуется функцию, заданную в словесной, табличной или другой формах, представить в виде логического выражения с использованием некоторого базиса. Следующие этапы сводятся к получению минимальных форм функций, обеспечивающих при синтезе наименьшее количество электронного оборудования и рациональное построение функциональной схемы устройства. Для начального представления функции обычно используется базис И, ИЛИ, НЕ независимо от того, какой базис будет использоваться для построения логического устройства.
Исходными, из соображений удобства последующих преобразований, приняты следующие две канонические формы представления функций: совершенная дизъюнктивная нормальная форма (СДНФ) и совершенная конъюнктивная нормальная форма (СКНФ).
Совершенная дизъюнктивная нормальная форма (СДНФ).
Дизъюнктивной нормальной формой (ДНФ) называется такая форма представления функции, при которой логическое выражение функции строится в виде дизъюнкции ряда членов, каждый из которых является простой конъюнкцией аргументов или их инверсий.
Примером ДНФ может служить выражение
 | (3.9) |
Приведем форму представления функций, не являющейся ДНФ. Например, функция
представлена не в ДНФ, так как последний член не является простой конъюнкцией аргументов.
Также не является ДНФ следующая форма представления функции:
Если в каждом члене ДНФ представлены все аргументы (или их инверсии) функции, то такая форма носит название совершенной дизъюнктивной нормальной формы (СДНФ). Выражение (3.9) не является СДНФ, так как в нем лишь третий член содержит все аргументы функции.
Для перехода от ДНФ к СДНФ необходимо в каждый из членов, в которых представлены не все аргументы, ввести выражение вида , где xi — отсутствующий в члене аргумент. Так как , такая операция не может изменить значений функции. Покажем переход от ДНФ к СДНФ на примере следующего выражения:
Добавление в члены выражений вида приведет функцию к виду
На основании (3.1)
Отсюда после приведения подобных членов:
Полученная форма является СДНФ. Если исходная функция дана в табличной форме, то СДНФ может быть получена непосредственно.
Пусть дана функция в форме табл. 3.4. Для этой функции СДНФ имеет вид
 | (3.10) |
| Таблица 3.4 | ||||||||
| x1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| x2 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| x3 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| f(x1,x2,x3) | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 |
Как видно из выражения (3.10), в нем каждый член соответствует определенному набору значений аргументов, при котором функция равна 1. Каждый из наборов аргументов, при которых равна 1 (3, 4, 6, 8-й столбцы наборов), обращает в единицу соответствующий член выражения (3.10), вследствие чего и вся функция оказывается раиной единице.Можно сформулировать следующее правило записи СДНФ функции, заданной таблицей истинности.
Необходимо записать столько членов в виде конъюнкций всех аргументов, сколько единиц содержит функция в таблице. Каждая конъюнкция должна соответствовать определенному набору значений аргументов, обращающему функцию в единицу, и если в этом наборе значение аргумента равно нулю, то в конъюнкцию входит .инверсия данного аргумента.
Следует отметить, что любая функция имеет единственную СДНФ.
Совершенная конъюнктивная нормальная форма (СКНФ).
Конъюнктивной нормальной формой (КНФ) называется форма представления функции в виде конъюнкции ряда членов, каждый из которых является простой дизъюнкцией аргументов (или их инверсий).
Примером КНФ может служить следующая форма представления функции:
Приведем формы представления функций, не являющиеся КНФ:
(здесь третий член не является простой дизъюнкцией аргументов или их инверсий);
(эта форма также не является КНФ, так как в ней первый член не связан с остальными операцией конъюнкции).
В совершенной конъюнктивной нормальной форме (СКНФ) в каждом члене КНФ должны быть представлены все аргументы.
Для перехода от КНФ к СКНФ необходимо добавить к каждому члену, не содержащему всех аргументов, члены вида , где хi — аргумент, не представленный в члене. Так как
, то такая операция не может повлиять на значение функции.Добавление к некоторому члену образует выражение вида , которое можно привести к виду
Справедливость данного равенства вытекает из распределительного закона;
она может быть показана также путем раскрытия скобок в правой части выражения:
так как Рассмотрим переход от КНФ к СКИФ на примере функции
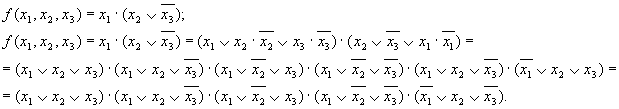
Покажем применение распределительного закона прн проведении использованных здесь преобразований над одним из членов выражения
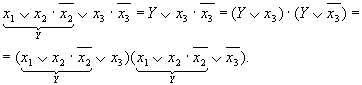
Обозначим Тогда на основании распределительного закона
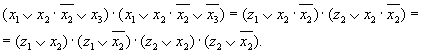
Далее обозначим и вновь применим распределительный закон
Подставив сюда значения z1 и z2 получим соответствующие члены приведенного выше выражения при переходе от КНФ к СКНФ.
Совершенная КНФ функции легко строится по таблице истинности.
Рассмотрим в качестве примера функцию, приведенную в табл. 3.4; СКНФ этой функции имеет вид
 | (3.11) |
Выражение содержит столько членов, связанных операцией конъюнкции, сколько нулей имеется среди значений функции f(x1, x2, x3) в таблице истинности. Таким образом, каждому набору значений аргументов, на котором функция равна нулю, соответствует определенный член СКНФ, принимающий на этом наборе значение нуль. Так как члены СКНФ связаны операцией конъюнкции, при обращении в нуль одного из членов и вся функция оказывается равной нулю.
Таким образом, можно сформулировать следующее правило записи СКНФ функции, заданной таблицей истинности.
Следует записать столько конъюнктивных членов, представляющих собой дизъюнкции всех аргументов, при скольких наборах значений аргументов функция равна нулю, и если в наборе значение аргумента равно единице, то в дизъюнкцию входит инверсия этого аргумента. Любая функция имеет единственную СКНФ.
Структурная схема логического устройства может быть построена непосредственно по канонической форме (СДНФ или СКНФ) реализуемой функции. Получающиеся при этом схемы для функций (3.10) и (3.11) показаны на рис. 3.26, а и б. Недостаток такого метода построения структурных схем, обеспечивающего, в общем, правильное функционирование устройства, состоит в том, что получающиеся схемы, как правило, оказываются неоправданно сложными, требуют использования большого числа логических элементов и, следовательно, имеют низкие экономичность и надежность.
Во многих случаях удается так упростить логическое выражение, не нарушая функции, что соответствующая структурная схема оказывается существенно более простой.
Методы такого упрощения функции, называемые методами минимизации функций, рассматриваются ниже.
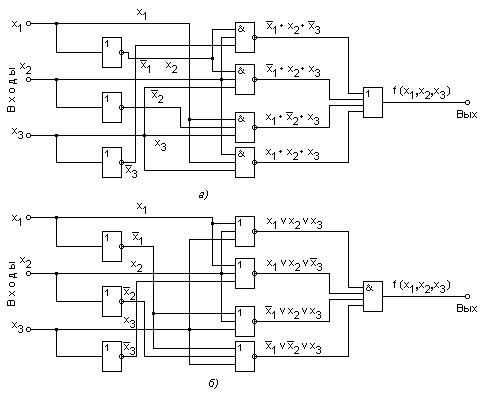
рис 3.26