Рассмотрим минимизацию с помощью карты Вейча функции трех аргументов, представленной табл. 3.13.

Все клетки, содержащие 1, охватываются двумя областями. В каждой из областей 2¹ клеток. Таким образом, для них n – k = 3 – 1 = 2 и эти области в МДНФ будут представлены членами, содержащими по две буквы. Первой обласги соответствует член x_1? x₂ (аргумент x₃ здесь не присутствует, так как для одной клетки этой области он имеет значение без инверсии, для другой — с инверсией); второй области соответствует член . Следовательно, МДНФ функции



Рассмотрим пример минимизации функции четырех аргумен. тов. заданной табл. 3.14.

Первая и четвертая области имеют по две клетки, для них n – k = 4 – 1 = 3. Эти области будут в МДНФ представлены членами, содержащими по три буквы.

Вторая и третья области содержат по четыре клетки и в МДНФ выражаются членами, содержащими по две буквы (n – k = 4 – 2 = 2).

Минимальная ДНФ функции имеет вид



При построении замкнутых областей допускается сворачивание карты в цилиндр с объединением се противоположных граней. В силу этого крайние клетки строки или столбца таблицы рассматриваются как соседние и могут быть объединены в общую область, Иллюстрацию этого приема проведем на примере функции, представленной табл. 3.15, Минимальная ДНФ функции



В силу допустимости такого сворачиванья карты вдоль горизонтальной и вертикальной осей, например, клетки, расположенные н четырех углах карты функции четырех переменных, оказываются соседними и могут быть объединены в одну область. Покажем это на примере минимизации функции, заданной табл. 3.16. Минимальная ДНФ функции



Для получения МКНФ функции замкнутыми областями охватываются клетки с нулевыми значениями функции, и при записи членов

---

логического выражения берутся инверсии аргументов, на пересечении которых находятся области. Так, для функции, приведенной в табл. 3.17, МКНФ



 

Таблица 3.17

До сих пор здесь рассматривались логические функции с числом аргументов до четырех. Представление функции и минимизация ее с помощью карт Вейча усложняются, если число аргументов больше четырех.

В табл. 3.18 показано представление с помощью карт Вейча функции пяти аргументов.

Таблица истинности здесь состоит из двух карт, каждая из которых представляет собой карту четырех переменных. Одна из них соответствует x₅ = 1, другая – x₅ = 0, Эти карты можно мысленно представить себе расположенными одна над другой (рис. 3.29). При этом области охвата клеток могут быть трехмерными, т. е. одной областью могут охватываться клегки двух карт.

Для приведенной в табл. 3.18 функции МДНФ равна



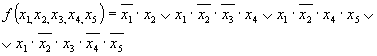
Для минимизации функций с числом аргументов, большим пяти, карты Вейча оказываются неудобными. Минимизация таких функций может быть выполнена методом Квайна.

---

Синтез не полностью заданных логических функций

По условиям работы логического устройства может оказаться, что некоторые наборы значений аргументов являются запрещенными для данного устройства и никогда не могут появляться на его входах. В этом случае функция оказывается заданной не на всех наборах аргументов. Такие функции будем называть не полностью заданными.

При синтезе логического устройства, реализующего не полностью заданную функцию, допустимо произвольно задаваться значениями функции на запрещенных наборах аргументов. При этом в заннсимости от способа задания этих значений функции минимальная фирма может оказаться простой или более сложной. Таким образом, возникает проблема целесообразного доопределения функции на запрещенных наборах аргументов.

Может быть использован следующий способ получения минимальной формы не полностью заданной функции f:

а) записывается СДПФ (СКИФ) функции f₀. полученной из f путем задания значения 0 (значения 1 и случае СНКФ) на всех запрещенных наборах аргументов;

б) записывается СДНФ (СКИФ) функции f₁, полученной из f путем задания значения 1 (значения 0 в случае СКНФ) на всех запрещенных наборах аргументов;

в) функция f₁ приводится к сокращенной форме (к форме, содержащей все простые имплнканты);

г) составляется импликантнзя таблица из всех членов функции f₀ и простых импликант функции f₁;

д) искомая минимальная форма составляется из простых импликант функции f₁, поглощающих все члены СДНФ (СКНФ) функции f₀.

Рассмотрим применение данного метода к минимизации не полностью заданной функции, приведенной в табл. 3.19,

Записываем логическое выражение функции f₀ в СДНФ



Записываем СДНФ функции f₁



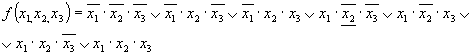
Методом Квайна приводим функцию f₁к сокращенной форме:

Составляем импликантную таблицу (табл. 3.20).

---

Таблица 3.19
x1	0	0	0	0	1	1	1	1
x2	0	0	1	1	0	0	1	1
x3	0	1	0	1	0	1	0	1
f(x1,x2,x3)	*	0	1	*	1	*	*	1

 

Таблица 3.20
Простые импликанты функции f1	Члены СДНФ
	X	X
	X		X
		X	X

 

Минимальная форма логического выражения функции может быть получена исключением любой из трех простых импликант

---

 

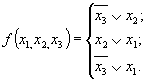
Рассмотрим минимизацию той же функции методом карты Вейча (табл. 3.21).

При минимизации функции данным методом следует на запрещенных наборах аргументов задавать функции такие значения, при которых клетки со значением 1 (либо 0) охватываются минимальным числом областей с максимальным числом клеток в каждой из областей. Применительно к рассматриваемся функции такое доопределение функции может быть осуществлено тремя различными способами, представленными в табл. 3.22. Они приводят к полученным выше выражениям МДНФ функции.

 

---

Смотрите также файлы

• Лекции, напишите эссе Условия профессионального развития личности.docx

• Задача по теме 13 раздела 2 Совершенная конкуренция объем выпуска.docx

• Интерпретация художественного текста. Вопрос 1.doc

• Доклад по дисциплине избранные главы биоорганической химии.docx

• управление персоналом 3.docx