ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.02.2024
Просмотров: 51
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ТЕСТ «ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ»
-
Какая из заданных функций НЕ является функцией двух переменных:
А.
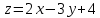 ; Б.
; Б. 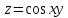 ; В.
; В. 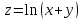 ;
;Г.
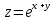 ; Д.
; Д. 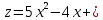 6.
6.2. Выберите НЕправильное утверждение:
А. Функцию двух переменных можно задать в виде таблицы.
Б. Совокупность пар (x,y) значений x и у, при которых определяется функция
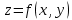 называется областью определения функции.
называется областью определения функции.В. Геометрически уравнение
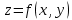 определяет в декартовой системе координат некоторую поверхность.
определяет в декартовой системе координат некоторую поверхность.Г. Область определения функции двух переменных задается в виде множества точек координатной прямой.
Д. Все утверждения правильные.
3. Область определения какой функции задана на рисунке:
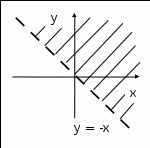
А.
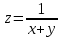 ; Б.
; Б. 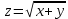 ; В.
; В. 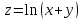 ; Г.
; Г. 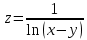 ;
;Д. правильного ответа нет.
4. Значение функции
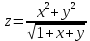 в точке Р(1;2) равняется:
в точке Р(1;2) равняется:А. 1,5; Б. 2,5; В. -1,5; г. -2,5; Д. правильного ответа нет.
5. Найти частные производные первого порядка функции
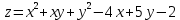 :
:А.
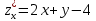 ,
, 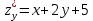 ; Б.
; Б. 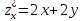 ,
, 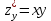 ;
;В.
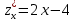 ,
, 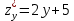 ; Г.
; Г. 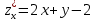 ,
, 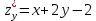
;
Д. правильного ответа нет.
6. Найти частную производную второго порядка по переменной х от функции
 :
:А. 0; Б. 2х+у; В. 2; Г. 2х+у-4; Д. правильного ответа нет
7. Найти частные производные второго порядка функции
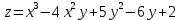 :
:А.
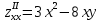 ,
, 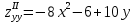 ,
, 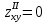 ;
;Б.
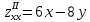 ,
, 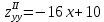 ,
, 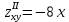 ;
;В.
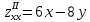 ,
, 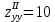 ,
, 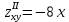 ;
;Г.
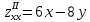 ,
, 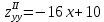 ,
, 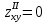 ;
;Д. правильного ответа нет.
8. Найти значение частных производных функции
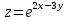 в точке (0,0):
в точке (0,0):А.
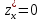 ,
, 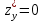 ; Б.
; Б. 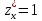 ,
, 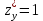 ; В.
; В.  ,
, 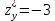 ;
; Г.
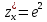 ,
, 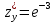 ; Д. правильного ответа нет.
; Д. правильного ответа нет.9. Дана функция
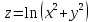 . Чему равно выражение
. Чему равно выражение  в точке (1,1):
в точке (1,1):А. 2; Б. 1; В. 3; Г. Ln2; Д. правильного ответа нет.
10. Вычислить полный дифференциал функции
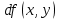 при x=1, y=0
при x=1, y=0
, dx=1/2, dy=1/4, если
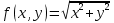 .
.А. ¼; Б. -1/2; В. ½; Г.0; Д. правильного ответа нет.