Файл: Методические указания к выполнению контрольной работы по курсу Спецглавы электроники, для студентов очной и заочной форм обучения.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 04.02.2024

Просмотров: 41

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Курганский государственный университет
Кафедра автоматизации производственных процессов


ПРОЕКТИРОВАНИЕ ЛОГИЧЕСКИХ УСТРОЙСТВ
Методические указания к выполнению контрольной работы

по курсу «Спецглавы электроники»,

для студентов очной и заочной форм обучения

специальностей 15.03.04 – «Автоматизация технологических процессов и производств» и 27.03.04. "Управление в технических системах"

по курсу «Цифровая электроника»,

для студентов заочной форм обучения

специальностей 15.03.04 – «Автоматизация технологических процессов и производств» и 27.03.04. "Управление в технических системах"


Курган 2017
Кафедра автоматизации производственных процессов

Дисциплина: «Спецглавы электроники»

Составил: канд.техн.наук. Б.П. Кудряшов

Утверждено на заседании кафедры « 31 » августа 2017г.

Рекомендовано методическим советом университета « ___» _________ 2017г.
Содержание
Введение 4
Указания к выполнению первой части работы 4
Варианты заданий для выполнения первой части контрольной работы 9
Дополнительные варианты задания 10
Указания к выполнению второй части работы 12
Проектирование счетчиков по произвольному модулю 13
Варианты заданий ко второй части контрольной работы 15
Список рекомендуемой литературы 15

Введение

Целью выполнения контрольной работы является закрепление знаний, полученных на аудиторных занятиях путем самостоятельного выполнения задания по проектированию логических устройств.

В первой части работы студент должен спроектировать комбинационное логическое устройство в соответствии с указанным преподавателем вариантом. Во второй части требуется спроектировать последовательностное логическое устройство также в соответствии с заданным вариантом.

Комбинационными называются логические устройства, в которых в любой момент времени выходные переменные однозначно определяются состоянием входных переменных.

При проектирования комбинационных логических устройств необходимо выполнить и отразить в работе следующие действия:

1.Сформулировать задачу, затем ее формализовать.

2.С помощью карты Карно выполнить минимизацию логического выражения
, реализующего поставленную задачу.

3.Выполнить моделирование работы схемы в программе MULTISIM или ELECTRONICS WORKBENCH (с целью устранения возможных ошибок).

4.Составить принципиальную электрическую схему устройства на заданной серии микросхем.

Указания к выполнению первой части работы

Вначале необходимо ввести буквенные обозначения входных переменных (это могут быть сигналы от датчиков, кнопок управления или выходной код какого-либо цифрового устройства). Затем, на основании анализа требуемых действий разрабатываемого устройства, задать значения выходных переменных (т.е. логических функций) при различных сочетаниях входных переменных. Составить таблицы истинности или внести значения функций в соответствующие клетки карт Карно для всех функций устройства. Если задано логическое выражение в виде ДНФ или КНФ данный пункт опускаем.

Если задана таблица истинности, можно записать СДНФ или СКНФ функции.

СДНФ представляет собой сумму элементарных произведений ( P-термов), в которые входят все входные переменные с инверсиями или без них. В эту сумму входят все элементарные произведения (наборы переменных), на которых функция принимает значение единицы, а переменная записывается без инверсии, если она равна единице и с инверсией, если она равна нулю. Например:

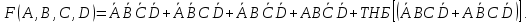
СДНФ функции может быть также записана с помощью номеров термов в сокращенном виде:



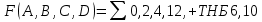
ТНБ - термы не доставляющие беспокойства, (номера наборов переменных), на которых неважно какое значение принимает функция и, таким образом, для них можно задать любое значение функции. В приведенной таблице истинности ТНБ это 6я и 10я строки.


№
A
B
C
D
F

0
0
0
0
0
1

1
0
0
0
1
0

2
0
0
1
0
1

3
0
0
1
1
0

4
0
1
0
0
1

5
0
1
0
1
0

6
0
1
1
0
0/1

7
0
1
1
1
0

8
1
0
0
0
0

9
1
0
0
1
0

10
1
0
1
0
0/1

11
1
0
1
1
0

12
1
1
0
0
1

13
1
1
0
1
0

14
1
1
1
0
0

15
1
1
1
1
0


и карта Карно:


CD

AB
00
01
11
10

00
1






1

01
1






0/1

11
1









10









0/1


СКНФ представляет собой произведение элементарных сумм (S-термов), в которые входят все входные переменные с инверсиями или без них. В эту сумму входят те элементарные суммы, на которых функция принимает значения нуля, а переменная записывается с инверсией, если она равна единице и без инверсии, если она равна нулю:

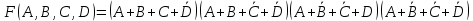
СКНФ функции также может быть записана с помощью номеров термов в сокращенном виде:

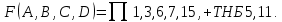
Записи СКНФ, приведенной выше будет соответствовать таблица истинности:

№

A
B
C
D
F

0
0
0
0
0
1

1
0
0
0
1
0

2
0
0
1
0
1

3
0
0
1
1
0

4
0
1
0
0
1

5
0
1
0
1
0/1

6
0
1
1
0
0

7
0
1
1
1
0

8
1
0
0
0
1

9
1
0
0
1
1

10
1
0
1
0
1

11
1
0
1
1
0/1

12
1
1
0
0
1

13
1
1
0
1
1

14
1
1
1
0
1

15
1
1
1
1
0


и карта Карно:


CD
AB
00
01
11
10

00



0
0



01



0/1
0
0

11






0



10






0/1




Минимизация логического выражения позволяет получить схемную конфигурацию устройства, отвечающую заданным условиям, но использующую меньшее количество логических элементов, чем их требуется для реализации устройства по исходному выражению.

Минимизацию логического выражения, описывающего работу устройства можно осуществить с помощью карты Карно:

CD
AB
00
01
11
1 0

00






0



0



01



0/1



0

0

11






0



10






0/1


( )






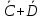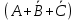
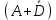
F= ( ) .
Основные правила применения карты Карно:

  1. В контур можно объединять только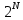 единиц или нулей.

  2. Переменная, изменяющая свое значение в контуре не влияет на функцию и не записывается в выражение для контура.

  3. При объединении единиц выражение для контура записывается как произведение переменных не меняющих свое значение, причем переменная равная единице записывается без инверсии, а равная нулю с инверсией.

  4. При объединении нулей выражение для контура записывается как сумма переменных не меняющих свое значение, причем переменная равная нулю записывается без инверсии, а равная единице с инверсией.

  5. Функция записывается как сумма выражений для контуров (при объединении единиц) или как произведение выражений для контуров (при объединении нулей).

В программах Electronics Workbench и Multisim для минимизации логической функции можно воспользоваться логическим преобразователем (Logic Converter). Инверсия при записи функции показывается апострофом: A’.

В случае если задан тип логических элементов, из которых должна быть собрана схема, минимизированная функция должна быть преобразована к виду, содержащей только заданные логические элементы. Преобразование функции к содержащей только элементы 2И-НЕ или только элементы 2ИЛИ-НЕ можно выполнить используя теорему де Моргана ( 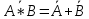, 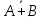= 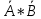) и закон двойного отрицания ( 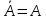). Функцию можно привести к виду содержащей только элементы 2И-НЕ можно также с помощью Logic Converter в программах Electronics Workbench и Multisim.

Моделирование схемы выполнить в программе Electronics Workbench или Multisim, применяя идеальные логические элементы

Смотрите также файлы