Файл: С учётом изложенного выше на поставленные в задаче вопросы можно ответить следующим образом по условию, Р(А)0,5.docx
Добавлен: 04.02.2024
Просмотров: 67
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Задача 1
Малое предприятие имеет два цеха – А и В. Каждому установлен месячный план выпуска продукции. Известно, что цех А свой план выполняет с вероятностью 0,5. Вероятность выполнения плана цехом В при условии, что цех А выполнит свой план, равна 0,4. Известно также, что с вероятностью 0,1 может сложиться ситуация, когда ни один из цехов свой план не выполнит.
Если оба цеха выполнят свои планы в предстоящий месяц, то предприятие увеличит свой счёт в банке на 5 единиц; если оба не выполнят- снимет со счёта 4 единицы; если цех А выполнит, а цех В не выполнит – увеличит счёт только на 2 единицы; если же цех А не выполнит, а цех В выполнит - сократит свой счёт на 1 единицу.
Требуется:
-
определить вероятность выполнения плана цехом В; -
выяснить, зависит ли выполнение плана цехом А от того, выполнит или не выполнит свой план цех В; -
найти вероятность того, что предприятию придётся снимать деньги со счёта в банке; -
определить, на сколько и в какую сторону (увеличения - уменьшения) изменится в среднем счёт предприятия в банке по результатам работы в предстоящем месяце (ожидаемое изменение счёта в банке).
Решение:
Указанные в задаче события полезно представить графически с помощью диаграммы Эйлера-Венна:
О
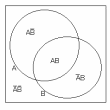
чевидно, что события
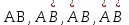 попарно несовместны и образуют полную группу. Кроме того, видно, что справедливы равенства
попарно несовместны и образуют полную группу. Кроме того, видно, что справедливы равенства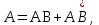

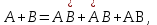
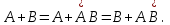
Правые части этих равенств представляют собой суммы опять-таки несовместных событий.
С учётом изложенного выше на поставленные в задаче вопросы можно ответить следующим образом:
-
по условию, Р(А)=0,5;
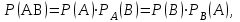 =0,1
=0,1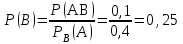
-
Тогда из Р(АВ)=0,1 и ,4
,4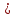 0,25 следует, что
0,25 следует, что 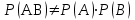 . Это значит, что события А и В являются зависимыми.
. Это значит, что события А и В являются зависимыми.
-
Предприятию придется снимать деньги в банке при условии, что оба банка не выполнят план , и вероятность этого события равна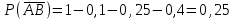 либо цех А не выполнит план, а цех В – выполнит, вероятность этого события равна
либо цех А не выполнит план, а цех В – выполнит, вероятность этого события равна 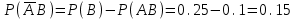
Тогда вероятность снятия денег со счета равна
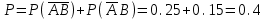
-
Определим, на сколько и в какую сторону (увеличения - уменьшения) изменится в среднем счёт предприятия в банке по результатам работы в предстоящем месяце (ожидаемое изменение счёта в банке).
5-4+2-1=2 ед. – по результатам работы предприятие получит на счет дополнительно 2 единицы.
Задача 2
Оптовая база заключает договоры с магазинами на снабжение товарами. Известно, что от каждого магазина заявка на обслуживание на очередной день может поступить на базу с вероятностью 0,4, причём независимо от других магазинов.

Требуется:
-
определить минимальное количество магазинов (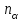 ), с которыми база должна заключить договоры, чтобы с вероятностью не менее
), с которыми база должна заключить договоры, чтобы с вероятностью не менее  от них поступала хотя бы одна заявка на обслуживание на очередной день;
от них поступала хотя бы одна заявка на обслуживание на очередной день; -
при найденном в пункте 1) значении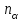 определить:
определить:-
наиболее вероятное число заявок ( ) на обслуживание на очередной день и вероятность поступления такого количества заявок;
) на обслуживание на очередной день и вероятность поступления такого количества заявок; -
вероятность поступления не менее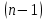 заявок;
заявок; -
математическое ожидание и дисперсию числа заявок на обслуживание на очередной день.
-
Решение:
Анализ условия задачи позволяет сделать вывод о том, что в основу её решения можно положить формулу Бернулли
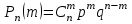
при

-
Минимальный объём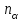 серии испытаний, при котором вероятность наступления события А хотя бы один раз будет не меньше 0,95, определим из условия
серии испытаний, при котором вероятность наступления события А хотя бы один раз будет не меньше 0,95, определим из условия 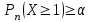 с помощью неравенства
с помощью неравенства
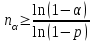 при
при 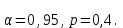
Получим:
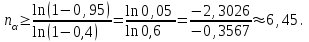
Отсюда
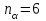
-
Случайная величина Х- число наступлений события А в серии из 6 испытаний, является дискретной с возможными значениями 0; 1; 2;…;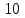 , вероятности которых вычисляются по формуле
, вероятности которых вычисляются по формуле
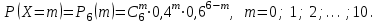
Записанная формула выражает закон распределения вероятностей случайной величины Х. Как известно, этот закон называют биномиальным.
-
Вероятность того, что в данной серии испытаний событие А наступит хотя бы один раз, определим по формуле
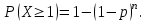
Получим:

-
Для определения вероятности того, что событие А наступит не менее 5 раз, воспользуемся формулой

Вычислим вероятности, стоящие в этом равенстве справа:
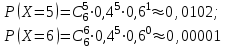
В итоге
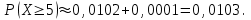
-
Наиболее вероятное значение случайной величины Х найдем из условия
случайной величины Х найдем из условия 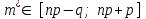 . В нашем случае при
. В нашем случае при 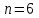 и
и 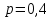 оно принимает вид
оно принимает вид 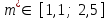 .
.
Отсюда
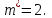 Тогда
Тогда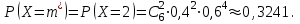
-
Для случайной величины Х , распределённой по биномиальному закону с параметрами и
и 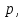 её математическое ожидание и дисперсия определяются по формулам
её математическое ожидание и дисперсия определяются по формулам

При
 и
и  это даёт
это даёт 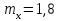 и
и 
Задача 3
В автосалоне ежедневно выставляются на продажу автомобили двух марок – А и В. В течение дня продаётся Х машин марки А и Y машин марки В, причём независимо от того, сколько их было продано в предыдущие дни. Машина марки А стоит 5 ед., машина марки В – 7 ед.
Закон распределения вероятностей системы (Х,Y) задан таблицей
  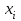 | 0 | 1 | 2 |
| 0 | 0,08 | 0,07 | 0,02 |
| 1 | 0,05 | 0,37 | 0,22 |
| 2 | 0,04 | 0,10 | 0,05 |
Требуется:
-
определить, какая марка машин пользуется в автосалоне наибольшим спросом; -
выяснить, зависит ли число проданных автомашин марки А от числа проданных автомашин марки В; -
найти ожидаемую (среднюю) дневную выручку автосалона; -
оценить (с помощью дисперсии) возможные отклонения дневной выручки относительно среднего значения.
Пояснение: считать, что если P(X >Y) > P(Y >X), то машины марки А
 пользуются большим спросом, чем машины марки В.
пользуются большим спросом, чем машины марки В.-
Определим, какие марки автомобилей пользуются наибольшим спросом:
P(X >Y)=0,05+0,04+0,10=0,19
P(Y >X)=0,07+0,22+0,02=0,31
Условие P(X >Y) > P(Y >X) не выполняется, значит, машины марки В
 пользуются большим спросом, чем машины марки А.
пользуются большим спросом, чем машины марки А.-
Найдём частные распределения вероятностей системы (Х,Y). Возможные значения случайных величин Х и Y прямо указаны в таблице 1, а вероятности этих значений легко вычисляются по формулам
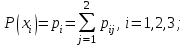
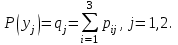
В итоге получаем ряд распределения случайной величины Х:
 |  | 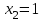 | 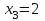 |
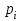 | 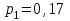 | 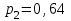 | 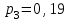 |
и ряд распределения случайной величины Y:
 | 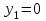 | 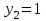 | 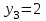 |
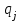 | 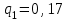 | 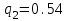 | 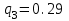 |
Используя полученные данные, определяем числовые характеристики случайных величин Х и Y:
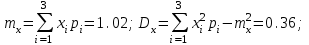
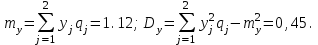
-
Для выяснения вопроса о том, зависимы или нет случайные величины Х и Y, поступим следующим образом. Последовательно, ориентируясь на клетки таблицы 1, вычислим соответствующие произведения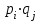 и сравним их с вероятностями
и сравним их с вероятностями  , стоящими в этих клетках: если встретится клетка, для которой
, стоящими в этих клетках: если встретится клетка, для которой 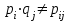 , то сделаем вывод о том , что случайные величины Х и Y являются зависимыми; если же равенство
, то сделаем вывод о том , что случайные величины Х и Y являются зависимыми; если же равенство  выполняется для всех клеток табл.1, то последует вывод о независимости случайных величин Х и Y.
выполняется для всех клеток табл.1, то последует вывод о независимости случайных величин Х и Y.