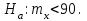Итак, для клетки (1,1): 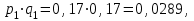но 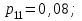следовательно, случайные величины Х и Y зависимы.

4. 
   Корреляционный момент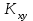 системы (Х,Y) вычислим по формуле 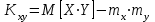. было установлено, что 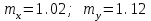. Для нахождения 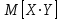используем формулу
   

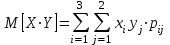
и данные таблицы 1. Получим 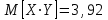. В итоге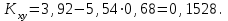

Коэффициент корреляции 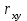определим по формуле

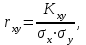где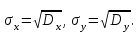

В пункте 1) было установлено, что



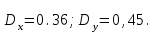
С учётом того, что 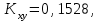находим 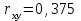. Это значит, что случайные величины Х и Y коррелированны и, следовательно, зависимы (второе подтверждение зависимости).
Задача 4

Торговая фирма располагает разветвлённой сетью филиалов и есть основания считать, что её суммарная дневная выручка Х является нормально распределённой случайной величиной. Наблюдённые значения этой величины по 100 рабочим дням представлены в виде следующего интервального ряда:

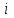	1	2	3	4	5	6	7	8
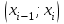	(0;5)	(5;10)	(10;15)	(15;20)	(20;25)	(25;30)	(30;35)	(35;40)
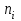	3	5	20	24	22	15	7	4

---

Требуется:

1. 
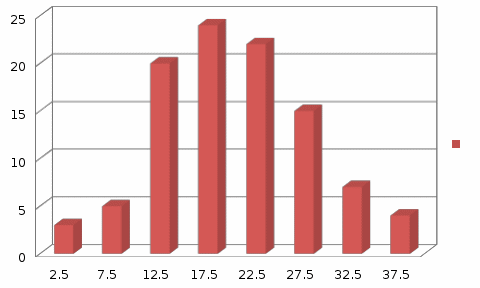
   построить гистограмму относительных частот;
   
2. 
   определить несмещённые оценки для неизвестных математического ожидания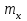 и дисперсии 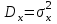случайной величины Х;
   
3. 
   найти 95-процентные доверительные интервалы для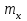 и .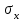
   

Решение:

1 Построим гистограмму относительных частот

Для этого определим середины интервалов

	1	2	3	4	5	6	7	8
	(0;5)	(5;10)	(10;15)	(15;20)	(20;25)	(25;30)	(30;35)	(35;40)
	2,5	7,5	12,5	17,5	22,5	27,5	32,5	37,5
	3	5	20	24	22	15	7	4

2 Определим несмещенные оценки для неизвестных математического ожидания 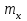и дисперсии 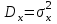случайной величины Х;
3 Доверительный интервал для неизвестного 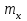имеет вид

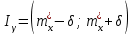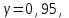, где а .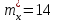

Так как выборка взята из нормальной генеральной совокупности с известным средним квадратическим отклонением, то величина

---

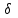определяется по формуле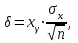



где 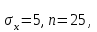а 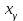есть аргумент функции Лапласа Ф( 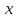), при котором 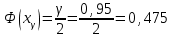. По таблице приложения 2 в [2] находим 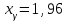. Тогда

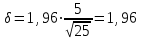и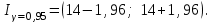

В итоге 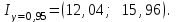Записанный интервал найден по одной реализации выборки и его следует понимать так: он либо содержит, либо не содержит неизвестное математическое ожидание 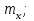однако если получить большое число реализаций выборки объёма 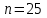из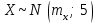



и по каждой реализации найти доверительный интервал, то в среднем 95% найденных интервалов накроют неизвестное . Длины же этих интервалов в данных условиях будут одинаковыми, равными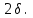

Задача 5
По результатам 18 замеров времени Х изготовления детали определены выборочное среднее 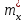=87,17 и исправленная дисперсия 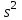=18 . Полагая распределение случайной величины Х нормальным, на уровне значимости = 0,01 решить, можно ли принять 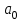=90 в качестве нормативного времени изготовления детали.

Пояснение: Основную гипотезу 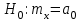проверить при альтернативной гипотезе 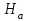, указанной в исходных данных для решения задач.

---

1. 
   
   

2. 
   
   

3. 
   Так как выборка извлечена из нормальной генеральной совокупности с известным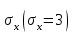 , то в качестве критерия проверки гипотез выберем
   

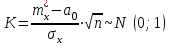
– стандартное нормальное распределение. Заметим, что это имеет место при условии справедливости нулевой гипотезы .

4. 
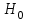   По виду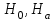 и 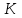заключаем, что критическая область в данном случае будет левосторонней.
   
5. 
   Левую критическую точку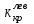 определим так: сначала при уровне значимости 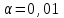из уравнения
   

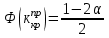
по таблице приложения 2 в [2] найдём 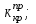после этого положим 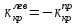. Получим: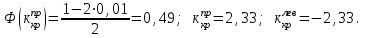

6. 
   Вычислим наблюдаемое значение критерия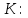
   

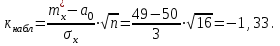
7. 
   Так как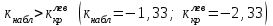 , то нет оснований отвергнуть нулевую гипотезу 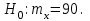Она принимается.
   

---

Смотрите также файлы

• Доклад Чудеса Света.docx

• 175орта мектеп.docx

• Сравнение ФГОС.docx

• азастан Республикасыны Білім жне ылым министрлігі орта мектебі кмм.doc

• Рекомендации к подготовке реферата Реферат.docx