Файл: Лабораторная работа 1 графический интерфейс пользователя и простейшие вычисления цели работы.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.02.2024
Просмотров: 49
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лабораторная работа №1
ГРАФИЧЕСКИЙ ИНТЕРФЕЙС ПОЛЬЗОВАТЕЛЯ И ПРОСТЕЙШИЕ ВЫЧИСЛЕНИЯ
Цели работы:
1. Знакомство с интерфейсом пакета MATLAB и основными положениями.
2. Знакомство с простыми типами данных, вводом данных и визуализацией результата вычислений.
3. Получение практических навыков работы в диалоговом режиме.
4. Работа с комплексными числами и комплексными функциями.
ЗАДАНИЕ 1:
а) вычислить значение функции y =f(x) в точке х0
б) простроить график функции y =f(x) используя встроенную функцию MatLab poly(x,y) на интервале от х0 до хn , шаг аргумента x определить самостоятельно
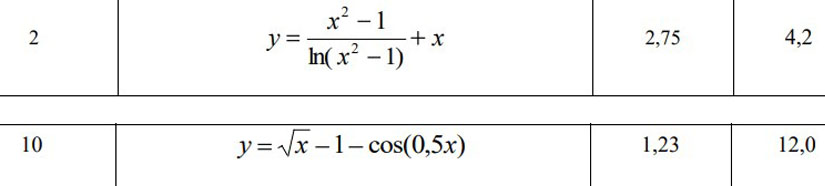
Порядок выполнения задания:
1 написание программы
2 построение графика
3 оформление отчета
Вариант № 2
а)
>> x = 2.75;
>> y = (x^2 - 1)/log(x^2 - 1) + x
y = 6.2381
б)
>> x = 2.75:0.26:4.2;
>> y = (x.^2 - 1)/log(x.^2 - 1) + x
>> plot(x, y)
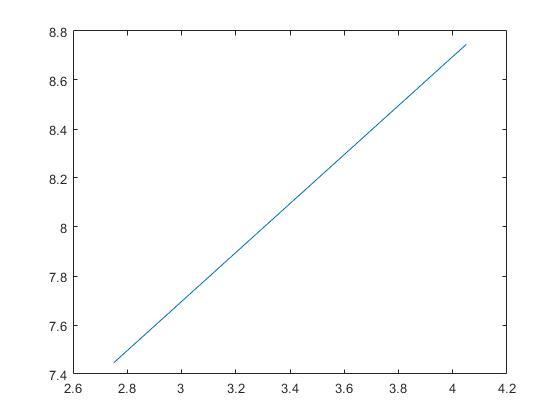
Рисунок 1 График функции y = (x^2 - 1)/log(x^2 - 1) + x
Вариант №10
а)
>> x=1.23;
>> y=sqrt(x)-1-cos(0.5*x)
y = -0.7077
б)
>> x=1.23:0.5:12.0;
>> y=sqrt(x)-1-cos(0.5*x)
y =
Columns 1 through 18
-0.7077 -0.3333 0.0531 0.4479 0.8414 1.2213 1.5744 1.8882 2.1514 2.3557 2.4956 2.5694 2.5789 2.5298 2.4313 2.2951 2.1353 1.9673
Columns 19 through 22
1.8066 1.6684 1.5662 1.5111
>> plot(x,y)
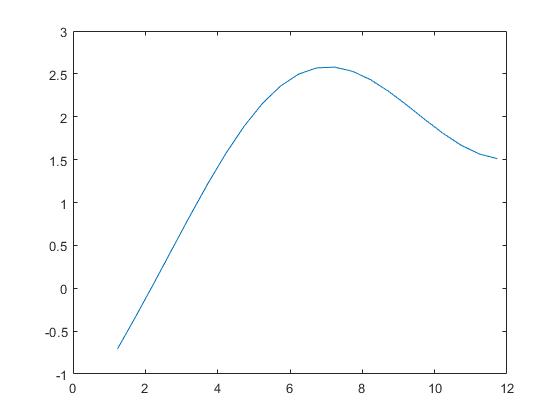
Рисунок 2 График функции y=sqrt(x)-1-cos(0.5*x)
ВЫВОД: В ходе работы было ознакомлено с интерфейсом пакета MATLAB и основными положениями, с простыми типами данных, вводом данных и визуализацией результата вычислений, получение практических навыков работы в диалоговом режиме, ознакомлено работа с комплексными числами и комплексными функциями.
Лабораторная работа № 2
СИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯ В MATLAB
Цели работы:
1. Знакомство с основными положениями пакета символьных вычислений Symbolic Math Toolbox
2. Работа с символьными переменными, матрицами, математическими выражениями.
3. Освоение символьных аналитических вычислений – упрощение выражений, решение алгебраических уравнений, решение системы линейных уравнений, вычисление суммы ряда.
4. Освоение символьного интегрирования и символьного дифференцирования.
5. Получение практических навыков работы в диалоговом режиме.
ЗАДАНИЕ 1:
Решить алгебраические уравнения, используя команду solve: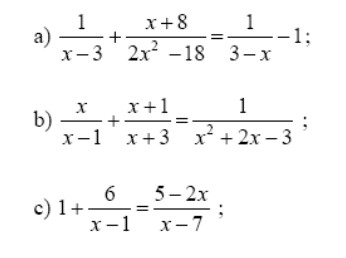
Вариант №А
x = sym('x')
solve(1/(x-3)+(x + 8)/(2*x^2 - 18) == 1/(3-x) - 1)
x =
x
ans =-2 -1/2
Вариант №Б
x = sym('x')
solve(x/(x-1)+(x+1)/(x+3)==1/(x^2+2*x-3))
x =
x
ans = -2 ½
Вариант №С
x = sym('x')
solve(1+6/(x-1)==(5-2*x)/(x-7))
x =
x
ans = -2 5
ЗАДАНИЕ 2:
Решить систему алгебраических уравнений, используя команду solve. Выбрать уравнение согласно своему варианту.
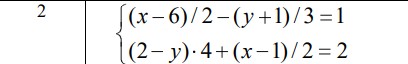

Вариант 2
syms x y
>> [Sx, Sy] = solve((x - 6)/2 - (y + 1)/3 == 1, (2 - y)*4 + (x - 1)/2 == 2)
Sx =
115/11
Sy = 59/22
Вариант 15
>> syms x y
[Sx, Sy] = solve(x+y==3, x^2+3*x*y+y^3-x-y==2)
Sx =
3 - root(z^3 - 2*z^2 + 3*z + 4, z, 1)
3 - root(z^3 - 2*z^2 + 3*z + 4, z, 2)
3 - root(z^3 - 2*z^2 + 3*z + 4, z, 3)
Sy =
root(z^3 - 2*z^2 + 3*z + 4, z, 1)
root(z^3 - 2*z^2 + 3*z + 4, z, 2)
root(z^3 - 2*z^2 + 3*z + 4, z, 3)
ЗАДАНИЕ 3:
Упростить выражения, используя команду simplify:
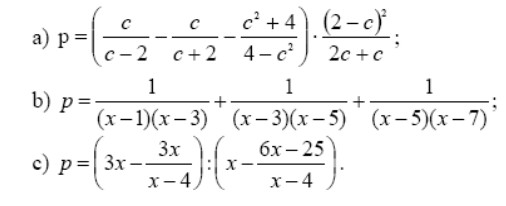
Вариант №А
>> syms p c
>> simplify(p == ((c/(c - 2) - c/(c + 2) - (c^2 + 4)/(4 - c^2))*((2 - c)^2/(2*c + c))))
ans =
3*c*p == c^2 – 4
Вариант №Б
>> syms p c
simplify(p == ((1/((x-1)*(x-3))+1/((x-3)*(x-5))+1/((x-5)*(x-7)))))
ans =x
= 3 & x
= 5 & 3*x^2 - 24*x + 45 == p*(x - 1)*(x - 3)*(x - 5)*(x - 7)
Вариант №С
syms p c
simplify(p == (((3*x-3*x/(x-4))/(x-(6*x-25)/(x-4)))))
ans =25*p + 3*x - 10*p*x + p*x^2 == 3*x*(x - 4) & x
= 5
Лабораторная работа №1
ГРАФИЧЕСКИЙ ИНТЕРФЕЙС ПОЛЬЗОВАТЕЛЯ И ПРОСТЕЙШИЕ ВЫЧИСЛЕНИЯ
Цели работы:
1. Знакомство с интерфейсом пакета MATLAB и основными положениями.
2. Знакомство с простыми типами данных, вводом данных и визуализацией результата вычислений.
3. Получение практических навыков работы в диалоговом режиме.
4. Работа с комплексными числами и комплексными функциями.
ЗАДАНИЕ 1:
а) вычислить значение функции y =f(x) в точке х0
б) простроить график функции y =f(x) используя встроенную функцию MatLab poly(x,y) на интервале от х0 до хn , шаг аргумента x определить самостоятельно
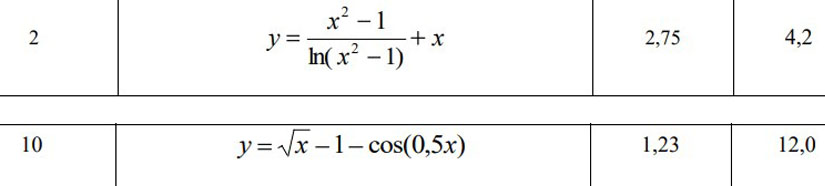
Порядок выполнения задания:
1 написание программы
2 построение графика
3 оформление отчета
Вариант № 2
а)
>> x = 2.75;
>> y = (x^2 - 1)/log(x^2 - 1) + x
y = 6.2381
б)
>> x = 2.75:0.26:4.2;
>> y = (x.^2 - 1)/log(x.^2 - 1) + x
>> plot(x, y)

Рисунок 1 График функции y = (x^2 - 1)/log(x^2 - 1) + x
Вариант №10
а)
>> x=1.23;
>> y=sqrt(x)-1-cos(0.5*x)
y = -0.7077
б)
>> x=1.23:0.5:12.0;
>> y=sqrt(x)-1-cos(0.5*x)
y =
Columns 1 through 18
-0.7077 -0.3333 0.0531 0.4479 0.8414 1.2213 1.5744 1.8882 2.1514 2.3557 2.4956 2.5694 2.5789 2.5298 2.4313 2.2951 2.1353 1.9673
Columns 19 through 22
1.8066 1.6684 1.5662 1.5111
>> plot(x,y)

Рисунок 2 График функции y=sqrt(x)-1-cos(0.5*x)
ВЫВОД: В ходе работы было ознакомлено с интерфейсом пакета MATLAB и основными положениями, с простыми типами данных, вводом данных и визуализацией результата вычислений, получение практических навыков работы в диалоговом режиме, ознакомлено работа с комплексными числами и комплексными функциями.
Лабораторная работа № 2
СИМВОЛЬНЫЕ ВЫЧИСЛЕНИЯ В MATLAB
Цели работы:
1. Знакомство с основными положениями пакета символьных вычислений Symbolic Math Toolbox
2. Работа с символьными переменными, матрицами, математическими выражениями.
3. Освоение символьных аналитических вычислений – упрощение выражений, решение алгебраических уравнений, решение системы линейных уравнений, вычисление суммы ряда.
4. Освоение символьного интегрирования и символьного дифференцирования.
5. Получение практических навыков работы в диалоговом режиме.
ЗАДАНИЕ 1:
Решить алгебраические уравнения, используя команду solve: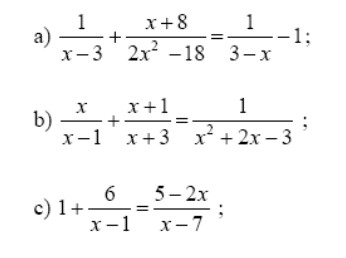
Вариант №А
x = sym('x')
solve(1/(x-3)+(x + 8)/(2*x^2 - 18) == 1/(3-x) - 1)
x =
x
ans =-2 -1/2
Вариант №Б
x = sym('x')
solve(x/(x-1)+(x+1)/(x+3)==1/(x^2+2*x-3))
x =
x
ans = -2 ½
Вариант №С
x = sym('x')
solve(1+6/(x-1)==(5-2*x)/(x-7))
x =
x
ans = -2 5
ЗАДАНИЕ 2:
Решить систему алгебраических уравнений, используя команду solve. Выбрать уравнение согласно своему варианту.
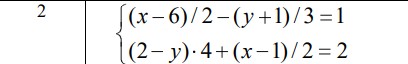

Вариант 2
syms x y
>> [Sx, Sy] = solve((x - 6)/2 - (y + 1)/3 == 1, (2 - y)*4 + (x - 1)/2 == 2)
Sx =
115/11
Sy = 59/22
Вариант 15
>> syms x y
[Sx, Sy] = solve(x+y==3, x^2+3*x*y+y^3-x-y==2)
Sx =
3 - root(z^3 - 2*z^2 + 3*z + 4, z, 1)
3 - root(z^3 - 2*z^2 + 3*z + 4, z, 2)
3 - root(z^3 - 2*z^2 + 3*z + 4, z, 3)
Sy =
root(z^3 - 2*z^2 + 3*z + 4, z, 1)
root(z^3 - 2*z^2 + 3*z + 4, z, 2)
root(z^3 - 2*z^2 + 3*z + 4, z, 3)
ЗАДАНИЕ 3:
Упростить выражения, используя команду simplify:
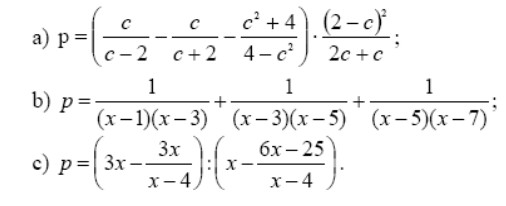
Вариант №А
>> syms p c
>> simplify(p == ((c/(c - 2) - c/(c + 2) - (c^2 + 4)/(4 - c^2))*((2 - c)^2/(2*c + c))))
ans =
3*c*p == c^2 – 4
Вариант №Б
>> syms p c
simplify(p == ((1/((x-1)*(x-3))+1/((x-3)*(x-5))+1/((x-5)*(x-7)))))
ans =x
= 3 & x ЗАДАНИЕ 4:
Вычислить сумму ряда, используя команду symsum. Выбрать уравнение согласно своему варианту.
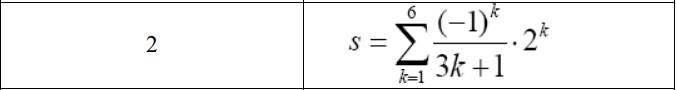
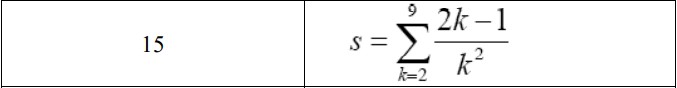
Вариант №2
syms s k n
[s] = symsum((-1)^k/(3*k + 1)*(2^k), 1, 6)
s =32343/17290
Вариант №15
syms s k n
[s] = symsum(((2*k-1)/k^2),2,9)
s =19801619/6350400
ЗАДАНИЕ 5:
Вычислить производную функции по х, используя команду diff. Выбрать функцию согласно своему варианту.
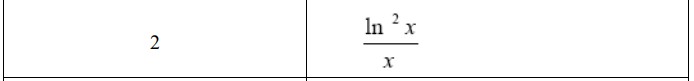

Вариант №2
>> syms x
>> diff(log(x).^2/x)
ans =(2*log(x))/x^2 - log(x)^2/x^2
Вариант №15
syms x
diff(x/(x^4+3*x^2+2))
ЗАДАНИЕ 6:
Используя функцию int, подготовить и организовать вычисление определенного интеграла: Подынтегральная функция f(x) определена и непрерывна на интервале a <= x <= b. Вид подынтегральной функции f(x), а также интервал интегрирования [a, b] определяется номером варианта


Вариант №2
syms x
>> int(log(x).^2/x,1,4)
ans =
log(4)^3/3
Вариант №15
syms x
int(x/(x^4+3*x^2+2),1,2)
ans =log(5^(1/2)/2)
ВЫВОД: В ходе работы было ознакомлено с основными положениями пакета символьных вычислений Symbolic Math Toolbox, работа с символьными переменными, матрицами, математическими выражениями, освоение символьных аналитических вычислений – упрощение выражений, решение алгебраических уравнений, решение системы линейных уравнений, вычисление суммы ряда, освоение символьного интегрирования и символьного дифференцирования, получение практических навыков работы в диалоговом режиме.
Лабораторная работа №3
ВЫСОКОУРОВНЕВАЯ ГРАФИКА MATLAB
Цели работы:
1. Знакомство с основными возможностями высокоуровневой (high-level) графики MATLAB для отображения функций двух и трѐх переменных, визуализации векторных и матричных данных и векторных полей.

ЗАДАНИЕ 1
Вариант №1
>> x = -10:1/100:10;
y = x.^2-4;
plot(x,y)
Вариант №2
x = -10:1/100:10;
y = x.^4 - 4*x.^2 ;
plot(x,y)
Вариант №3
>> x = -10:1/100:10;
y = sin(x) + log(x);
plot(x,y)
ЗАДАНИЕ 2
Вариант №1
>> t = -pi:0.1:pi; x = t - sin (t);
y = 1- cos (t);
plot(x,y)
title('Параметрическая функция x = t - sin (t) y = 1- cos (t) ')
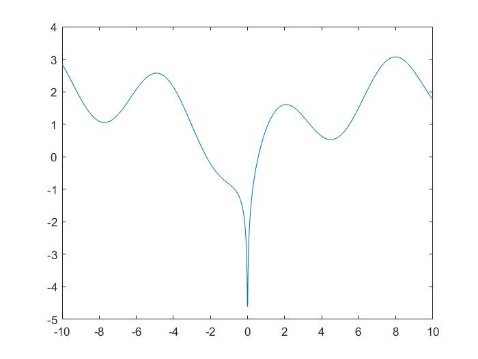
Рисунок 3 График функции
Вариант №2
t = 0:0.1:2*pi;
x = t - sin (t);
y = 1- cos (t);
plot(x,y)
title('Параметрическая функция x = t - sin (t) y = 1- cos (t) ')
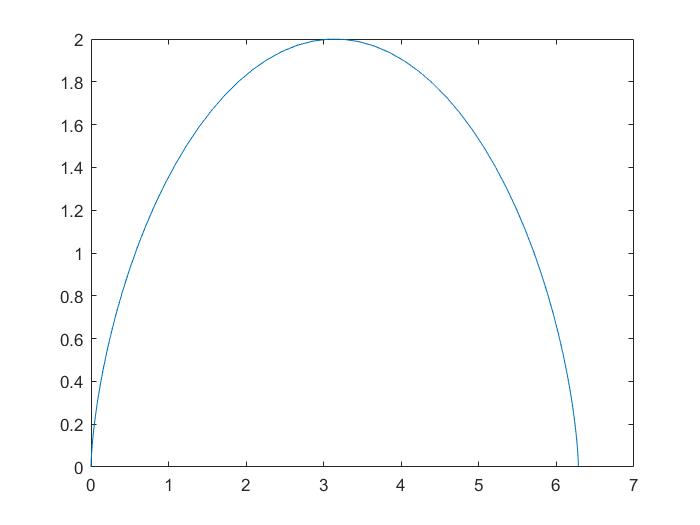
Рисунок 4 График функции
ЗАДАНИЕ 3
Вариант №1
r = 0:1/100:2*pi;
r = 1 + sin (t);
polar(r)
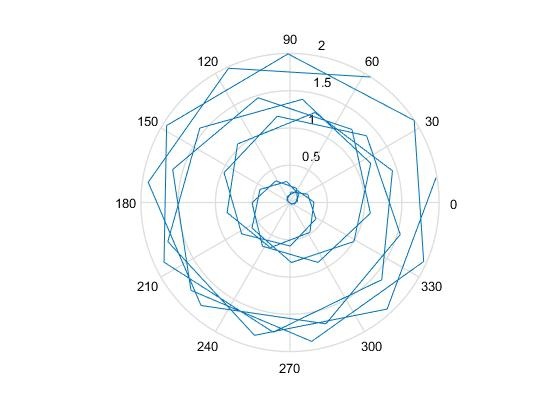
Рисунок 5 График функции
Вариант №2
r = 0:1/100:2*pi;
r = 1 + cos(2*t);
polar(r)
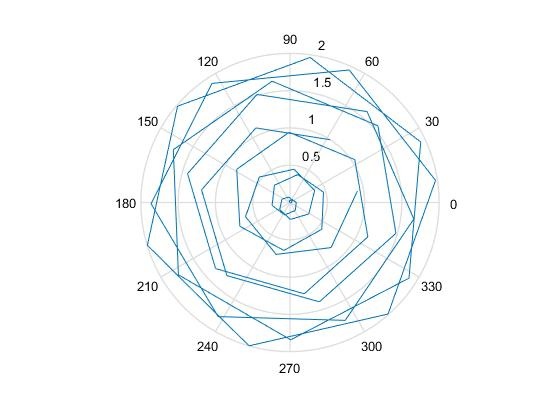
Рисунок 6 График функции
ЗАДАНИЕ 4
Вариант №1
[x, y] = meshgrid(-1:0.05:1, 0:0.05:1);
z = sqrt(abs(x))-sqrt(abs(y));
mesh(x, y, z)
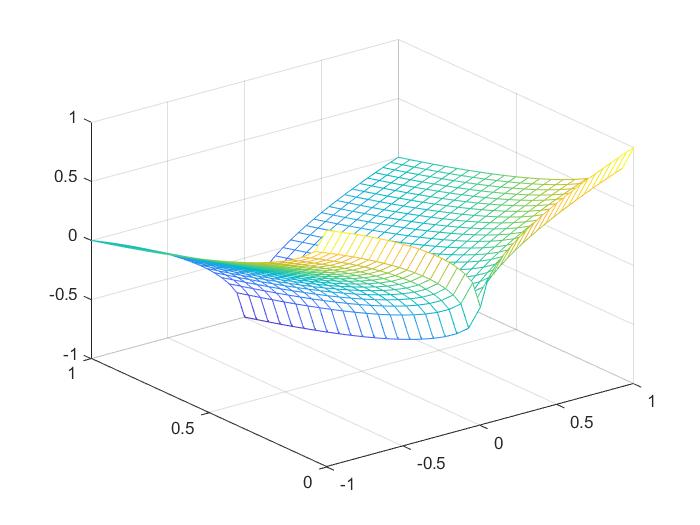
Рисунок 7 График функции
Вариант №2
[x, y] = meshgrid(-1:0.05:1, 0:0.05:1);
z = y.^2-x.^2;
mesh(x, y, z)

Рисунок 8 График функции
Вывод:
Мы узали основные возможности высокоуровневой (high-level) графики MATLAB для отображения функций двух и трёх переменных, визуализации векторных и матричных данных и векторных полей.
Лабораторная работа № 4.
МЕТОДЫ ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ.
Цель:
Целью лабораторной работы является изучение простых приемов языка программирования среды MatLAB. Основной задачей ставится изучение типовых конструкций языка, таких как функции, условия и циклы..
ЗАДАНИЕ 1:
Создать m-файл, вычисляющий значения функции f(x) на отрезке [-1; 0.1] с шагом h 0,1.. Построить график этой функции с помощью процедуры fplot в границах, заданных в задании. Вычислите интеграл от функции в тех же пределах, используя встроенные функции. Найдите экстремумы и ближайший корень (нуль) функции.
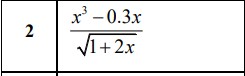
Задаём функцию
function [y] = Fun331(x)
y = ((x.^3-0.3.*x)/sqrt(1+2.*x));
окно
fplot('Fun331', [-1 0], 0.1),grid

Рисунок 9 Полученный график
-------------------------------
интеграл
>> x= -1:0.1:0;
>> y = @Fun331
y = function_handle with value:
@Fun331
>> J1 = trapz(x)
J1 = -5
------------
>> x=-1:0.1:0; /////ближайший мин
y = (cos (pi*x.^2))/(sqrt(1-3*x));
plot(x,y,'-k'), grid
>>
>> y=Fun314(x);
Undefined function or variable 'Fun314'.
Did you mean:
>> y=Fun331(x);
>> [xmin,ymin]=fminsearch(@Fun331,-1)
xmin = -0.9903
ymin = -0.5009
>> y=Fun331(x);
>> [xmin,ymin]=fminsearch(@Fun331,0)
xmin = -0.9903
ymin = -0.5009
>>
-----------------------------------------------
[y,fval] = fminsearch(@(x) ((cos (pi*x.^2))/(sqrt(1-3*x))), [-1,0]) \\\\\\\ экстремум
Exiting: Maximum number of function evaluations has been exceeded
- increase MaxFunEvals option.
Current function value: -0.416387
y = -1.0223 0.3068
fval = -0.4164
>>
-------------------
fplot('Fun332', [2 4], 0.2),grid
function [y] = Fun332(x)
y = sqrt(3*x.^2+5)*sin((3*x)/2)
end
Вывод: Нами были изучены простые приёмы языка программирования MatLab.
Лабораторная работа № 5
МЕТОДЫ ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ
Цель работы:
1. Изучить Curve Fitting Toolbox
ЗАДАНИЕ 1:
1.Получить у преподавателя файл с исходными данными (.txt, xls)
2. Выполнить операцию экспорта исходных данных в глобальные массивы (вектора) рабочей среды MATLAB.
3. В приложении cftool выполнить приближение данных, при помощи параметрических моделей из библиотеки моделей, или заданных пользователем.
4. Произвести качественную и количественную оценку пригодности выполненного приближения.
5. В отчете о выполненной работе должны быть приведены результаты минимум четырех вариантов приближения

Рисунок 10 Макет графика
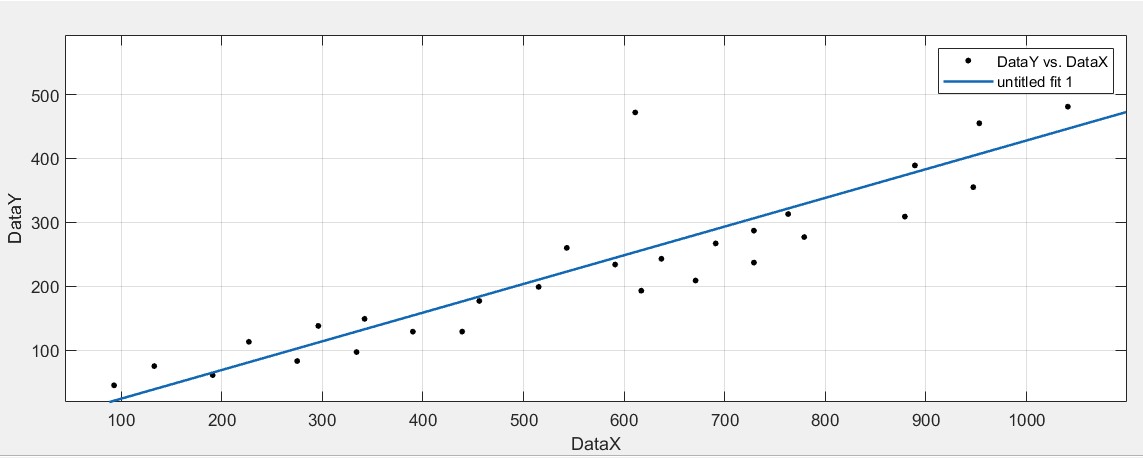
Рисунок 11 График построенный с помощью Polynomial
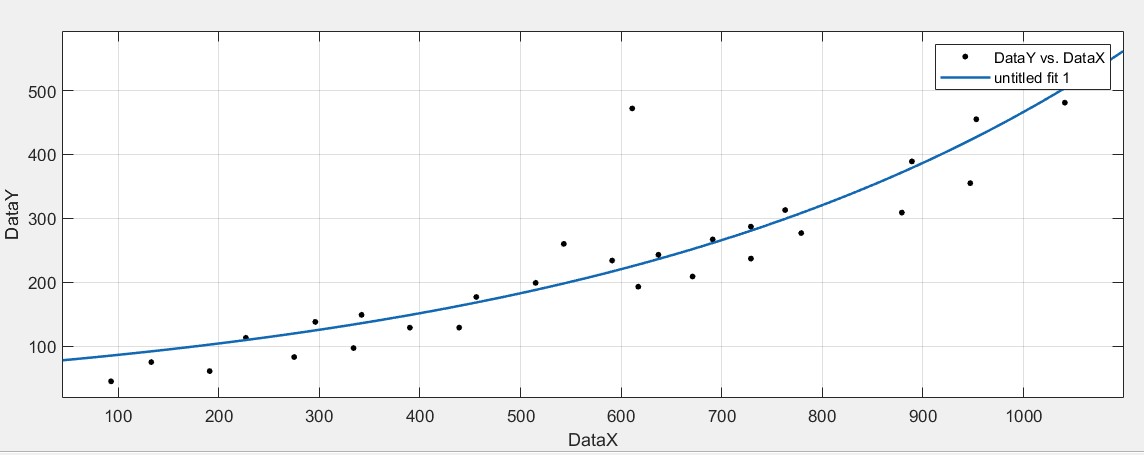
Рисунок 12 График построенный с помощью Exponential
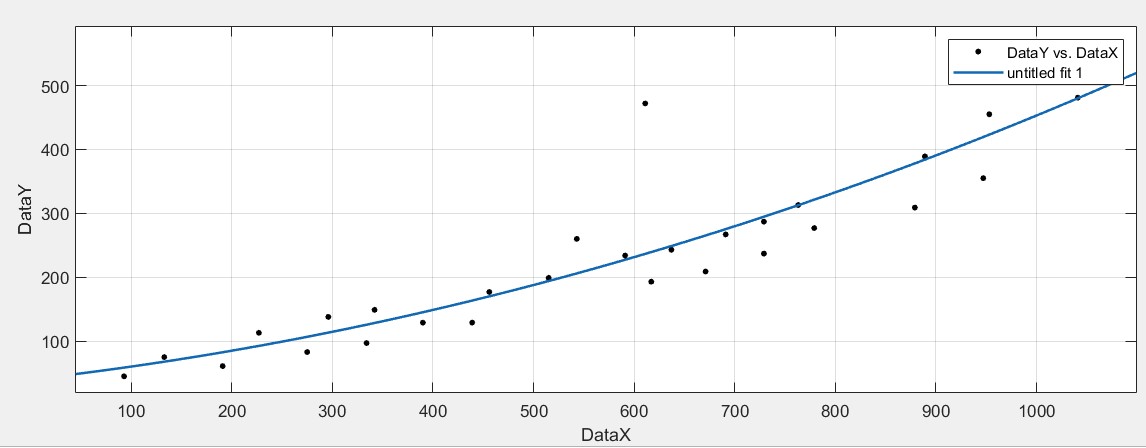
Рисунок 13 График построенный с помощью Fourier
Вывод:
При проверке создания графика различными методами в MatLab. Был выявлен наиболее качественный метод построения графика, Fourier.