Файл: Государственное казенное общеобразовательное учреждение Свердловской области Тавдинская вечерняя школа. Проектноисследовательская работа.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.02.2024
Просмотров: 38
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Государственное казенное общеобразовательное учреждение
Свердловской области «Тавдинская вечерняя школа».
Проектно-исследовательская работа:
"Удивительные фигуры: правильные многогранники".
Авторы:
Новокрещенов Виктор, Безумов Сергей учащийся 11 класса
Руководитель:
Изюменко Т.А. учитель математики
г. Тавда 2019 г.
Краткая аннотация.
В этом году на внеклассных занятиях по математике мы изучали правильные многогранники, которые называют ещё Платоновыми телами. Изготавливая их модели, мы были удивлены необычностью и красотой некоторых из них. С помощью развёрток мы научились конструировать эти фигуры. Но для того, чтобы построить развёртку нужно обладать комплексом математических знаний, чертёжными навыками, пространственным мышлением.
Мы решили больше узнать о правильных многогранниках, познакомиться с историей их появления, научиться их строить оптимально, легко и быстро, исследовать их роль в окружающем мире, и, наконец, разобраться, а пригодятся ли нам эти фигуры и знания о них в практической жизни
Цель исследования: расширение круга знаний о правильных многогранниках, изучение практического применения в окружающем мире.
Задачи исследования:
- изучить информационные источники по данной теме;
- изготовить коллекцию правильных многогранников и отследить интерес к ним.
- найти примеры правильных многогранников в окружающей природе и в бытовой среде;
- доказать, что формы правильных многогранников применимы в быту.
Объект исследования: правильные многогранники.
Предмет исследования: значение и применение этих фигур
Методы исследования:
- поиск, сбор и обработка информации по теме; наблюдение; анкетирование; практическая работа.
Работая над этой темой мы выполнили все цели и задачи, которые ставили перед собой: научились конструировать модели правильных многогранников, изучили историю возникновения
, их свойства, нашли связь форм правильных многогранников с природными объектами, нашли применение в повседневной жизни. Мы убедились, что эти фигуры вызывают интерес у окружающих. Кроме этого мы научились решать некоторые математические задачи, с помощью циркуля и линейки, совершенствуя тем самым свои чертёжные навыки и математические знания. Это очень нам пригодится, т.к. уже в следующем году нам предстоит сдавать экзамены.
В результате практической работы, мы совершенствовали мелкую моторику рук, у нас развивались фантазия и воображение, трудолюбие и настойчивость в достижении поставленных целей.
Оглавление.
-
Введение. 3 -
Понятие правильного многогранника 4-5 -
Из истории многогранников 5-6 -
Использование форм и применение правильных многогранников 7-8 -
Изготовление правильных многогранников 8-11 -
Опрос и публикация в СМИ 12 -
Заключение. 12 -
Список источников информации. 13 -
Приложения 14-18
Введение
В нашем мире много необычного и прекрасного. Нас окружают предметы, формы которых нас удивляют. Таковыми, например, являются правильные многогранники. Эти фигуры обладают и красотой, и совершенностью форм, и притягательностью.
С раннего детства мы уже встречаемся с правильными многогранниками, играя в кубики и развивающие конструкторы, решая головоломки Кубика-Рубика и его разновидностей. Архитекторы, строители и дизайнеры воплощают свои оригинальные идеи, используя эти фигуры.
В этом году на занятиях по математике мы изучали правильные многогранники, которые называют ещё Платоновыми телами. В учебных пособиях по геометрии за курс средней школы даны очень не богатые сведения о многогранниках. Задач на эту тему предлагается совсем немного, из-за чего возможности темы совершенно не раскрываются. А ведь она в теоретическом отношении очень богата, позволяет сформулировать много интересных задач. Решение предложенных задач позволит увидеть, что определенные приемы построения помогают в значительной мере упростить как само построение, так и понимание свойств фигуры.
Изучая свойства этих фигур, конструируя их развёртки, складывая многогранники, мы поняли, что нам это интересно. Мы решили больше узнать о правильных многогранниках, познакомиться с историей их появления, исследовать их роль в окружающем мире, и найти их практическое применение.
Гипотеза: правильные многогранники – гармоничные и выгодные фигуры и их можно широко использовать.
Цель исследования: расширение круга знаний о правильных многогранниках, изучение практического применения в окружающем мире.
Задачи исследования:
- изучить литературные источники по данной теме;
- изготовить коллекцию правильных многогранников и отследить интерес к ним.
-найти примеры правильных многогранников в окружающей природе и в бытовой среде;
-доказать, что формы правильных многогранников применимы в быту.
Объект исследования: правильные многогранники.
Предмет исследования: значение и применение этих фигур
Методы исследования:
- поиск, сбор и обработка информации по теме
- наблюдение;
- практическая работа.
- анкетирование;
Понятие правильного многогранника.
Многогранники - это простейшие фигуры в пространстве, как, например, многоугольники - простейшие фигуры на плоскости. Если рассматривать многогранник с точки зрения геометрии, то это часть пространства, ограниченная плоскими многоугольниками, называемыми гранями. Стороны и вершины граней называют рёбрами и вершинами самого многогранника.
Правильный многогранник это фигура, обладающая следующими свойствами:
- он выпуклый;
- все его грани являются равными правильными многоугольниками;
- в каждой его вершине сходится одинаковое число граней;
- все его двугранные углы равны.
Доказано существование только пяти правильных многогранников.
| Тетраэдр составлен из четырёх равносторонних треугольников. Каждая его вершина является вершиной трёх треугольников. |  |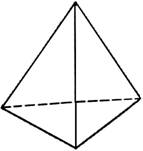
| Куб (гексаэдр) составлен из шести квадратов. Каждая вершина куба является вершиной трёх квадратов. |  |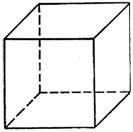
| Октаэдр составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырёх треугольников. |  |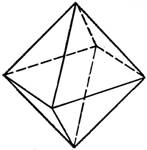
| Додекаэдр составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. |  |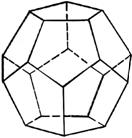
| Икосаэдр составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. |  |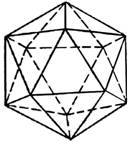
Названия этих фигур запомнить очень легко. (Приложение 1)
В переводе с греческого «эдра» означает грань,
«тетра» - 4,
«гекса» - 6,
«окта» - 8,
«додека» - 12,
«икоса» - 20.
Основными характеристиками многогранника являются число и вид граней, число вершин и число ребер. Эти характеристики для правильных многогранников представлены в таблице (Приложение 2)
Изучив внимательно содержание таблицы, мы увидели закономерность: если число ребер рассматриваемого многогранника увеличить на 2, то получится число, равное сумме числа граней и вершин этого многогранника.
Сформулируем это правило так: « Сумма числа граней и вершин равна числу рёбер, увеличенному на 2», то есть Г + В = Р + 2 .
| Правильный многогранник | ЧИСЛО ГРАНЕЙ + ВЕРШИН | ЧИСЛО РЕБЕР |
| ТЕТРАЭДР | 4 + 4 = 8 | 6 |
| КУБ | 6 + 8 = 14 | 12 |
| ОКТАЭДР | 8 + 6 = 14 | 12 |
| ДОДЕКАЭДР | 12 + 20 = 32 | 30 |
| ИКОСАЭДР | 20 + 12 = 32 | 30 |
Таким образом, мы открыли формулу, которая впервые была выведена Рене Декартом в 1640 году, а позднее вновь открыта Эйлером в 1752 году, имя которого с тех пор она и носит. Формула Эйлера верна для любых выпуклых многогранников.
Из истории многогранников.
| О правильных многогранниках человечество знает давно. Их орнаментные модели можно найти на резных шарах из камней, появившихся в Шотландии, задолго до того, как их открыл Платон. Разновидные игральные кости того времени, также по форме напоминают правильные многогранники. |
 |
| Уже тогда люди использовали бронзовые аналоги этих удивительных фигур.    |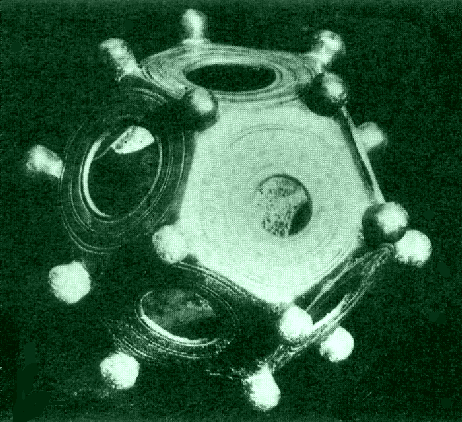
Честь открытия и детального изучения правильных многогранников приписывают древнегреческим учёным. В некоторых источниках можно найти информацию о том, что Пифагор впервые выделил эти фигуры. В других источниках утверждается, что ему были знакомы только тетраэдр, куб и додекаэдр, а октаэдр и икосаэдр открыл Теэтет Афинский, который ещё описал все пять правильных многогранников.
Значительное внимание правильным многогранникам уделял Платон, в честь которого они и названы «Платоновы тела».
Он каждой из четырёх стихий Земле, Воздуху, Воде и Огню сопоставил определённый правильный многогранник.
Куб или Гексаэдр предназначался Земле,
Октаэдр - Воздуху,
Икосаэдр - Воде,
а Тетраэдр - Огню.
Такое сопоставление очень легко объяснить: жар огня ощущается чётко и остро как маленькие тетраэдры; воздух состоит из октаэдров: его мельчайшие компоненты настолько гладкие, как капельки воды, на которые больше всего похожи икосаэдры; в противоположность воде, устойчивые кубики составляют землю. По поводу пятого элемента, додекаэдра, Платон писал: «…его бог определил для Вселенной и прибегнул к нему в качестве образца».
Полное математическое описание пяти правильных многогранников дал Евклид и доказал, что других правильных многогранников нет.
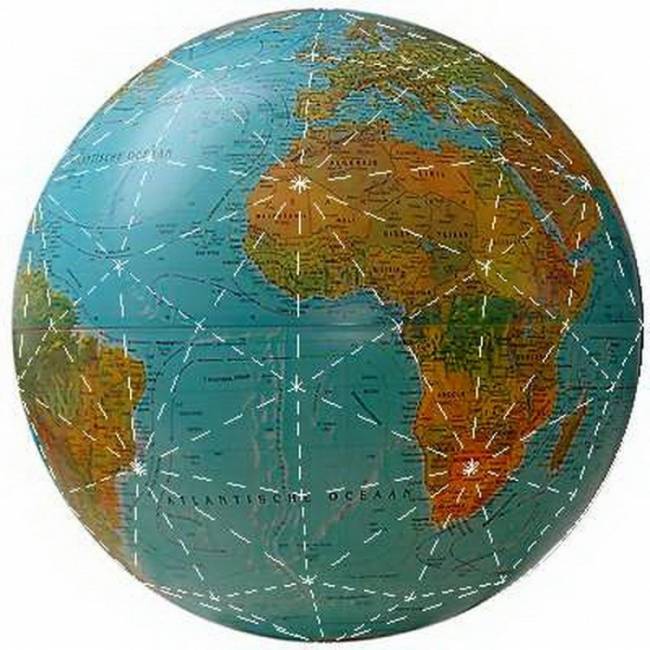Идеи Платона о связи правильных многогранников с гармоничным устройством мира нашли своё продолжение и в наше время. В 80-х годах. московские инженеры В. Макаров и В. Морозов высказали интересную научную гипотезу: ядро Земли имеет форму и свойства растущего кристалла, которое оказывает активное воздействие природные процессы, идущие на планете. Силовое поле лучей этого кристалла, формируют икосаэдро-додекаэдровую структуру Земли. Она проявляется в том, что в земной коре как бы проступают проекции вписанных в земной шар правильных многогранников: икосаэдра и додекаэдра.Доказано, что многие залежи полезных ископаемых как раз и находятся вдоль икосаэдро-додекаэдровой сетки: 62 вершины и середины рёбер многогранников, обладают особыми свойствами, позволяющими объяснить многие явления на нашей планете. Здесь располагаются очаги древнейших культур и цивилизаций: Перу, Северная Монголия, Гаити, Обская культура и другие. В этих точках наблюдаются максимумы и минимумы атмосферного давления, гигантские завихрения Мирового океана. В этих узлах находятся озеро Лох-Несс, Бермудский треугольник.