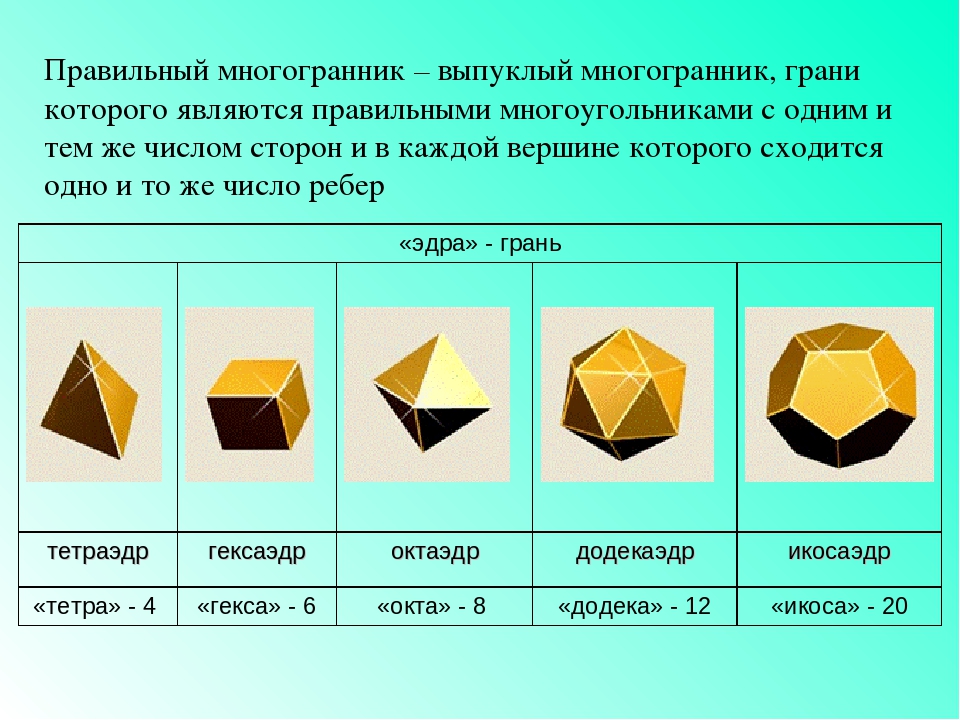
Использование форм и применение правильных многогранников.

Правильные многогранники – самые выгодные фигуры. Человек и природа этим широко пользуются. Подтверждением тому служит форма некоторых кристаллов. Например, кристаллы поваренной соли имеют форму куба.

А как разнообразен мир кристаллов, являющихся природными многогранниками. Мы живём в мире кристаллов: ходим по кри­сталлам, строим из кристаллов, обрабатываем кристаллы на заводах, выращиваем кристаллы в лабораториях, создаем приборы и изделия из кристаллов, широко применяем кристаллы в науке и технике, едим кри­сталлы, лечимся кристаллами. Рассматривая кристаллы горного хрусталя и кварца, можно заметить что, они имеют шестиугольную призматическую поверхность. Этот минерал обладает целебными свойствами. Раньше маленьким детям этот камень вешали на грудь, повязывая его на верёвочку, чтобы рёбёнок не простудился и не страдал простудой. Ещё мы убедились, что кристаллы калийной соли имеют форму гексаэдра. Этот минерал используют при изготовлении минеральных удобрений.

Много разных бактерий и вирусов имеют форму многогранников. 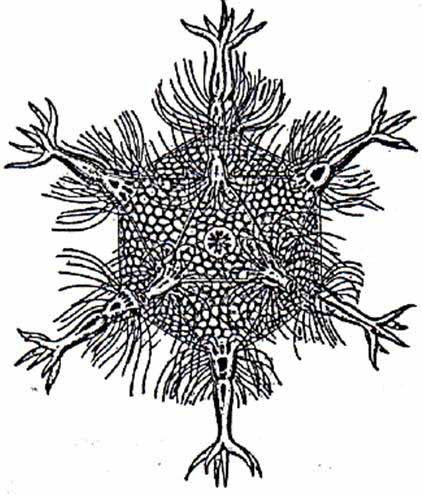Но все они имеют икосаэдровую или додекаэдровую форму. Например, скелет одноклеточного организма феодарии по форме напоминает икосаэдр.

Из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объём при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи.

Большинство феодарий живут на морской глубине и служат добычей коралловых рыбок. Но простейшее животное защищает себя иглами, выходящими из вершин скелета. Так оно больше похоже на звёздчатый многогранник.

Гармоничность и простота правильных многогранников позволила создать серию игрушек, головоломок и конструкторов. Играя в эти игрушки, у нас развивается логическое мышление, воображение, совершенствуется и мелкая моторика рук.

На уроке творчества, прежде чем чертить развёртку и склеивать многогранник из бумаги, мы собирали правильный многогранник с помощью стереометрического ящика.

---

Формы правильных многогранников также используются в бытовых предметах и упаковке товаров: чайные и молочные пакеты, коробочки и различные сувениры и др. . (Приложение 3)

А какие необычные и смелые идеи воплощают архитекторы, строители и дизайнеры с помощью форм правильных многогранников. В интернете мы нашли очень много фотографий как эти удивительные фигуры используются при строительстве зданий, оформлении парков и дизайне бытовых интерьерных решений. (Приложение 4)
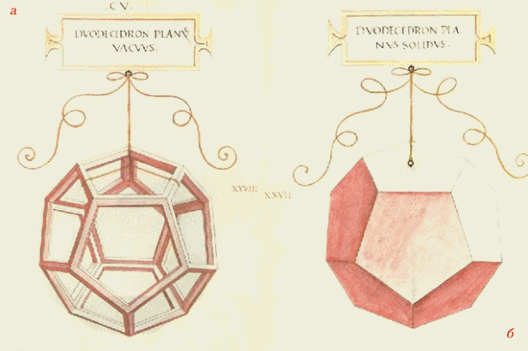
Художники разных эпох проявляли постоянный интерес к изучению и изображению многогранников. Пик этого интереса приходится, конечно, на эпоху Возрождения. Изучая явления природы, художники стремились найти обоснованные с точки зрения науки способы их изображения. Учения о перспективе, светотени и пропорциях, построенные на математике, оптике, анатомии, становятся основой нового искусства. Они позволяли художнику создавать трехмерное пространство на плоскости, добиваться ощущения объёмности и рельефности предметов. Для некоторых мастеров многогранники являлись весьма удобной моделью для оттачивания мастерства изображения перспективы. Были и такие, кто искренне восхищался их симметрией и лаконичной красотой. Увлекался многогранниками и часто писал их на своих полотнах знаменитый Леонардо да Винчи (1452-1519). Он обогатил изображениями многогранников книгу своего друга монаха Луки Палочи (1445 – 1514) «О божественной пропорции».
Сальвадор Дали на картине «Тайная вечерня» изобразил Иисуса Христа со своими учениками на фоне огромного прозрачного додекаэдра.

В XIII-XVII вв. многогранники были основой архитектурных строений, больше всего применялись кубы, но по мере развития нашли применения и другие виды многогранников, такие как тетраэдр и октаэдр.

В наши дни многогранники – это главное открытие человечества. Мы в постоянном окружении многогранников: многие предметы быта имеют форму многогранников, все архитектурные строения возведены в стиле м ногогранных моделей.

Изготовление моделей многогранников.

Мы познакомились и воспользовались таким способом изготовления моделей многогранников, который называется методом развёрток.

Чаще всего при создании моделей многогранников из плоских разверток используют такие развертки, в

---

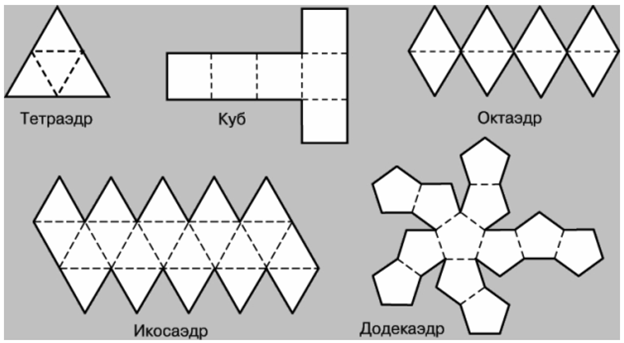
которых грани прилегают друг к другу ребрами, а модель строится путем загибания развертки вдоль ребер. Например, при создании моделей правильных многогранников чаще всего используют следующие развертки (Приложение 5)

Можно вырезать каждую грань отдельно, а затем склеить их в многогранник. Этот способ позволяет сэкономить расходный материал.









Кроме изготовления многогранников с помощью развёрток есть ещё и другие способы построения этих фигур. Это, например, изготовление Платоновых тел способом плетения, с помощью металлической проволоки или техники оригами. Эти способы позволяют создать удивительные по красоте конструкции.

Таким образом, мы создали коллекцию правильных многогранников, а некоторым из них нашли собственное практическое применение. Например, 12 граней додекаэдра можно использовать в качестве настольного календаря, а любой другой многогранник можно оформить в виде новогодней игрушки или в виде фотоальбома с различными темами содержания.

И вот что у нас получилось!





Опрос.

Кроме этого мы организовали выставку своих работ в классе и провели небольшой опрос в других классов.

• 
  Встречались ли Вы ранее с правильными многогранниками? Если - да, то где?
  
• 
  Эти фигуры вызывают Ваш интерес? Если - да, то какие именно?
  
• 
  Захотелось ли Вам самим попробовать изготовить их?
  
• 
  Как Вы думаете: где могут найти применение формы правильных многогранников?
  

Из 14 опрошенных почти все учащиеся встречались ранее с правильными многогранниками: в виде игрушек, сувениров, упаковок предметов, люстр, наглядных пособий в кабинете математики.

Всем участникам опроса понравились представленные фигуры, а многим понравились особенно те, которые ещё не были оформлены, так как им захотелось самим пофантазировать и придумать что-то своё с этими фигурами. Наибольший интерес вызвали додекаэдр (4 учащихся) и икосаэдр (5 учащихся) так они необычные и красивые и им хотелось бы научиться их изготавливать. Мы объяснили им как это сделать и что это совсем нетрудное и, главное, полезное занятие, потому, что развивается мелкая моторика рук, фантазия и творческие способности.

---

На вопрос где можно найти применение этим фигурам мы получили самые разнообразные ответы: кормушки для птиц, шкатулки, сувениры, украшения, и даже мебель.

Опрос показал, что правильные многогранники вызывают интерес, многим хочется заниматься таким творчеством, а самое главное – эти фигуры находят своё применение в учебной деятельности и в повседневной жизни.

Публикация в СМИ

В рамках взаимодействия со СМИ была написана статья и подобраны удачные фотографии, отражающие все этапы Урока творчества. Статья была напечатана на сайте ГУФСИН России по Свердловской области. (Приложение 6)

Заключение.

Мы познакомились с красивыми, совершенными и гармоничными фигурами - правильными многогранниками, узнали имена учёных, художников, которые посвятили этому свои труды. Ещё раз убедились, что истоки математики – в природе, в окружающей нас действительности.

Мы научились конструировать модели правильных многогранников, изучили историю возникновения, их свойства, нашли связь форм правильных многогранников с природными объектами, нашли применение в повседневной жизни. Мы убедились, что эти фигуры вызывают интерес у окружающих

Модели этих фигур могут найти применение на уроках физики, математики, химии, биологии как наглядно-иллюстративный материал, а так же, как материал для дальнейших исследований всех заинтересовавшихся.

Останавливаться на достигнутом нам бы не хотелось. В наших планах научиться изготовлять модели полуправильных и звёздчатых многогранников.

5. Список литературы и Интернет-ресурсов.

1. 
   Энциклопедический словарь юного математика. М., 1989.
   
2. 
   Смирнова И.М. В мире многогранников. М., 1990.
   
3. 
   Шарыгин И.Ф., Ерганжиева Л.Н. Наглядная геометрия. М., 1992.
   
4. 
   http://ru.wikipedia.org
   
5. 
   http://www.vseznaika.ru
   
6. 
   http://youtube.com
   
7. 
   http://origamisan.com
   
8. 
   http://liberte.com
   
9. 
   http://im0-tub-ru.yandex.net/i?id=ffb40eea69a705e84bc1650202023061&n=21
   
10. 
    http://im3-tub-ru.yandex.net/i?id=9cc09d8e342fa87d287ddaabca5d5bde&n=21
    

Приложение 1





Приложение 2

Характеристики правильных многогранников

Название многогранника	Вид	Число граней	Число вершин	Число ребер
Тетраэдр		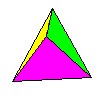4	4	6
Куб		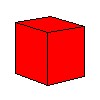6	8	12
Октаэдр		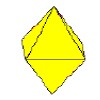8	6	12
Икосаэдр		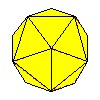20	12	30
Додекаэдр		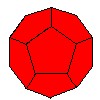12	20	30

---

Приложение 3

Использование форм стереометрических фигур в бытовых сферах.





Приложение 4







Приложение 5

Изготовление правильных многогранников


Приложение 6

Публикация в СМИ

---

Смотрите также файлы

• Способы формирования комолого стада для молочных комплексов ан. Елисеев, см. Коломийцев, В. А. Толкачёв, дн. Болдырев, нм. Наумов, де. Акульшина Аннотация.pdf

• Тренировка Present Simple Карточка 1.docx

• Дерево и Источник.doc

• Сильные стороны Слабые стороны.docx

• 24 лицейді 89сынып оушылары арасында 1 наурыз Алыс айту кніне арналан.docx