\Предмет: Геометрия

Дата: 28.11.2022

№ урока: 23

Класс: 10

Тема урока: «Расстояние от точки до плоскости»

Цели урока.

Дидактические:

– обобщить и систематизировать знания учащихся по теме;

–формировать умения и навыки по решению задач;

– стимулировать учащихся к овладению решением задач;

– проконтролировать степень усвоения знаний, умений и навыков по теме.

Развивающие:

– совершенствовать, развивать умения и навыки по решению задач на нахождение расстояния от точки до плоскости;

– развивать логическое мышление, учить анализировать и обобщать;

– продолжить работу по развитию математической речи и памяти.

Воспитательные:

– продолжить формирование навыков эстетического оформления записей в тетради и выполнения чертежей;

– приучать к умению общаться и выслушивать других;

– воспитание сознательной дисциплины;

– развитие творческой самостоятельности и инициативы.

Задачи урока:

• 
  Обеспечить усвоение новых понятий, изображать и определять на рисунке
  

перпендикуляр, наклонную, проекцию наклонной, расстояние от точки до плоскости

• 
  применить знания при решении задач базового уровня
  
• 
  развивать пространственное воображение;
  
• 
  развивать навыки, как самостоятельной деятельности, выслушивать объяснения и самому объяснять, проводить самоанализ своей работы.
  

Планируемые образовательные результаты:

предметные

• 
  знать определения понятий: перпендикуляр, наклонная, проекция;
  
• 
  знать план решения задачи
  

личностные

• 
  развитие познавательных интересов, учебных мотивов;
  
• 
  проявление дисциплинированности, трудолюбия и упорства в решении поставленных целей;
  

метапредметные

• 
  умение ставить перед собой цель и планировать деятельность в соответствии с поставленной целью;
  
• 
  сличение способа действия и его результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона;
  
• 
  умение вступать в сотрудничество с учителем и сверстниками, работать в группе;
  
• 
  формирование научного мировоззрения.
  

Применение нестандартных методов обучения

---

, ИКТ-технологий, повышает интерес к уроку, а, значит, и к математике в целом.

Дополнительное методическое и дидактическое обеспечение урока:

• 
  презентация к уроку;
  
• 
  карточки с задачами;
  
• 
  лист самооценки для каждого ученика
  

Содержание урока

1. 
   Организационный момент
   
2. 
   Актуализация опорных знаний. Проверка домашнего задания.
   
3. 
   Изучение нового материала
   
4. 
   Решение задач, закрепление материала
   
5. 
   Итог урока
   
6. 
   Рефлексия
   
7. 
   Домашнее задание
   

Ход урока

Содержание урока	Время (мин)	Деятельность
		Учителя	Учащихся
I этап. Организационный момент
Проверка готовности учащихся к началу урока Дорогие ребята! Сегодня мы с вами начнем работу по теме: “Расстояние от точки до плоскости”. Девизом сегодняшнего урока я выбрала слова знаменитого белорусского классика Якуба Колоса: “Только те знания становятся нашим достоянием, которые мы добываем сами”. На доске записана тема “Расстояние от точки до плоскости”. Цель нашего урока: узнать что же является расстоянием от точки до плоскости, научиться решать задачи по данной теме. На уроке нам понадобится хорошее настроение, внимательность, аккуратность и сообразительность (Учащиеся записывают в тетрадь дату, тему урока). В конце урока вы должны будете сами оценить свою работу.	2	Организационная Сообщает тему урока, дату проведения урока, цель урока	Сообщают об отсутствующих Записывают в тетради.
II этап. Актуализация опорных знаний. Проверка домашнего задания.
Ребята, давайте повторим основные теоретические знания по теме урока. Для успешной работы нам необходимо вспомнить определение, теоремы и формулы, которые понадобятся сегодня на уроке: определение прямой, перпендикулярной плоскости; признак перпендикулярности прямой и плоскости; теорема Пифагора; где лежит центр, описанной около треугольника окружности; (Ответы учащихся).	3	Учитель проводит фронтальный опрос по основным теоретическим вопросам темы.	Учащиеся отвечают на поставленные вопросы 1. Прямая называется перпендикулярной к плоскости если она перпендикулярна любой прямой лежащей в этой плоскости 2. Если прямая перпендикулярна к двум пересекающимся прямым лежащим в плоскости то она перпендикулярна и самой плоскости 3. Квадрат гипотенузы равен сумме квадратов катетов 4. На середине гипотенузы
III этап. Изучение нового материала
Объяснение ведется с помощью презентации, в результате на экране и в тетрадях учащихся появляются записи: (см. слайд 2,3)	10	Учитель объясняет материал, дает определения расстояния от точки до плоскости	Учащиеся записывают в тетрадь.
IV этап. Решение задач, закрепление материала
Решение задач: Задача: Доказать, что проекции равных наклонных, проведенных из одной точки равны. Обсудить вместе с классом алгоритм решения следующей задачи: (см. слайд 4, 5, 6) Найти расстояние от точки Р до плоскости треугольника, если точка Р равноудалена от его вершин. Вопросы к классу: -Что является расстоянием от точки до плоскости? -Где находится точка О ? -Каким свойством она обладает ? -От чего зависит местонахождение центра описанной окружности -Что нужно знать, чтобы найти искомое расстояние РА и РО, где РО- радиус описанной окружности) Составим план решения задачи: Определить тип треугольника и местонахождение точки о Сделать рисунок к задаче Найти радиус описанной окружности: Найти расстояние по теореме Пифагора: РО= (Решение задачи записывается на доске и в терадях) Решим задачу из учебника Л.С.Атанасяна «Геометрия 10-11» №150 К С Д Дано: АВСД - прямоугольник, АК ┴(АВС) КД=6см, КВ=7см, КС=9см. Найдите: ρ (К, (АВС)), ρ(АК, СД) Решение задачи см. в приложении1	10 10	Учитель решить задачу и оформить решение в тетради Задача №1 решается при помощи обсуждения, в результате должен быть выработан алгоритм решения задачи Направляет на верное рациональное решение, следит за верностью рассуждений учащихся	Учащиеся принимают активное участие во фронтальной беседе Предполагаемые ответы учащихся: 1.перпендикуляр 2. на прямой 3. она равноудалена от вершин треугольника, т.е. является центром описанной около треугольника окружности 4. от типа треугольника 5. воспользо-ваться теоремой Пифагора Предлагают способы решения. Один ученик записывает решение на доске.
V этап. Итог урока
Подведем итог урока, чтобы выяснить как вы усвоили новую тему выполним тест Тест. Решить тест, сдать работу Задания теста см.в приложении 2	7	Учитель раздает задания теста на карточках	Ученики вписывают ответы
VI этап. Рефлексия
Однажды Сократ, окруженный учениками, поднимался к храму. Навстречу им спускалась известная афинская гетера “Вот ты гордишься своими учениками, Сократ, - улыбнулась она ему, - но стоит мне только легонько поманить их, как они покинут тебя и пойдут вслед за мной”. Мудрец же ответил так: “Да, но ты зовешь их вниз, в теплую веселую долину, а я веду их вверх, к неприступным чистым вершинам”. Сегодня мы с вами поднялись еще на одну ступеньку вверх, и я хочу пожелать вам всегда добиваться поставленных целей.	3	Листы учета знаний находятся на парте у каждого ученика	Ученики заполняют
VII этап. Домашнее задание
§2. П.19 № 114, № 140. Д.п. Из точки S проведены на плоскость перпендикуляр SO и наклонные SAи SB. Длины наклонных соответственно равны 13 см и 20 см. Длина проекции наклонной AS равна 5 см. Найдите расстояние от точки S до плоскости и длину проекции наклонной SB.			Ученики записывают задания в дневник

---

Приложение 1



Приложение 2
Тест по теме «Расстояние от точки до плоскости».
1.Отрезок АН называется__перпендикуляром___________________,

проведенным из точки А к плоскости 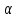, если прямая АН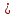 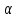и пересекает ее в точке Н. Точка Н – основание перпендикуляра______________________

2.Отрезок АМ называется __наклонной___________________________,

проведенной из точки А к плоскости 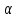, если прямая АМ не перпендикулярна плоскости 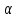и пересекает ее в точке М. Точка М – ___основание наклонной_

3. Перпендикуляр, проведенный из данной точки к плоскости, __меньше__________любой наклонной, проведенной из той же точки к этой плоскости.

4. Длина перпендикуляра, проведенного из точки А к плоскости 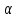называется _расстоянием от точки А к плоскости _________________

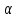5. Через точку М проведены прямые c и d , пересекающие плоскость 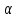в точках С и Д, причем прямая с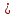 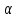. Тогда МС – _перпендикуляр______, МД – _____наклонная__________, СД – __проекция наклонной____________

6. Расстояние от точки А до плоскости 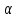равно 3 см. Длина перпендикуляра, проведенного из точки А к плоскости 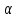равно _____3 см________.
7. Установите соответствие по рисунку.

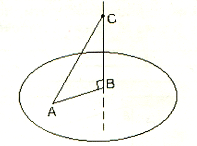
1. АС А. Проекция наклонной.

2. СВ В. Перпендикуляр.

---

3. АВ С. Наклонная.

Ответ: 1 __С__ 2 __В___ 3 ___А___

8. Из точки А к плоскости проведены наклонная АВ длиной 5 см. Найдите ее проекцию, если расстояние от точки до плоскости 3 см.

Ответ: _4 см.____

9. Расстояние между параллельными плоскостями – это расстояние _____расстояние от точки одной плоскости до другой_____________

10. Расстоянием между скрещивающимися прямыми называют __длину их общего перпендикуляра___________________________

11. Прямая NM параллельна плоскости . Расстоянием от точки N до плоскости равно 6 см. Расстояние от точки М до плоскости равно _ 6 см__

12. Точка В лежит в плоскости , а точка А находится от плоскости на расстоянии 8 см. Найдите расстояние от середины отрезка АВ до плоскости .

Ответ: 4 см.

---

Смотрите также файлы

• 2 12 4 3 Вставьте пропущенные гласные буквы в словах, чтобы получилось слово, относящееся к теме архитектура пк.docx

• Программа.docx

• Пояснительная записка содержит общую информацию о проекте. Эта часть документации должна использоваться при экспертизе проекта в целом и при оценке отдельных его фрагментов..pdf

• Ценообразование на маркетплейсе Основы ценообразования.pdf

• Лабораторная работа 3 по тосс (в 2х частях) Часть Резистивный усилитель на транзисторе Цель работы.doc