Файл: 638894001264428183.doc

5. Які існують способи вторинного групування:

1. побудова ряду розподілу;

2. перегрупування за кількома ознаками;

3. укрупнення інтервалів і перегрупування за питомою вагою груп у загальному підсумку;

4. перегрупування за одною ознакою.

6. Статистичне групування – це:

1. розподіл усієї сукупності на типи, групи за будь-якою істотною ознакою;

2. обробка і підрахунок групових і загальних підсумків статистичного спостереження;

3. обстеження і реєстрація окремих одиниць досліджуваного явища;

4. варіанта, яка є серединою впорядкованого варіаційного ряду;

7. Взаємопов’язані ознаки поділяють на:

1. факторні, структурні;

2. аналітичні, результативні;

3. факторні, результативні;

4. комбінаційні, структурні;

8. Полігон розподілу застосовують для зображення:

1. як дискретних, так і інтервальних варіаційних рядів;

2. зображення інтервальних варіаційних рядів;

3. дискретних варіаційних рядів.

9. У чому суть комбінаційного групування?

1. Групування за двома ознаками;

2. Групування за двома і більше ознаками;

3. Групування за однією ознакою;

4. Групування за кількома ознаками;

10. За допомогою якого виду графіків рядів розподілу зображуються інтервальні варіаційні ряди?

1. Полігон;

2. Гістограма;

3. Кумулята;

4. Огіва.

Практична робота №3

Тема: "Середні величини та показники варіації"

Мета роботи:З’ясувати сутність, значення, види середніх величин, показників варіації та методику їх розрахунку.

Завдання 1. На основі даних додатку визначити середню арифметичну просту, показники варіації. Зробити висновки.

Таблиця 1

Вихідні та розрахункові дані для визначення середньої арифметичної простої та показників варіації

1. На основі вихідних даних визначається середня площа за формулою

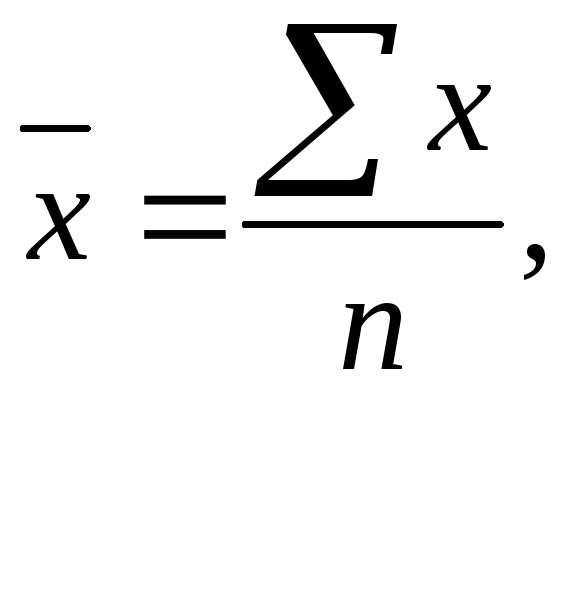
Де х – площа посіву культури, га;

n – кількість підприємств.

2. Розмах варіації:

3. Середнє лінійне відхилення просте:

.

4. Дисперсія проста:

σ²

5. Середнє квадратичне відхилення:

σ=

5. Коефіцієнт варіації:

Завдання 2. На основі додатку визначити:

1. Середню врожайність однієї із культур.

2. Дисперсію, середнє, лінійне, середнє квадратичне та коефіцієнт варіації врожайності.

Зробіть короткі висновки.

Таблиця 2

Вихідні та розрахункові дані для визначення середньої арифметичної зваженої та показників варіації

1. На основі вихідних і розрахункових даних визначається середня врожайність сільськогосподарських культур за середньою арифметичною зваженою:

Де - середня величина;

х – варіанти(врожайність);

ƒ – частота (посівна площа).

2. Розмір варіації:

3. Середнє лінійне відхилення зважене:

4. Дисперсія зважена:

5. Середнє квадратичне відхилення зважене:

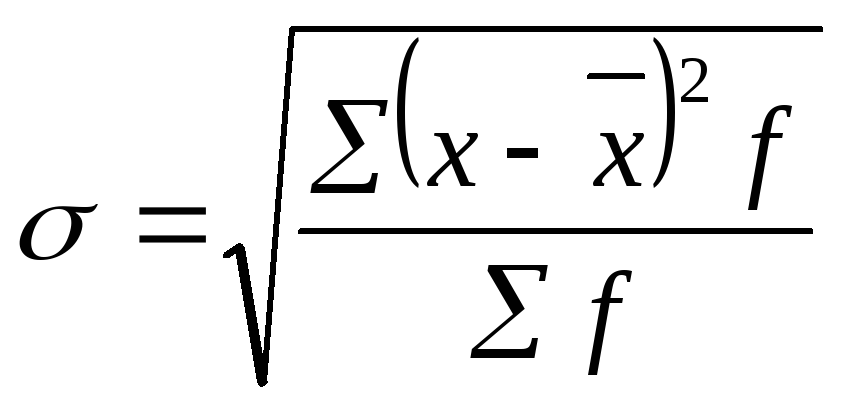
6. Коефіцієнт варіації

Завдання 3. На основі таблиці 3 розрахуйте середню врожайність сільськогосподарських культур за формулою середньої гармонічної зваженої:

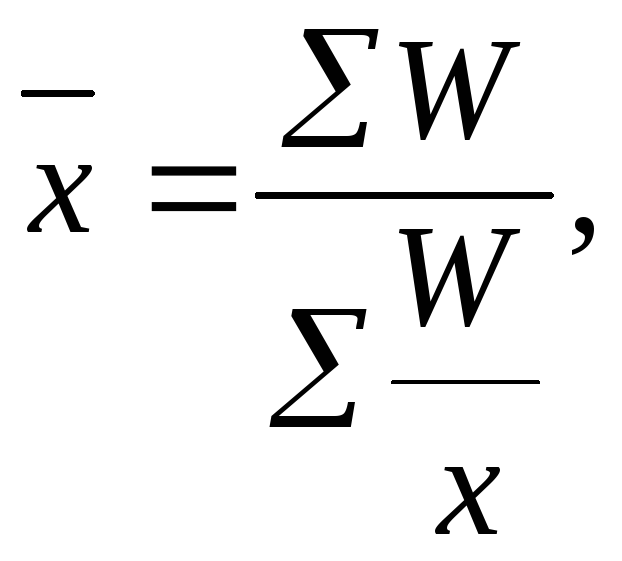
де W – валовий збір;

Х – врожайність.

Таблиця 3

Вихідні та розрахункові дані для визначення середньої гармонічної

Ключові терміни і поняття:

Варіація, варіаційний ряд розподілу, дисперсія, коефіцієнт варіації, медіана, мода, розмах варіації, середня величини , середня арифметична зважена, середня арифметична проста, середня гармонійна, середня хронологічна, ступеневі середні, частота, абсолютний показник, відносна величина.

Тестові завдання:

1. Варіація – це:

а) розподіл усієї сукупності на типи, групи за будь-якою істотною ознакою;

б) кількісна зміна величини досліджуваної ознаки в межах однорідної сукупності;

в) кількість одиниць спостереження, що мають однакове значення ознак;

г) графічне зображення рівня концентрації явища.

2. Мода-це:

а)варіанта, яка є серединою впорядковано-варіаційного ряду і ділить його на 2 рівні частини;

б)групування даних;

в)значення показника яке найчастіше зустрічається в сукупності;

г)відношення фактичного рівня показника до рівня, запланованого на той же період.

3. Медіана-це:

а)варіанта, яка є серединою впорядковано-варіаційного ряду і ділить його на 2 рівні частини;

б)групування даних;

в)значення показника яке найчастіше зустрічається в сукупності;

г)первинний елемент масового суспільного явища;

4. Розмах варіації – це:

1. різниця між найменшим і найбільшим значеннями варіюючої ознаки;

2. різниця між найбільшим і найменшим значеннями варіюючої ознаки;

3. відношення між між найбільшим і найменшим значеннями варіюючої ознаки;

4. відношення між найменшим і найбільшим значеннями варіюючої ознаки;

5. Знайти правильну відповідь до визначення абсолютних показників:

1. Показники, які відображають кількісні і якісні ознаки досліджуваних явищ;

2. Показники, які відображають кількісні ознаки певної сукупності;

3. Показники, які відображають розмір кількісних ознак досліджуваних явищ;

4. Показники, які відображають якісні ознаки певної сукупності;

6. Яка відносна величина характеризує співвідношення між складовими частинами цілого?

1. Відносна величина структури;

2. Відносна величина координації;

3. Відносна величина порівняння;

4. Відносна величина інтенсивності.

7. Середню гармонічну використовують:

1. тоді, коли загальний обсяг варіюючої ознаки для усієї сукупності становить суму індивідуальних значень усередненої ознаки;

2. для узагальненої характеристики тоді, коли відомі окремі значення досліджуваної ознаки і обсяги явищ, а частоти невідомі;

3. для узагальненої характеристики тоді, коли відомі окремі значення досліджуваної ознаки і обсяги явищ;

8. Коефіцієнт варіації можна розрахувати на основі:

а) середнього квадратичного відхилення;

б) середнього лінійного відхилення;

в) варіаційного розмаху;

г) середньої арифметичної зваженої.

9. Частотою називається :

1. окремі значення групувальної ознаки;

2. загальні значення групувальної ознаки;

3. кількість одиниць спостереження, що мають однакове значення ознаки;

10. В яких одиницях виражаються відносні показники, коли базова величина приймається за 1000?

1. У коефіцієнтах;

2. У процентах;

3. У проміле;

4. У продециміле;

11. Чому дорівнює алгебраїчна сума відхилень індивідуальних значень ознаки від середньої арифметичної?

1. Постійній величині;

2. Нулю;

3. Від'ємній величині;

4. Додатній величині.

Практична робота №4

Тема: "Кореляція"

Мета роботи: З’ясувати сутність, значення, область застосування кореляційного

аналізу.

Завдання 1. На основі даних підприємств побудуйте кореляційне поле, рівняння зв’язку та розрахуйте коефіцієнт кореляції, детермінації при прямолінійній залежності між ознаками. Проаналізуйте одержані результати.

Методика виконання:

При прямолінійній залежності парний кореляційний зв’язок між ознаками визначають за рівнянням прямої:

,

де - теоретичні значення результативної ознаки;

y - результативна ознака (урожайність);

x -факторна ознака (розмір затрат на 1 га);

a -початок відліку або значення y приx який дорівнює нулю;

b - коефіцієнт регресії рівняння зв’язку, який показує, як змінюється результативна

ознака залежно від зміни на одиницю факторної ознаки.

Дане рівняння можна розв’язувати способом найменших квадратів. Розв’язок рівняння зводиться до визначення невідомих параметрівa та b . Для їх визначення необхідно розв’язати систему двох нормальних рівнянь способом підстановки: