Файл: Курсач.docx

Изменчивость динамических структур данных предполагает не только изменения размера структуры, но и изменения связей между элементами. Для связных структур изменение связей не требует пересылки данных в памяти, а только изменения указателей в элементах связной структуры. В качестве примера приведена перестановка двух соседних элементов списка. В алгоритме перестановки в односвязном списке исходили из того, что известен адрес элемента, предшествующего паре, в которой производится перестановка. В приведенном алгоритме также не учитывается случай перестановки первого и второго элементов.

{==== Программный пример ====}

{ Перестановка двух соседних элементов в 1-связном списке }

Procedure ExchangeSll(

prev : sllptr { указатель на эл-т, предшествующий

переставляемой паре } );

var p1, p2 : sllptr; { указатели на эл-ты пары }

begin

p1:=prev^.next; { указатель на 1-й эл-т пары }

p2:=p1^.next; { указатель на 2-й эл-т пары }

p1^.next:=p2^.next; { 1-й элемент пары теперь указывает на

следующий за парой }

p2^.next:=p1; { 1-й эл-т пары теперь следует за 2-ым }

prev^.next:=p2; { 2-й эл-т пары теперь становится 1-ым }

end;

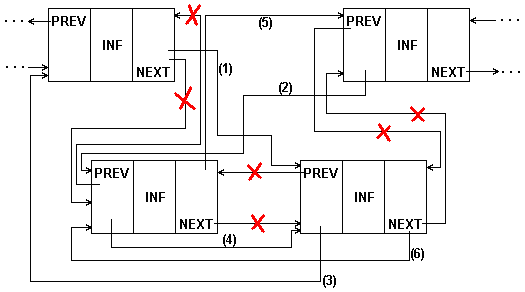
В процедуре перестановки для двухсвязного списка (рис.5.10.) нетрудно учесть и перестановку в начале/конце списка.

Копирование части списка.

При копировании исходный список сохраняется в памяти, и создается новый список. Информационные поля элементов нового списка содержат те же данные, что и в элементах старого списка, но поля связок в новом списке совершенно другие, поскольку элементы нового списка расположены по другим адресам в памяти. Существенно, что операция копирования предполагает дублирование данных в памяти. Если после создания копии будут изменены данные в исходном списке, то изменение не будет отражено в копии и наоборот.

Копирование для односвязного списка показано в программном примере.

{==== Программный пример ====}

{ Копирование части 1-связного списка. head - указатель на

начало копируемой части; num - число эл-тов. Ф-ция возвращает

указатель на список-копию }

Function CopySll ( head : sllptr; num : integer) : sllptr;

var cur, head2, cur2, prev2 : sllptr;

begin

if head=nil then { исходный список пуст - копия пуста }

CopySll:=nil

else begin

cur:=head; prev2:=nil;

{ перебор исходного списка до конца или по счетчику num }

while (num>0) and (cur<>nil) do begin

{ выделение памяти для эл-та выходного списка и запись в него

информационной части }

New(cur2); cur2^.inf:=cur^.inf;

{ если 1-й эл-т выходного списка - запоминается указатель на

начало, иначе - записывается указатель в предыдущий элемент }

if prev2<>nil then prev2^.next:=cur2 else head2:=cur2;

prev2:=cur2; { текущий эл-т становится предыдущим }

cur:=cur^.next; { продвижение по исходному списку }

num:=num-1; { подсчет эл-тов }

end;

cur2^.next:=nil; { пустой указатель - в последний эл-т

выходного списка }

CopySll:=head2; { вернуть указатель на начало вых.списка }

end; end;

Слияние двух списков.

Операция слияния заключается в формировании из двух списков одного - она аналогична операции сцепления строк. В случае односвязного списка, показанном в примере

слияние выполняется очень просто. Последний элемент первого списка содержит пустой указатель на следующий элемент, этот указатель служит признаком конца списка. Вместо этого пустого указатель в последний элемент первого списка заносится указатель на начало второго списка. Таким образом, второй список становится продолжением первого.

{==== Программный пример ====}

{ Слияние двух списков. head1 и head2 - указатели на начала

списков. На результирующий список указывает head1 }

Procedure Unite (var head1, head2 : sllptr);

var cur : sllptr;

begin { если 2-й список пустой - нечего делать }

if head2<>nil then begin

{ если 1-й список пустой, выходным списком будет 2-й }

if head1=nil then head1:=head2

else { перебор 1-го списка до последнего его эл-та }

begin cur:=head1;

while cur^.next<>nil do cur:=cur^.next;

{ последний эл-т 1-го списка указывает на начало 2-го }

cur^.next:=head2;

end; head2:=nil; { 2-й список аннулируется }

end; end;

Применение линейных списков

Линейные списки находят широкое применение в приложениях, где непредсказуемы требования на размер памяти, необходимой для хранения данных; большое число сложных операций над данными, особенно включений и исключений. На базе линейных списков могут строится стеки, очереди и деки. Представление очереди с помощью линейного списка позволяет достаточно просто обеспечить любые желаемые дисциплины обслуживания очереди. Особенно это удобно, когда число элементов в очереди трудно предсказуемо.

В программном примере показана организация стека на односвязном линейном списке. Стек представляется как линейный список, в котором включение элементов всегда производятся в начала списка, а исключение - также из начала. Для представления его нам достаточно иметь один указатель - top, который всегда указывает на последний записанный в стек элемент. В исходном состоянии (при пустом стеке) указатель top - пустой. Процедуры StackPush и StackPop сводятся к включению и исключению элемента в начало списка. Обратите внимание, что при включении элемента для него выделяется память, а при исключении - освобождается. Перед включением элемента проверяется доступный объем памяти, и если он не позволяет выделить память для нового элемента, стек считается заполненным. При очистке стека последовательно просматривается весь список и уничтожаются его элементы. При списковом представлении стека оказывается непросто определить размер стека. Эта операция могла бы потребовать перебора всего списка с подсчета числа элементов. Чтобы избежать последовательного перебора всего списка мы ввели дополнительную переменную stsize, которая отражает текущее число элементов в стеке и корректируется при каждом включении/исключении.

{==== Программный пример====}

{ Стек на 1-связном линейном списке }

unit Stack;

Interface

type data = ...; { эл-ты могут иметь любой тип }

Procedure StackInit;

Procedure StackClr;

Function StackPush(a : data) : boolean;

Function StackPop(Var a : data) : boolean;

Function StackSize : integer;

Implementation

type stptr = ^stit; { указатель на эл-т списка }

stit = record { элемент списка }

inf : data; { данные }

next: stptr; { указатель на следующий эл-т }

end;

Var top : stptr; { указатель на вершину стека }

stsize : longint; { размер стека }

{** инициализация - список пустой }

Procedure StackInit;

begin top:=nil; stsize:=0; end; { StackInit }

{** очистка - освобождение всей памяти }

Procedure StackClr;

var x : stptr;

begin { перебор эл-тов до конца списка и их уничтожение }

while top<>nil do

begin x:=top; top:=top^.next; Dispose(x); end;

stsize:=0;

end; { StackClr }

Function StackPush(a: data) : boolean; { занесение в стек }

var x : stptr;

begin { если нет больше свободной памяти - отказ }

if MaxAvail < SizeOf(stit) then StackPush:=false

else { выделение памяти для эл-та и заполнение инф.части }

begin New(x); x^.inf:=a;

{ новый эл-т помещается в голову списка }

x^.next:=top; top:=x;

stsize:=stsize+1; { коррекция размера }

StackPush:=true;

end;

end; { StackPush }

Function StackPop(var a: data) : boolean; { выборка из стека }

var x : stptr;

begin

{ список пуст - стек пуст }

if top=nil then StackPop:=false

else begin

a:=top^.inf; { выборка информации из 1-го эл-та списка }

{ 1-й эл-т исключается из списка, освобождается память }

x:=top; top:=top^.next; Dispose(top);

stsize:=stsize-1; { коррекция размера }

StackPop:=true;

end; end; { StackPop }

Function StackSize : integer; { определение размера стека }

begin StackSize:=stsize; end; { StackSize }

END.

Программный пример для организация на односвязном линейном списке очереди FIFI разработайте самостоятельно. Для линейного списка, представляющего очередь, необходимо будет сохранять: top - на первый элемент списка, и bottom - на последний элемент.

Линейные связные списки иногда используются также для представления таблиц - в тех случаях, когда размер таблицы может существенно изменяться в процессе ее существования. Однако, то обстоятельство, что доступ к элементам связного линейного списка может быть только последовательным, не позволяет применить к такой таблице эффективный двоичный поиск, что существенно ограничивает их применимость. Поскольку упорядоченность такой таблицы не может помочь в организации поиска, задачи сортировки таблиц, представленных линейными связными списками, возникают значительно реже, чем для таблиц в векторном представлении. Однако, в некоторых случаях для таблицы, хотя и не требуется частое выполнение поиска, но задача генерации отчетов требует расположения записей таблицы в некотором порядке. Для упорядочения записей такой таблицы применимы любые алгоритмы из описанных нами в разделе 3.9. Некоторые алгоритмы, возможно, потребуют каких-либо усложнений структуры, например, быструю сортировку Хоара целесообразно проводить только на двухсвязном списке, в цифровой сортировке удобно создавать промежуточные списке для цифровых групп и т.д. Мы приведем два простейших примера сортировки односвязного линейного списка. В обоих случаях мы предполагаем, что определены типы данных:

type lptr = ^item; { указатель на элемент списка }

item = record { элемент списка }

key : integer; { ключ }

inf : data; { данные }

next: lptr; { указатель на элемент списка }

end;

В обоих случаях сортировка ведется по возрастанию ключей. В обоих случаях параметром функции сортировки является указатель на начало неотсортированного списка, функция возвращает указатель на начало отсортированного списка. Прежний, несортированный список перестает существовать.

Указатель newh является указателем на начало выходного списка, исходно - пустого. Во входном списке ищется максимальный элемент. Найденный элемент исключается из входного списка и включается в начало выходного списка. Работа алгоритма заканчивается, когда входной список станет пустым. Обратим внимание читателя на несколько особенностей алгоритма. Во-первых, во входном списке ищется всякий раз не минимальный, а максимальный элемент. Поскольку элемент включается в начало выходного списка ,элементы с большими ключами оттесняются к концу выходного списка и последний, таким образом, оказывается отсортированным по возрастанию ключей. Во-вторых, при поиске во входном списке сохраняется не только адрес найденного элемента в списке, но и адрес предшествующего ему в списке эле- мента - это впоследствии облегчает исключение элемента из списка.

{==== Программный пример====}

{ Сортировка выборкой на 1-связном списке }

Function Sort(head : lptr) : lptr;

var newh, max, prev, pmax, cur : lptr;

begin newh:=nil; { выходной список - пустой }

while head<>nil do { цикл, пока не опустеет входной список }

begin max:=head; prev:=head; { нач.максимум - 1-й эл-т }

cur:=head^.next; { поиск максимума во входном списке }

while cur<>nil do begin

if cur^.key>max^.key then begin

{ запоминается адрес максимума и адрес предыдущего эл-та }

max:=cur; pmax:=prev;

end; prev:=cur; cur:=cur^.next; { движение по списку }

end; { исключение максимума из входного списка }

if max=head then head:=head^.next

else pmax^.next:=max^.next;

{ вставка в начало выходного списка }

max^.next:=newh; newh:=max;

end; Sort:=newh;

end;

В программном примере - иллюстрации сортировки вставками - из входного списка выбирается (и исключается) первый элемент и вставляется в выходной список "на свое место" в соответствии со значениями ключей.

{==== Программный пример ====}

{ Сортировка вставками на 1-связном списке }

type data = integer;

Function Sort(head : lptr) : lptr;

var newh, cur, sel : lptr;

begin

newh:=nil; { выходной список - пустой }

while head <> nil do begin { цикл, пока не опустеет входной список }